Coordenadas cilíndricas Sistema, mudança e exercícios

As Coordenadas cilíndricas Eles servem para localizar pontos no espaço tridimensional e consistem em uma coordenada radial ρ, uma coordenada azimutal φ e uma coordenada de altura z.

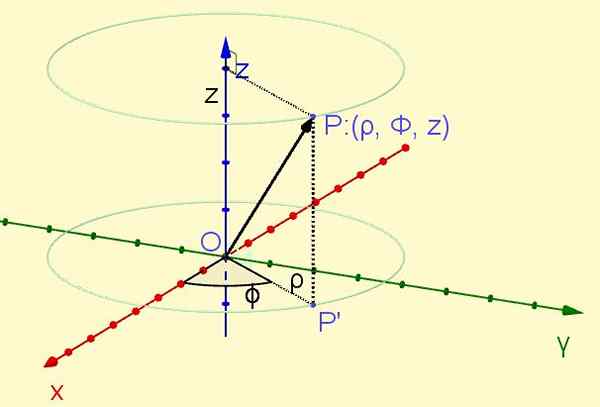
Um ponto P localizado no espaço é projetado ortogonalmente no avião XY dando origem ao ponto P ' Naquele avião. A distância da origem ao ponto P ' define a coordenada ρ, enquanto o ângulo que forma o eixo X Com a semi -forte Op ' Defina a coordenada φ. Finalmente, a coordenada z É a projeção ortogonal do ponto P no eixo Z. (Veja a Figura 1).

figura 1. Ponto P das coordenadas cilíndricas (ρ, φ, z). (Elaboração própria)

A coordenada radial ρ é sempre positiva, a coordenada azimutal φ varia de zero radianos a dois Pi Radianes, enquanto a coordenada Z pode assumir qualquer valor real:

0 ≤ ρ < ∞

0 ≤ φ < 2π

- ∞ < z < + ∞

[TOC]

Mudança de coordenadas

É relativamente simples obter as coordenadas cartesianas (x, y, z) de um ponto P de suas coordenadas cilíndricas (ρ, φ, z):

x = ρ cos (φ)

y = ρ sen (φ)

z = z

Mas também é possível obter as coordenadas polares (ρ, φ, z) com base no conhecimento das coordenadas cartesianas (x, y, z) de um ponto P:

ρ = √ (x² + e²)

φ = arctan (y/x)

z = z

Base vetorial em coordenadas cilíndricas

A base dos vetores cilíndricos é definida Uρ, Uφ, Uz.

O vetor Uρ É tangente à linha φ = ctte e z = ctte (apontando radialmente para fora), o vetor Uφ é tangente à linha ρ = ctte e z = ctte e finalmente Uz Tem a mesma direção do eixo z.

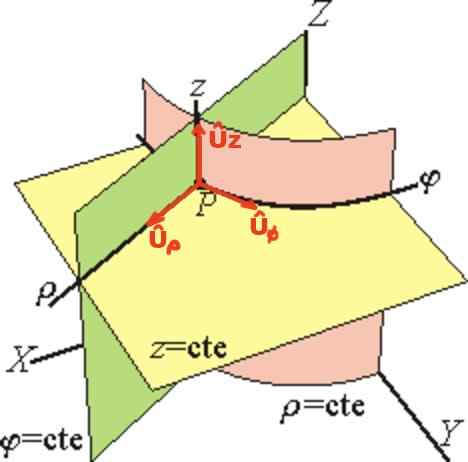Figura 2. Base de coordenadas cilíndricas. (Wikimedia Commons)

Na base da unidade cilíndrica, o vetor de posição r De um ponto P, está escrito vetorialmente assim:

Pode servir a você: domínio e contradição de uma função (com exemplos)

r = ρ Uρ + 0 Uφ + z Uz

Por outro lado, um deslocamento infinitesimal Dr Do ponto P, é expresso o seguinte:

dr = Dρ Uρ + ρ dφ  Uφ + Dz Uz

Da mesma forma, um elemento infinitesimal do volume de DV em coordenadas cilíndricas é:

Dv = ρ dρ dφ dz

Exemplos

Existem inúmeros exemplos do uso e aplicação de coordenadas cilíndricas. Na cartografia, por exemplo, o Projeção cilíndrica, baseado com precisão nessas coordenadas. Existem mais exemplos:

Exemplo 1

Coordenadas cilíndricas têm aplicações em tecnologia. Como exemplo, você tem o sistema CHS (setor da cabeça do cilindro) de localização de dados em um disco rígido, que realmente consiste em vários discos:

- O cilindro ou faixa corresponde a coordenar ρ.

- O setor corresponde à posição φ do álbum que gira em alta velocidade angular.

- A cabeça corresponde à posição Z da cabeça de leitura no álbum correspondente.

Cada byte de informação tem um endereço preciso nas coordenadas cilíndricas (C, S, H).

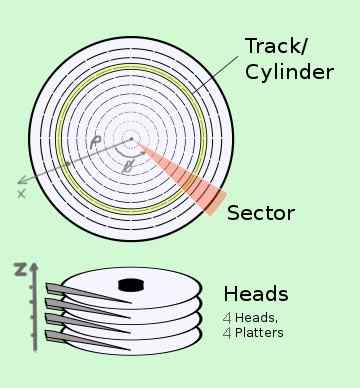Figura 2. Localização da informação em coordenadas cilíndricas em um sistema de disco rígido. (Wikimedia Commons)

Exemplo 2

Guindastes de construção definem a posição de carga nas coordenadas cilíndricas. A posição horizontal é definida pela distância do eixo do guindaste ou seta. A posição vertical da carga é determinada pela coordenada z da altura.

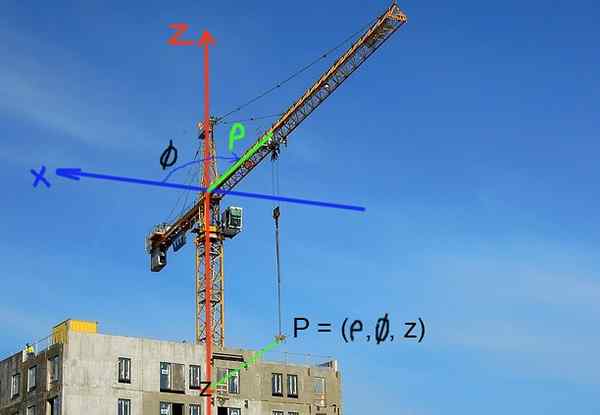Figura 3. A posição da carga em um guindaste de construção pode ser facilmente expressa em coordenadas cilíndricas. (Imagem Pixabay - RCOS R. Pérez)

Exercícios resolvidos

Exercício 1

Existem os pontos P1 das coordenadas cilíndricas (3, 120º, -4) e o ponto P2 de coordenadas cilíndricas (2, 90º, 5). Encontre o Distância euclidiana Entre esses dois pontos.

Pode atendê -lo: divisões em que o resíduo é 300

Solução: Primeiro, passamos a encontrar as coordenadas cartesianas de cada ponto seguindo a fórmula que ocorreu acima.

P1 = (3* cos 120º, 3* sen 120º, -4) = (-1.5, 2.60, -4)

P2 = (2* cos 90º, 2* sin 90º, 5) = (0, 2, 5)

A distância euclidiana entre P1 e P2 é:

D (p1, p2) = √ ((0 - (-1.5))²+(2 - 2.60)²+(5 -(-4))² ) =…

… √ (2.25+0.36+81) = 9.14

Exercício 2

O ponto P tem coordenadas cartesianas (-3, 4, 2). Encontre as coordenadas cilíndricas correspondentes.

Solução: As coordenadas cilíndricas são encontradas usando os relacionamentos dados acima:

ρ = √ (x² + e²) = √ (-3)² + 4²) = √ (9 + 16) = √ (25) = 5

φ = arctan (y/x) = arcan (4/(-3)) = -53.13º + 180º = 126.87º

Z = 2

Deve -se lembrar que a função arcangente é multivaluada de periodicidade 180º. Além disso, o ângulo φ deve pertencer ao segundo quadrante, uma vez que os x e y e as coordenadas do ponto P estão nesse quadrante. Esta é a razão pela qual 180º foram adicionados ao resultado φ.

Exercício 3

Expresso em coordenadas cilíndricas e em coordenadas cartesianas a superfície de um cilindro de rádio 2 e cujo eixo coincide com o eixo z.

Solução: entende -se que o cilindro tem uma extensão infinita na direção z, de modo que a equação da referida superfície nas coordenadas cilíndricas é:

ρ = 2

Para obter a equação cartesiana da superfície cilíndrica, o quadrado de ambos os membros da equação anterior é tomado:

ρ² = 4

Multiplamos por 1 ambos os membros da igualdade anterior e aplicamos o Identidade trigonométrica fundamental (Sen²(φ) + cos²(φ) = 1):

1 * ρ² = 1 * 4

(Sen²(φ) + cos²(φ)) * ρ² = 1 * 4

O parêntese se desenvolve para obter:

(ρ sen (φ))² + (ρ cos (φ))² = 4

Pode atendê -lo: população e amostra

Lembramos que a primeira parêntese (ρ sen (φ)) é coordenada e um ponto nas coordenadas polares, enquanto o parêntese (ρ cos (φ)) representa a coordenada X, de modo que nos deixamos A equação do cilindro em coordenadas cartesianas:

e² + x² = 2²

A equação anterior não deve ser confundida com a de um círculo no plano XY, pois neste caso seria assim: e² + x² = 2² ; Z = 0.

Exercício 4

Um cilindro de raio r = 1 me altura h = 1m tem sua massa radialmente distribuída de acordo com a seguinte equação d (ρ) = c (1 - ρ/r) onde c é uma constante de valor c = 1 kg/m³. Encontre a massa total do cilindro em quilogramas.

Solução: A primeira coisa é perceber que a função d (ρ) representa a densidade de massa volumétrica e que a massa de densidade é distribuída em cascaronas cilíndricas de densidade decrescente do centro à periferia. Um elemento infinitesimal de volume de acordo com a simetria do problema é:

Dv = ρ dρ 2π h

A partir daí, você precisa, a massa infinitesimal de uma concha cilíndrica será:

Dm = D (ρ) DV

Portanto, a massa total do cilindro será expressa pelo seguinte Integral definido:

M = ∫_qualquer^R D (ρ) dv = ∫_qualquer^R C (1 - ρ/r) ρ dρ 2π h = 2π h c ∫_qualquer^R (1 - ρ/r) ρ dρ

A solução da integral indicada não é difícil de obter, sendo seu resultado:

∫_qualquer^R (1 - ρ/r) ρ dρ = (⅙) r²

Incorporando esse resultado na expressão da massa do cilindro é obtida:

M = 2π h c (⅙) r² = ⅓ π h c r² =

 ⅓ π 1m*1kg/m³* 1M² = π/3 kg ≈ 1.05 kg

Referências

1. Arfken G e Weber H. (2012). Métodos matemáticos para físicos. Um guia abrangente. 7ª edição. Academic Press. ISBN 978-0-12-384654-9
2. Cálculo do CC. Coordenadas cilíndricas e esféricas resolvidas. Recuperado de: cálculo.DC
3. Weisstein, Eric W. “Coordenadas cilíndricas.”De Mathworld-A Wolfram Web. Recuperado de: Mathworld.Volfrâmio.com
4. Wikipedia. Sistema de coordenadas cilíndricas. Recuperado de: em.Wikipedia.com
5. Wikipedia. Campos vetoriais em coordenadas cilíndricas e esféricas. Recuperado de: em.Wikipedia.com