Figuras congruentes, critérios, exemplos, exercícios

O congruência, Na geometria, ele ressalta que, se duas figuras planas tiverem a mesma forma e dimensões, estes são congruentes. Por exemplo, dois segmentos são congruentes quando seus comprimentos são iguais. Além disso, os ângulos congruentes têm a mesma medida, embora não sejam orientados da mesma maneira no avião.

O termo "congruência" vem do latim Congruentia, cujo significado é correspondência. Assim, duas figuras congruentes correspondem exatamente uma com a outra.

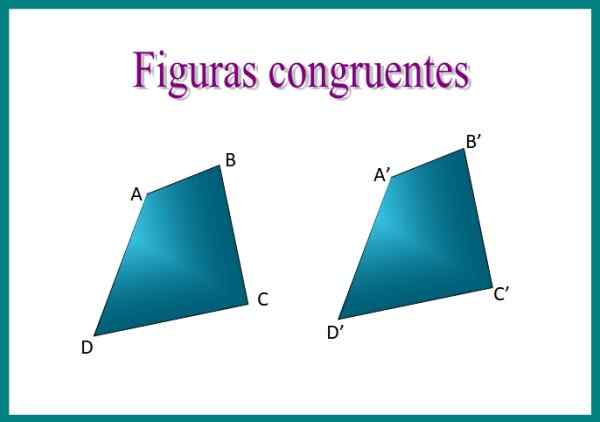
figura 1. Os quadrilásteros abcd e a'b'c'd 'da figura são congruentes: seus lados têm a mesma medida, bem como seus ângulos internos. Fonte: f. Zapata.

Por exemplo, se sobrepormos os dois quadriláteros da imagem, descobriremos que eles são congruentes, uma vez que a disposição de seus lados é idêntica e eles medem o mesmo.

Ao colocar os quadrilaterais abcd e a'b'c'd 'em outro, os números coincidirão exatamente. Os lados correspondentes são chamados lados homólogos qualquer correspondente E para expressar a congruência, o símbolo é usado. Então podemos dizer que abcd ≡ a'b'c'd '.

[TOC]

Critérios de congruência

As seguintes características são comuns a polígonos congruentes:

-Igual forma e tamanho.

-Medidas idênticas de seus ângulos.

-A mesma extensão em cada um de seus lados.

No caso de dois polígonos em questão serem regulares, ou seja, que todos os lados e ângulos internos medem o mesmo, a congruência é garantida quando uma das seguintes condições é atendida:

-Os lados são congruentes

-As Apotemas tem a mesma medida

-Ele rádio de cada polígono mede o mesmo

O apoteme de um polígono comum é a distância entre o centro e um dos lados, enquanto o raio corresponde à distância entre o centro e um vértice ou canto da figura.

Os critérios de congruência são frequentemente usados ​​porque muitas partes e peças de todos os tipos são fabricadas em série e devem ter a mesma forma e medidas. Dessa forma, eles podem ser facilmente substituídos quando necessário, por exemplo, nozes, parafusos, folhas ou pedras do chão na rua.

Pode atendê -lo: Simpson Regra: Fórmula, Demonstração, Exemplos, ExercíciosFigura 2. Os paralelepípedos da rua são figuras congruentes, uma vez que sua forma e dimensões são exatamente as mesmas, embora sua orientação no chão possa mudar. Fonte: Pixabay.

Congruência, identidade e similaridade

Existem conceitos geométricos relacionados à congruência, por exemplo As figuras idênticas e as figuras semelhantes, isso não implica necessariamente que os números sejam congruentes.

Observe que os números congruentes são idênticos, no entanto, os quadriláteros da Figura 1 podem ser orientados de maneiras diferentes no plano e ainda continuarem congruentes, uma vez que a orientação diferente não muda o tamanho de seus lados ou o de seus ângulos. Nesse caso, eles deixariam de ser idênticos.

O outro conceito é o da semelhança das figuras: duas figuras planas são semelhantes se tiverem a mesma forma e seus ângulos internos medem iguais, embora o tamanho das figuras possa ser diferente. Se for esse o caso, os números não são congruentes.

Exemplos de congruência

- Congruência de ângulos

Como indicamos no início, os ângulos congruentes têm a mesma medida. Existem várias maneiras de obter ângulos congruentes:

Exemplo 1

Duas linhas com um ponto comum definem dois ângulos, chamados Ângulos opostos pelo vértice. Esses ângulos têm a mesma medida, portanto são congruentes.

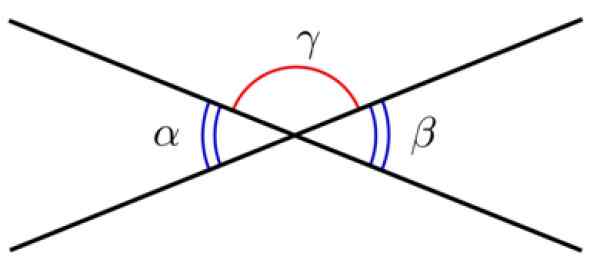Figura 3. Ângulos opostos pelo vértice. Fonte: Wikimedia Commons.

Exemplo 2

Existem duas linhas paralelas mais uma linha t que cruza os dois. Como no exemplo anterior, quando essa linha cruza os paralelos, gera ângulos congruentes, um em cada linha para o lado direito e outros dois no lado esquerdo. A figura mostra α e α₁, À direita da linha t, Eles são congruentes.

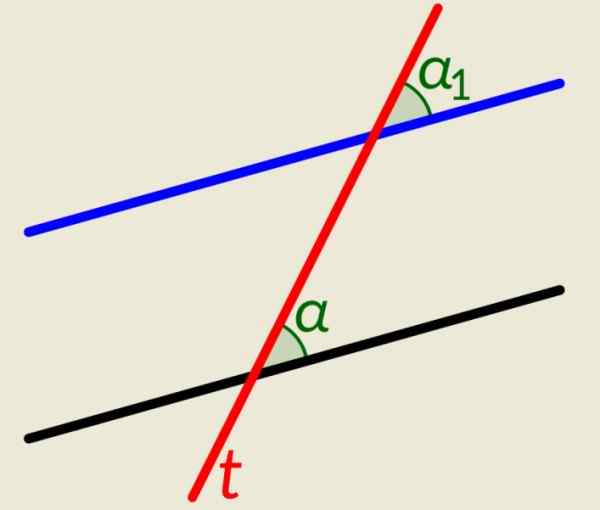Figura 4. Os ângulos mostrados na figura são congruentes. Fonte: Wikimedia Commons. Lfahlberg/CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0).

Exemplo 3

Em um paralelogramo, existem quatro ângulos internos, que são congruentes dois a dois. Eles são aqueles entre vértices opostos, como mostrado na figura a seguir, na qual os dois ângulos verdes são congruentes, bem como os dois ângulos em vermelho.

Pode atendê -lo: Acutangle Triangle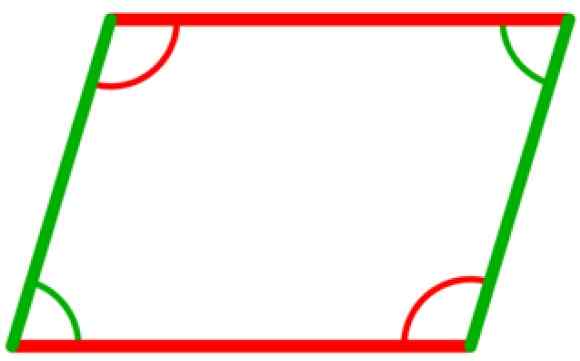Figura 5. Os ângulos internos do paralelogramo são congruentes dois a dois. Fonte: Wikimedia Commons.

- Congruência de triângulos

Dois triângulos de forma idêntica e o mesmo tamanho são congruentes. Para verificar isso, existem três critérios que podem ser examinados em busca de congruência:

-Critérios da LLL: Os três lados dos triângulos têm as mesmas medidas, portanto l₁ = L '₁; eu₂ = L '₂ e eu₃ = L '_3.

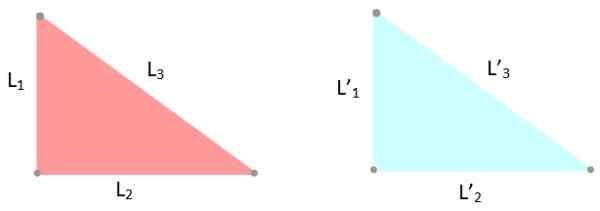Figura 6. Exemplo de triângulos congruentes, cujos lados medem iguais. Fonte: f. Zapata.

-Critérios alla y aal: Os triângulos têm dois ângulos internos iguais e o lado entre esses ângulos tem a mesma medida.

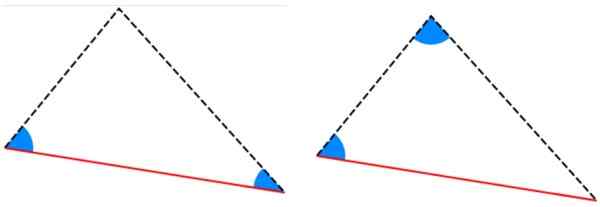Figura 7. Critérios Ala e Aal por congruência de triângulos. Fonte: Wikimedia Commons.

-Critérios lal: Dois dos lados são idênticos (correspondentes) e, entre eles.

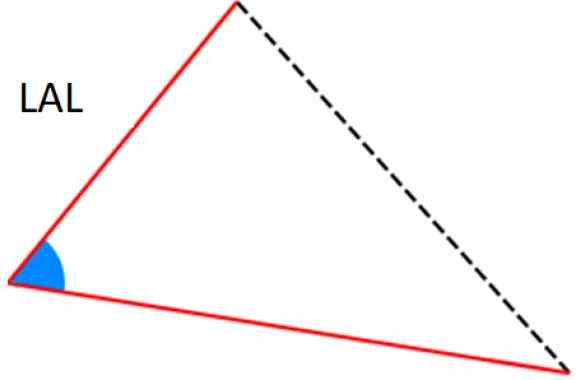Figura 8. Critérios lal para congruência de triângulos. Fonte: Wikimedia Commons.

Exercícios resolvidos

- Exercício 1

Na Figura seguinte, os triângulos são mostrados: ΔABC e ΔECF. Sabe -se que ac = ef, que ab = 6 e que cf = 10. Além disso, os ângulos ∡bac e ∡fec são congruentes e os ângulos ∡acb e ∡fcb também são.

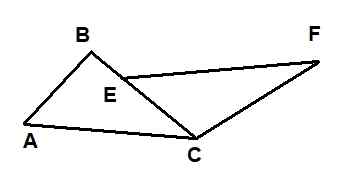Figura 9. Triângulos para o exemplo resolvido 1. Fonte: f. Zapata.

Então o comprimento do segmento be é igual a:

(i) 5 

(Ii) 3

(Iii) 4 

(Iv) 2

(v) 6

Solução

Como os dois triângulos têm um lado de igual comprimento ac = ef entre os ângulos iguais ∡bac = ∡cef e ∡bca = ∡cfe, pode -se dizer que os dois triângulos são congruentes pela asa dos critérios.

Isso é Δbac ≡ Δcef, então você precisa:

Ba = ce = ab = 6

BC = cf = 10

AC = ef

Mas o segmento que você deseja calcular é = BC - EC = 10 - 6 = 4.

Para que a resposta correta seja (iii).

- Exercício 2

Três triângulos são mostrados na figura. Sabe -se também que os dois ângulos indicados medem 80º cada e que os segmentos AB = PD e AP = CD. Encontre o valor do ângulo X indicado na figura.

Pode atendê -lo: gráficos polybal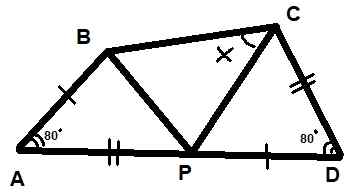Figura 10. Triângulos para o exemplo resolvido 2. Fonte: f. Zapata.

Solução

Você deve aplicar as propriedades dos triângulos, que são detalhados passo a passo.

Passo 1

Começando com os critérios de congruência dos triângulos de LAL, pode -se dizer que os triângulos BAP e PDC são congruentes:

ΔBAP ≡ ΔPDC

Passo 2

O acima leva a afirmar que BP = PC, portanto, o triângulo ΔBPC é isosceles e ∡pcb = ∡pbc = x.

etapa 3

Se ligarmos para γ no ângulo do BPC, segue -se que:

2x + γ = 180º

Passo 4

E se ligarmos para β para os ângulos APB e DCP e α para os ângulos ABP e DPC, ele deve::

α + β + γ = 180º (já que APB é um ângulo plano).

Etapa 5

Além disso, α + β + 80º = 180º por soma de ângulos internos do triângulo APB.

Etapa 6

Combinando todas essas expressões que você precisa:

α + β = 100º

Etapa 7

E, por conseguinte:

γ = 80º.

Etapa 8

Finalmente segue isso:

2x + 80º = 180º

Com x = 50º.

Referências

1. Baldor, a. 1973.Geometria plana e espacial. Cultural da América Central.
2. Fundação CK-12. Polígonos congruentes. Recuperado de: CK 12.org.
3. Desfrute de matemática. Definições: rádio (polígono). Recuperado de: desfrutar.com.
4. Math Open Reference. Testando polígonos para congruência. Recuperado de: MathpenRef.com.
5. Wikipedia. Congruência (geometria). Recuperado de: é.Wikipedia.org.
6. Zapata, f. Triângulos, história, elementos, classificação, propriedades. Recuperado de: Lifer.com.