Conceito de compressão e fórmulas, cálculo, exemplos, exercícios

O esforço de compressão ou compressão É a força por unidade de área cujo resultado é empurrar, apertar ou comprimir um objeto, tendendo a encurtar. Matematicamente é:

E = f /a

Aqui E Denot o esforço, F a magnitude da força e PARA A área em que a unidade está no sistema internacional se o Newton/M² Ó Pascal (PA). O esforço de compressão é um esforço normal, Porque a força que o produz é perpendicular à área sobre a qual é exercida.

figura 1. As colunas na acrópole de Atenas estão sujeitas a compressão. Fonte: Pixabay.

Esse esforço pode comprimir o objeto ou pelo contrário, apertar e esticá -lo, conforme aplicado. No caso do esforço de compressão, as forças se aplicam na direção oposta para exercer o efeito de apertar e diminuir o objeto.

Uma vez que as forças cessam, muitos materiais retornam às suas dimensões originais. Esta propriedade é conhecida pelo nome de elasticidade. Mas enquanto isso acontecer, a deformação elástica unitária sofrida por um material sujeito a um esforço é:

Deformação unitária = (tamanho final - tamanho inicial)/tamanho inicial

A deformação pode ser linear, superficial ou volume, embora a deformação unitária não tenha unidades. No entanto, as informações que ele fornece são muito importantes, pois não é a mesma para deformar uma barra de 10 m de comprimento em 1 cm, para deformar 1 cm de outra barra de 1 m de comprimento.

Em um material elástico, a deformação e o esforço são proporcionais, cumprindo a lei de Hooke:

Esforço ∝ Deformação unitária

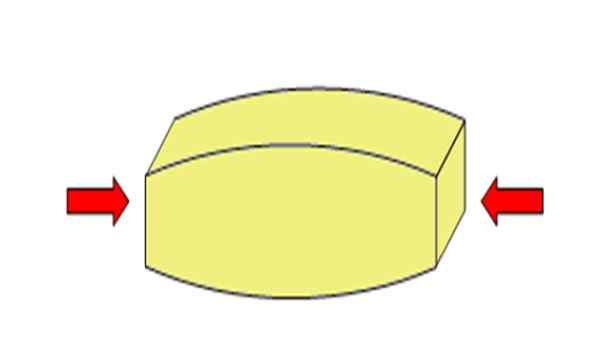Figura 2. O esforço de compressão diminui a duração do objeto. Fonte: Wikimedia Commons. Adre-es [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenças/BY-SA/4.0)].[TOC]

¿Como calcular a compressão?

O esforço de compressão faz com que as partículas do material se aproximem e mais, reduzindo seu tamanho. Dependendo da direção em que o esforço é aplicado, haverá uma redução ou redução em qualquer uma de suas dimensões.

Pode atendê -lo: modelo mecânico quântico do átomo

Vamos começar assumindo uma barra fina de comprimento original eu,  ao qual o esforço normal de magnitude é aplicado E. Se o esforço é compressão, o bar sofre uma redução em seu comprimento, denotada por δ. Se for tensão, a barra será estendida.

Naturalmente, o material do qual o elemento é feito é decisivo em sua capacidade de apoiar os esforços.

Essas características elásticas do material são incluídas na constante de proporcionalidade acima mencionada. Se chama Módulo de elasticidade qualquer Módulo jovem e é indicado como e. Cada material possui um módulo de elasticidade, que é determinado experimentalmente através de testes de laboratório.

Com isso em mente, o esforço E É expresso de maneira matemática assim:

Esforço ∝ Deformação unitária

Finalmente, para estabelecer essa condição como uma equação, é necessária uma constante de proporcionalidade para substituir o símbolo da proporcionalidade ∝ e substituí -la por igualdade, assim:

Esforço = proporcionalidade constante x deformação da unidade        

E = y. (Δ /L)

O quociente (Δ /L) É a deformação unitária, indicada como ε e com δ = Comprimento final - comprimento inicial. Dessa forma, o esforço E Permanece como:

E = y. ε

Como a deformação da unidade não tem dimensão, as unidades de E são os mesmos que os de E: N/m² ou PA no sistema SI, libras/em² o psi no sistema britânico, bem como outras combinações de força e área, como kg/cm².

Módulo de elasticidade de diferentes materiais

Os valores de e são determinados experimentalmente no laboratório, em condições controladas. Em seguida, o módulo de elasticidade para materiais amplamente utilizado na construção e também o dos ossos:

Pode atendê -lo: vetores no espaço: como representar graficamente, aplicações, exercícios

tabela 1

Material	Módulo de elasticidade Y (PA) x 109
Aço	200
Ferro	100
Latão	100
Bronze	90
Alumínio	70
Mármore	cinquenta
Granito	Quatro cinco
Concreto	vinte
Osso	quinze
Pinhal	10

Exemplos

Os esforços de compressão atuam em várias estruturas; O mesmo que está sujeito à ação de forças como o peso de cada um dos elementos que os compõem, bem como forças de agentes externos: vento, neve, outras estruturas e mais.

É comum que a maioria das estruturas seja projetada para resistir aos esforços de todos os tipos sem se deformar. Portanto, é necessário levar em consideração o esforço de compressão para impedir que a peça ou o objeto perca sua forma.

Além disso, os ossos do esqueleto são estruturas sujeitas a vários esforços. Embora os ossos sejam resistentes a eles, quando o limite elástico é excedido por acidente, fissuras e fraturas originam.

Colunas e pilares

As colunas e pilares dos edifícios devem ser feitos para resistir à compressão, caso contrário, eles tendem a arquear. Isso é conhecido como Flexão lateral qualquer flambagem.

As colunas (veja a Figura 1) são elementos cujo comprimento é muito maior em comparação com a área de sua seção transversal.

Um elemento cilíndrico é uma coluna quando seu comprimento é igual ou superior a dez vezes o diâmetro da seção transversal. Mas se a seção transversal não for constante, seu diâmetro menor será tomado com o objetivo de classificar o elemento como uma coluna.

Cadeiras e bancos

Quando as pessoas se sentam em móveis, como cadeiras e bancos, ou adicionam objetos por cima, as pernas estão sujeitas a esforços de compressão que tendem a reduzir sua altura.

Figura 3. Ao sentar, as pessoas exercem um esforço de compressão na cadeira, que tende a diminuir sua altura. Fonte: Pixabay.

Normalmente, os móveis são feitos para resistir ao peso muito bem e retornar ao seu estado natural quando for removido. Mas se um ótimo peso for colocado em cadeiras ou bancos frágeis, as pernas cedem à compressão e quebra.

Pode atendê -lo: condutores elétricos

Exercícios

- Exercício 1

Você tem uma haste que mede originalmente 12 m de comprimento, a que passa por um esforço de compressão, de modo que sua deformação unitária seja -0.0004. Qual é o novo comprimento da haste?

Solução

A partir da equação dada acima:

ε = (Δ /L) = - 0.0004

Sim eu_F É a duração final e eu_qualquer a duração inicial, já Δ = L_F - eu_qualquer  se tem:

(EU_F - eu_qualquer)/ EU_qualquer = -0.0004

Portanto: eu_F - eu_qualquer = -0.0004 x 12 m = -0.0048 m. E finalmente:

eu_F  = (12 - 0.0048) M = 11.9952 m.

- Exercício 2

Uma barra de aço sólido, cilíndrica, mede 6 m de comprimento e 8 cm de diâmetro. Se a barra for submetida a compressão por meio de uma carga de 90.000 kg, encontre:

a) A magnitude do esforço de compressão em megapascal (MPA)

b) Quanto a duração da barra diminuiu?

Solução para

Primeiro é a área A da seção transversal da barra, que depende do seu diâmetro D, resultando em:

A = π. D² / 4 = π. (0.08 m)² / 4 = 5.03 x 10^-3 m²

A força é imediatamente, através de F = m.G = 90.000 kg x 9.8 m/s²= 882.000 n.

Finalmente, o esforço médio é calculado da seguinte maneira:

E = f/ a = 882.000 N/ 5.03 x 10^-3 m² = 1.75 x 10⁸ PA = 175 MPA

Solução b

A equação para o esforço agora é usada, sabendo que o material tem resposta elástica:

E = y. (Δ /L)

O módulo jovem de aço é encontrado na Tabela 1:

Δ = e.L / y = 6 m x 1.75 x 10⁸ PA / 200 x 10 ⁹ PA = 5.25 x 10 ^-3 M = 5.25 mm.

Referências

1. Cerveja, f. 2010. Mecânica de Materiais. 5 ª. Edição. McGraw Hill.
2. Giancoli, d.  2006. Física: Princípios com aplicações. 6^TTH  Ed. Prentice Hall.
3. Hibbeler, R.C. 2006. Mecânica de Materiais. 6º. Edição. Pearson Education.
4. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. McGraw Hill
5. Wikipedia. Estresse (mecânica). Recuperado de: Wikipedia.org.