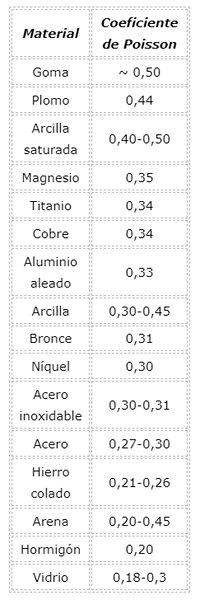
Coeficiente de Poisson Coeficiente, fórmulas, valores, exemplos

Ele Coeficiente de Poisson É uma quantidade adimensional, característica de cada material. É um indicativo da deformação de um pedaço de material antes da aplicação de certos esforços.

Quando uma peça material que sofre tensão, ou compressão, sofre uma deformação, o quociente entre deformação transversal e deformação longitudinal é precisamente o coeficiente de Poisson.

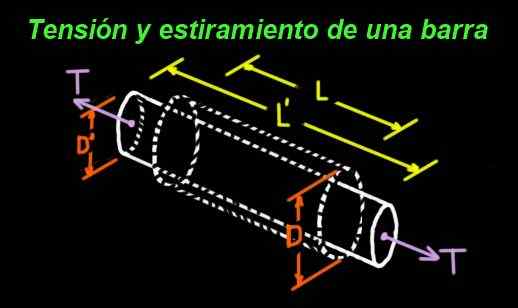
figura 1. O coeficiente de Poisson mede a relação entre alongamento longitudinal e estreitamento transversal. (Preparado por Ricardo Pérez)

Por exemplo, um cilindro de borracha que sofre tensão nas extremidades é esticado na direção longitudinal, mas é transversalmente estreita. A Figura 1 mostra uma barra cujas dimensões originais são: L longo e diâmetro D.

A barra é submetida a uma tensão T por suas extremidades e, como conseqüência dessa tensão, sofre um trecho, de modo que o novo comprimento seja l '> l. Mas, ao alongar, um estreitamento de seu diâmetro também ocorre com o novo valor: D ' < D.

O quociente entre alongamento (positivo) e estreitamento (negativo) multiplicado por (-1) é um número positivo entre 0 e 0,5. Este número é o coeficiente de Poisson ν (carta grega) de So.

[TOC]

Fórmula do coeficiente de Poisson

Para calcular o coeficiente de Poisson, é necessário determinar a deformação da unidade longitudinal e transversal.

Deformação da unidade longitudinal ε_eu É o trecho dividido entre o comprimento original:

ε_eu = (L ' - L) / L

Da mesma forma, deformação unitária transversal ε_T É o estreitamento radial dividido entre o diâmetro original:

ε_T = (D ' - D) / D

Portanto, o coeficiente de Poisson é calculado pela seguinte fórmula:

ν = - ε_T / ε_eu 

Relação com o módulo de elasticidade e o módulo de rigidez

O coeficiente de Poisson ν está relacionado ao módulo E de elasticidade (ou módulo jovem) e com o módulo de rigidez G, Pela fórmula a seguir:

Pode atendê -lo: óptica geométrica: que estudos, leis, aplicações, exercícios

ν = e /(2g) - 1

Valor do coeficiente de Poisson para materiais

Figura 2. O aço inoxidável tem coeficiente de Poisson entre 0,30 e 0,31. Fonte: Pixabay.

Exemplos de cálculo

Exemplo 1

Uma barra de um determinado material plástico tem um comprimento de 150 mm e seção circular de 20 mm de diâmetro. Quando uma força de compressão de 612,25 kg-f é submetida a uma força de compressão, um encurtamento de 14 mm é observado e simultaneamente um aumento de 0,85 mm no diâmetro da barra.

Calcular:

a) deformação unitária longitudinal.

b) Deformação unitária transversal.

c) o coeficiente de Poisson desse material.

d) o módulo de elasticidade do jovem correspondente ao material.

e) o módulo de rigidez para esse plástico.

Solução para

Lembre -se de que a deformação da unidade longitudinal εl é o trecho dividido pelo comprimento original:

εl = (l ' - l) / l

εl = (-14 mm) / 150 mm = -0,0933

Observe que a deformação unitária longitudinal é adimensional e, neste caso, deu negativo porque houve uma diminuição em sua dimensão longitudinal.

Solução b

Da mesma forma, a deformação transversal unitária εt é estreitada radial, dividida pelo diâmetro original:

εt = (D ' - D) / D

εt = (+0,85 mm) / 20 mm = 0,0425

A deformação unitária transversal tem sido positiva porque houve um aumento no diâmetro da barra.

Solução c

Para o cálculo do coeficiente de Poisson, devemos lembrar que ele é definido como o negativo do quociente entre deformação transversal e deformação longitudinal:

ν = - εt / εl 

ν = - 0,0425 / (-0,0933) = 0,4554

Deve -se lembrar que o coeficiente de Poisson é um número positivo de dimensão e, para a maioria dos materiais, está entre 0 e 0,5.

Pode atendê -lo: Darcy Law

Solução d

O módulo de elasticidade de Young, indicado pela letra E, é a constante de proporcionalidade na lei de Hooke. Através de E, o esforço normal σL está relacionado à deformação unitária εl, como segue:

σl = e εl 

O esforço normal é definido como o quociente entre a força normal (neste caso, paralela ao eixo da barra) e a seção transversal:

σl = f / a = f / (π / 4 * d^2)

Neste exercício, a força F é 612,25 kg-f, que será feita a Newtons que é a unidade de força:

F = 612,25 kg-f = 612,25 * 9,8 n = 6000 n = 6 kN

Por sua vez, a seção transversal A é:

A = (π/4 * d^2) = (3.1416/4) * (20 * 10^-3 m)^2 = 3.1416 * 10^-4 m^2

Finalmente, o esforço normal aplicado ao bar é:

σl = f / a = 6000 n / 3.1416 * 10^-4 m^2 = 19.098.593 PA = 19.098 MPA

Para calcular o módulo de elasticidade do jovem, limpamos e da lei de Hooke σl = e εl:

E = σl / εl = 19.098.593 PA / 0,0933 = 204,7 MPA

Solução e

O módulo de rigidez R está relacionado ao módulo EG de Young e ao coeficiente de Poisson ν por esta fórmula:

E / (2 g) = 1 + ν 

De lá você pode limpar G:

G = e / (2 (1 + ν)) = 204,7 MPa / (2 (1 + 0,4554)) = 70,33 MPa

Exemplo 2

Você tem um cabo de 4 mm e 1 m de comprimento. Sabendo que o módulo jovem de cobre é de 110000 MPa e que seu coeficiente de Poisson é de 0,34, estima o alongamento e o estreitamento do diâmetro que o fio sofre quando um peso de 100 kg-f.

Solução

Em primeiro lugar, é necessário calcular o esforço normal de tração que o peso exerce no fio, seguindo esta fórmula:

Pode atendê -lo: vetores no espaço: como representar graficamente, aplicações, exercícios

σl = f / a = f / (π / 4 * d^2)

A força F é 980 n e a seção transversal é:

A = (π/4 * d^2) = (3.1416/4) * (4 * 10^-3 m)^2 = 1.2566 * 10^-5 m^2

Então o esforço de tração é:

σl = 980 n / 1.2566 * 10^-5 m^2 = 77.986.000 Pa

Cálculo da deformação do fio unitário

O módulo de elasticidade de Young, indicado pela letra E, é a constante de proporcionalidade na lei de Hooke que relaciona o esforço normal σl à deformação unitária εl:

σl = e εl 

A partir daí, a deformação unitária longitudinal do fio de cobre pode ser limpa:

εl = σl / e = 77.986 MPa / 110000 MPa = 7,09 * 10^-4

Cálculo da deformação unitária transversal

Por outro lado, para conhecer a deformação unitária transversal, o coeficiente de Poisson é aplicado:

ν = - εt / εl 

Finalmente, você tem que deformação unitária transversal é: 

εt = -ν εl = -0,34 * 7,09 * 10 ^-4 = -2,41 * 10 ^-4

Cálculo absoluto de alongamento do cabo

Finalmente, para conhecer o alongamento absoluto do cabo, o seguinte relacionamento deve ser aplicado:

Δl = εl * l = 7,09 * 10^-4 * 1 m = 7,09 * 10^-4 m = 0,709 mm

Isto é, com esse peso, o cabo quase se estendeu 0,709 milímetros.

Cálculo da diminuição do diâmetro

Para obter encolhimento absoluto de diâmetro, usamos a seguinte fórmula:

ΔD = εt * d = -2,41 * 10 ^-4 * 4 mm = -9,64 * 10 ^-4 mm = -0.000964 milímetros.

Esse estreitamento em diâmetro é tão pequeno que é difícil apreciar a olho nu, até sua medição requer um instrumento de alta precisão.

Referências

1. Cerveja f ... mecânica de material. 5 ª. Edição. 2010. Mc Graw Hill. 1-130.
2. Hibbeler R. Mecânica de Materiais. Oitava edição. Prentice Hall. 2011. 3-60.
3. Gere J. Mecânica de Materiais. Oitava edição. Cengage Learning. 4-220.
4. Giancoli, d. 2006. Física: Princípios com aplicações. 6ª ed. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. Notas de física geral. Unam. 87-98.