Estágios de ciclo de carnot, aplicações, exemplos, exercícios

Ele Ciclo de Carnot É a sequência de processos termodinâmicos que ocorrem em um motor Carnot, um dispositivo ideal que consiste apenas em processos reversíveis; isto é, aqueles que, tendo ocorrido, podem retornar ao estado inicial.

Esse tipo de motor é considerado ideal, pois não possui a dissipação, atrito ou viscosidade que surgem em máquinas reais, transformando a energia térmica em trabalho utilizável, embora a conversão não seja realizada 100%.

figura 1. Uma locomotiva a vapor. Fonte: Pixabay

Um motor é construído com base em uma substância capaz de fazer trabalho, como gás, gasolina ou vapor. Esta substância está sujeita a várias mudanças de temperatura e, por sua vez, experimenta variações em sua pressão e volume. Dessa forma, é possível mover um pistão dentro de um cilindro.

[TOC]

Qual é o ciclo de carnot?

O ciclo Carnot ocorre dentro de um sistema chamado Carnot ou C Motor, que é um gás ideal travado em um cilindro e fornecido com um pistão, que está em contato com duas fontes a diferentes temperaturas t₁ e T₂ como o mostrado na figura a seguir à esquerda.

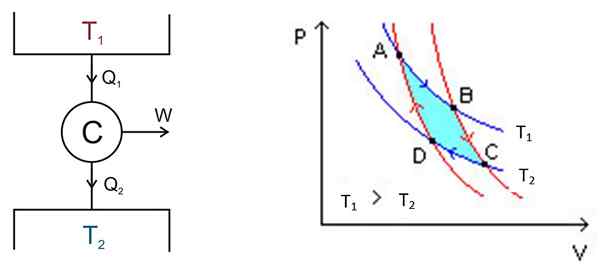Figura 2. À esquerda, um esquema da máquina C Arnot, à direita, o diagrama PV. Fonte da figura esquerda: Keta - Trabalho próprio, CC por 2.5, https: // Commons.Wikimedia.org/w/índice.Php?Curid = 681753, figura direita Wikimedia Commons.

Existem os seguintes processos em modo aproximado:

1. Uma certa quantidade de calor é fornecida ao dispositivo_Entrada = Q₁ Do tanque térmico a alta temperatura t₁.
2. O motor Carnot C realiza um trabalho W graças a este calor fornecido.
3. Uma parte do calor usado: o lixo q_saída, É transferido para o tanque térmico que está em uma temperatura mais baixa t₂.

Estágios do ciclo de carnot

A análise é feita por um diagrama P -V (pressão -volume), como mostrado na Figura 2 (figura direita). O objetivo do motor pode ser manter o depósito térmico 2 frio, extraindo calor dele. Nesse caso, é um Máquina de refrigerante. Se, pelo contrário, você deseja dar calor ao depósito térmico 1, então é um bomba de calor.

O diagrama P -V mostra mudanças de pressão - temperatura do motor sob duas condições:

- Mantendo a temperatura constante (processo isotérmico).

- Sem transferência de calor (isolamento térmico).

Os dois processos isotérmicos precisam ser conectados, o que é alcançado por meio de isolamento térmico.

Ponto de partida

Você pode começar em qualquer momento do ciclo, no qual o gás tem certa pressão, volume e condições de temperatura. O gás sofre uma série de processos e pode retornar às condições de partida para iniciar outro ciclo, e sempre a energia interna final é a mesma que a inicial. Como a energia é preservada:

Trabalho realizado por c = calor de entrada - calor de partida

Δw = q_Entrada - Q_saída

A área incluída neste ciclo ou loop, em turquesa na figura, é igual precisamente ao trabalho realizado pelo motor Carnot.

Os pontos A, B, C e D estão marcados na Figura 2. Começará no momento para seguir a flecha azul.

Primeira etapa: expansão isotérmica

A temperatura entre os pontos A e B é t₁. O sistema absorve o calor do depósito térmico 1 e sofre uma expansão isotérmica. Então o volume aumenta e a pressão diminui.

No entanto, a temperatura permanece em t₁, Desde quando o gás se expande. Portanto, sua energia interna permanece constante.

Pode servir a você: Graff Van Gerador: Partes, como funciona, aplicativos

Segundo estágio: expansão adiabática

No ponto B, o sistema começa uma nova expansão na qual o sistema não ganha ou perde calor. Isso é conseguido colocando -o em isolamento calórico, conforme indicado antes. Portanto, é uma expansão adiabática que continua a apontar C após a seta vermelha. O volume aumenta e a pressão diminui até atingir seu menor valor.

Terceiro estágio: compressão isotérmica

Comece no ponto C e termine em D. O isolamento é removido e o sistema entra em contato com o depósito térmico 2, cuja temperatura t₂ É menor. O sistema produz resíduos de calor para o tanque térmico, a pressão começa a aumentar e o volume para diminuir.

Quarto estágio: compressão adiabática

Alcançado para o ponto D, o sistema remonta ao isolamento térmico, a pressão aumenta e o volume diminui até atingir as condições originais do ponto a. Então o ciclo é repetido novamente.

Teorema de Carnot

O teorema de Carnot foi postulado pela primeira vez no início do século 19 pelo físico francês Sadi Carnot. No ano de 1824, Carnot, que fazia parte do exército francês, publicou um livro no qual ele propôs a resposta para a seguinte pergunta: em que condições uma máquina térmica tem eficiência máxima? Carnot então estabeleceu o seguinte:

Nenhum motor térmico em execução entre dois depósitos térmicos é mais eficiente que o motor Carnot.

O rendimento η de um motor térmico é dado pela razão entre o trabalho realizado e o calor absorvido Q:

performance = trabalho feito/calor absorvido

Dessa forma, o desempenho de qualquer motor térmico I é: η = w/q. Enquanto o desempenho de um motor Carnot R é η '= w/q', no caso de ambos os motores, eles são capazes de executar o mesmo trabalho.

O teorema de Carnot afirma que η nunca é maior que η '. Caso contrário, se enquadra em contradição com a segunda lei da termodinâmica, segundo a qual é impossível ir a um processo em que o resultado é que o calor de um corpo de temperatura mais baixa é impossível de ir para outra temperatura mais alta sem receber ajuda externa. Portanto:

η _< η^'

Demonstração do teorema de Carnot

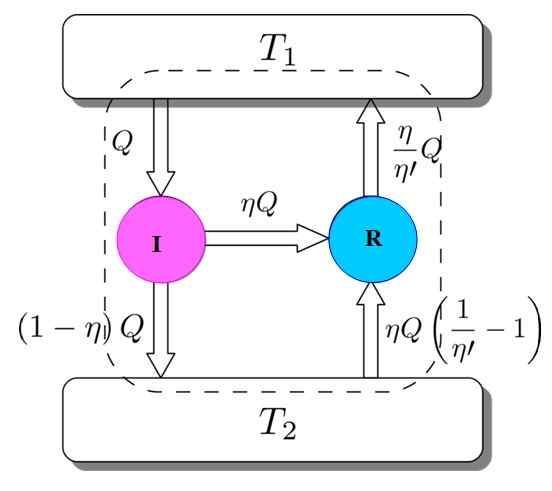
Para mostrar que é assim, considere o motor Carnot atuando como uma máquina de geladeira acionada por um mecanismo I. Isso é possível, pois o motor Carnot funciona por processos reversíveis, conforme especificado no início.

Figura 3. Demonstração do teorema de Carnot. Fonte: Netheril96 [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenças/BY-SA/3.0)]

Você tem os dois: eu e R trabalhando com os mesmos depósitos térmicos e será assumido que η _> η^'. Se, ao longo do caminho, uma contradição for alcançada com a segunda lei da termodinâmica, o teorema de Carnot é demonstrado pela redução do absurdo.

Figura 3 ajuda a seguir o processo. O mecanismo I pega uma quantidade de calor Q, que se divide dessa maneira: funcionando em r equivalente a w = ηq e o restante é o calor transferido (1 -η) q para o tanque térmico t₂.

Como a energia é preservada, tudo é cumprido:

E_Entrada = Q = trabalho w + calor atribuído a t₂ = ηq + (1 -η) q = e_saída

Agora a máquina de geladeira Carnot R leva o tanque térmico 2 Uma quantidade de calor dada por:

Pode servir a você: IMANTATION: O que consiste, método e exemplos

(η / η ') (1 -η') q =

A energia também deve ser mantida neste caso:

E_Entrada = ηq + (η / η ') (1 -η') q = (η / η ') q = q' = e_saída

O resultado é a transferência para o tanque térmico t₂ de uma quantidade de calor dada por (η / η ') q = q'.

Se η for maior que η 'significa que o depósito térmico de maior temperatura chegou mais calor do que eu tomava originalmente. Como nenhum agente externo, como outra fonte térmica, participou, a única maneira de acontecer é que o depósito térmico mais frio produz o calor.

Isso discorda da segunda lei da termodinâmica. Conclui -se então que não é possível que η^' Seja menor que η, portanto o motor I não pode ter mais desempenho do que a máquina Carnot R.

Corolário do teorema e limitações

O Corolário do Teorema de Carnot afirma que duas máquinas Carnot têm a mesma eficiência se ambas operarem com os mesmos depósitos térmicos.

Isso significa que a substância não importa, o desempenho é independente e não pode ser aumentado alterando -a.

A conclusão da análise anterior é que o ciclo Carnot é o topo do processo termodinâmico idealmente atingível. Na prática, existem muitos fatores que diminuem a eficiência, por exemplo, o fato de que o isolamento nunca é perfeito e em estágios adiabáticos, na verdade, há troca calórica com o exterior.

No caso de um carro, o bloco do motor é aquecido. Por outro lado, a mistura de gás e ar não se comporta exatamente como um gás ideal, que é o ponto de partida do ciclo Carnot. Isso mencionar apenas alguns fatores que causarão uma redução drástica de desempenho.

Exemplos

Um pistão dentro de um cilindro

Se o sistema for um pistão travado em um cilindro como na Figura 4, o pistão aumenta durante a expansão isotérmica, como pode ser visto no primeiro esquema da extrema esquerda e também aumenta durante a expansão adiabática.

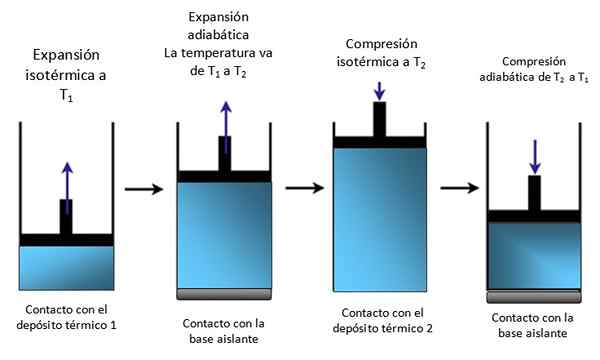Figura 4. Movimento de um pistão dentro de um cilindro. Fonte: Self feito.

Em seguida, isotermicamente comprimido, dando calor e continua a compactar adiabaticamente. O resultado é um movimento em que o pistão se eleva e desce dentro do cilindro e pode ser transmitido a outras partes de um determinado dispositivo, como um motor de carro, por exemplo, que produz um par ou uma máquina fumegante.

Vários processos reversíveis

Além da expansão e compressão de um gás ideal dentro de um cilindro, existem outros processos reversíveis ideais com os quais um ciclo de carnot pode ser configurado, por exemplo:

- Movimentos de ida e volta na ausência de atrito.

- Uma mola ideal que é compactada e descomprimida e que nunca se deforma.

- Circuitos elétricos nos quais não há resistência que dissipa energia.

- Ciclos de magnetização e desmagnetização em que não há perdas.

- Carregando e baixando uma bateria.

Uma usina nuclear

Embora seja um sistema muito complexo, uma primeira abordagem do que é necessário para produzir energia no reator nuclear é o que se segue:

- Uma fonte térmica, consistindo de um material que se desintegra radioativamente como o urânio.

Pode atendê -lo: modelo atômico atual

- A pia ou depósito térmico frio que seria a atmosfera.

- A "máquina Carnot" que usa um fluido, quase sempre.

Quando o ciclo é realizado, a eletricidade é obtida como um trabalho líquido. Quando transformado em vapor de alta temperatura, a água é alcançada em uma turbina, onde a energia é transformada em movimento ou energia cinética.

A turbina, por sua vez, ativa um gerador elétrico que transforma a energia de seu movimento em eletricidade. Além do material de fistor como o urânio, é claro que os combustíveis fósseis podem ser usados ​​como fonte de calor.

Exercícios resolvidos

-Exemplo 1: Eficiência de uma máquina térmica

A eficiência de uma máquina térmica é definida como a razão entre o trabalho de saída e o trabalho de entrada e, portanto, é uma quantidade adimensional:

Eficiência máxima = (q_Entrada - Q _saída) /Q_Entrada

Denotando a eficiência máxima como e_máx, É possível demonstrar sua dependência de temperatura, que é a variável mais fácil de medir, como:

e_máx = 1 - (T₂/T₁)

Onde t₂ É a temperatura da pia e t₁ É a temperatura da fonte térmica. Como o último é maior, a eficiência sempre acaba sendo menor que 1.

Suponha que uma máquina térmica seja capaz de trabalhar das seguintes maneiras: a) entre 200 k e 400 K, b) entre 600 K e 400 K. Qual é a eficiência em cada caso?

Solução

a) No primeiro caso, a eficiência é:

e_Max1 = 1 - (200/400) = 0.cinquenta

b) Para o segundo modo, a eficiência será:

e_Max2 = 1- (400/600) = 0.33

Embora a diferença de temperatura seja a mesma entre os dois modos, a eficiência não é. E ainda mais notável é que o modo mais eficiente opera em temperatura mais baixa.

-Exemplo 2: calor absorvido e calor cedido

Uma máquina térmica de 22 % produz 1530 j de trabalho. Encontre: a) A quantidade de calor absorvida do depósito térmico 1, b) a quantidade de calor descartado para o tanque térmico 2.

a) Nesse caso, a definição de eficiência é usada, pois o trabalho realizado, não das temperaturas dos depósitos térmicos está disponível. 22% de eficiência significa que e _Máx = 0.22, portanto:

Eficiência máxima = trabalho /q_Entrada

A quantidade de calor absorvida é precisamente Q_Entrada, Então, limpeza que você tem:

Q_Entrada = Trabalho/eficiência = 1530 J/0.22 = 6954.5 J

b) A quantidade de calor atribuída ao tanque mais frio é de δW = q_Entrada - Q_saída

Q_saída = Q_Entrada - ΔW = 6954.5 -1530 J = 5424.5 J.

Outra maneira é de e_máx = 1 - (T₂/T₁). Como as temperaturas não são conhecidas, mas elas estão relacionadas ao calor, a eficiência também pode ser expressa como:

e_máx = 1 - (Q_Bastão/Q_absorvido)

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill. 654-657
2. Energia nuclear. Operação de uma usina nuclear. Recuperado de: energia-nuclear.líquido
3. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning. 618-622.
4. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. MacGraw Hill. 414-416.
5. Walker, J.2008. Física. 4ª ed.Addison Wesley. 610-630