Propriedades das células unitárias, constante e tipos vermelhos

O Célula unitária É um espaço ou região imaginária que representa a expressão mínima de um todo; Que no caso da química, o todo seria um cristal composto por átomos, íons ou moléculas, que são ordenados seguindo um padrão estrutural.

Na vida cotidiana, você pode encontrar exemplos que incorporem este conceito. Para isso, é necessário prestar atenção a objetos ou superfícies que exibem uma certa ordem repetitiva de seus elementos. Alguns mosaicos, resultação, artesanato.

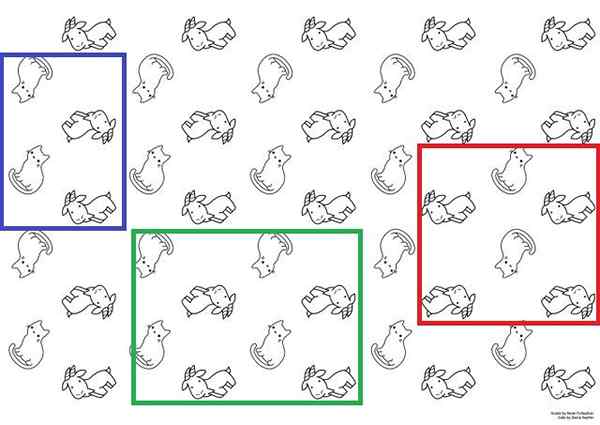Células unitárias em papel de gato e cabra. Fonte: Hanna Petruschat (WMDE) [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenças/BY-SA/4.0)].

Para ilustrá -lo com mais clareza, você tem a imagem superior que pode ser usada como um papel de tapeçaria. Nele, gatos e cabras aparecem com dois sentidos alternativos; Gatos são pés ou cabeça, e as cabras olhando para cima ou para baixo.

Esses gatos e cabras estabelecem uma sequência estrutural repetitiva. Para construir todo o artigo, seria suficiente reproduzir a célula unitária pela superfície um número suficiente de vezes, por meio de movimentos de tradução.

As células unitárias possíveis são representadas com as caixas azuis, verdes e vermelhas. Qualquer um desses três pode ser usado para obter o papel; Porém, é necessário movê -los imaginários ao longo da superfície para descobrir se eles reproduzem a mesma sequência observada na imagem.

Começando com a caixa vermelha, seria apreciado que, se três colunas (de gatos e cabras) fossem movidas para a esquerda, duas cabras não apareceriam mais em sua parte inferior, mas apenas uma. Portanto, levaria a outra sequência e não pode ser considerado como uma célula unitária.

Embora se eles imaginassem as duas caixas, azul e verde, a mesma sequência de papel seria obtida. Ambos são células unitárias; No entanto, a caixa azul obedece mais à definição, pois é menor que a caixa verde.

[TOC]

Propriedades da célula unitária

Sua própria definição, além do exemplo recém -explicado, esclarece várias de suas propriedades:

-Se eles se moverem no espaço, independentemente da direção, o sólido ou vidro completo será obtido. Isso ocorre porque, como mencionado com gatos e cabras, eles reproduzem a sequência estrutural; que é igual à distribuição espacial de unidades repetitivas.

-Eles devem ser o mais pequeno possível (ou ocupar pouco volume) em comparação com outras possíveis opções de células.

Pode atendê -lo: ácido metilmalônico: estrutura, propriedades, síntese, usos

-Eles são, comuns, simétricos. Da mesma forma, sua simetria é literalmente refletida nos cristais do composto; Se a célula unitária de um sal for cúbica, seus cristais serão cúbicos. No entanto, existem estruturas cristalinas descritas com células unitárias com geometrias distorcidas.

-Eles contêm as unidades repetitivas, que podem ser substituídas por pontos, que na curva três -dimensionalmente o que é conhecido como retículo. No exemplo anterior, gatos e cabras representam os pontos reticulares, vistos de um plano mais alto; isto é, duas dimensões.

Número de unidades repetitivas

As unidades repetitivas ou pontos reticulares das células unitárias mantêm a mesma proporção das partículas sólidas.

Se o número de gatos e cabras forem contados dentro da caixa azul, haverá dois gatos e cabras. O mesmo vale para a caixa verde, e com a caixa vermelha (mesmo que já se saiba que não é uma célula unitária).

Suponha, por exemplo, que gatos e cabras sejam átomos G e C, respectivamente (uma soldagem de animais estranha). Como a proporção entre G e C é 2: 2 ou 1: 1 na caixa azul, pode -se esperar, sem erros, que o sólido terá a fórmula GC (ou CG).

Quando o sólido possui estruturas mais ou menos compactas, como em sais, metais, óxidos, sulfetos e ligas, nas células unitárias, não há unidades repetitivas inteiras; Ou seja, existem partes ou partes deles, que somam uma ou duas unidades.

Este não é o caso do GC. Se a caixa azul "começaria" a gatos e cabras em dois (1/2g e 1/2c) ou quatro partes (1/4g e 1/4c). Nas próximas seções, verá que nessas células unitárias os pontos reticulares são convenientemente divididos desta e de outras maneiras.

Quais constantes de rede definem uma célula unitária?

As células unitárias do exemplo do GC são bilimensionais; No entanto, isso não se aplica nos modelos reais que consideram as três dimensões. Assim, as caixas ou paralelogramas são transformados em paralelepípedos. Agora, o termo "célula" assume maior sentido.

As dimensões dessas células ou paralelepípedes dependem de quanto tempo são seus respectivos lados e ângulos.

Na imagem inferior, você tem o canto traseiro inferior do paralelepípedo, composto pelos lados para, b e c, e os ângulos α, β e γ.

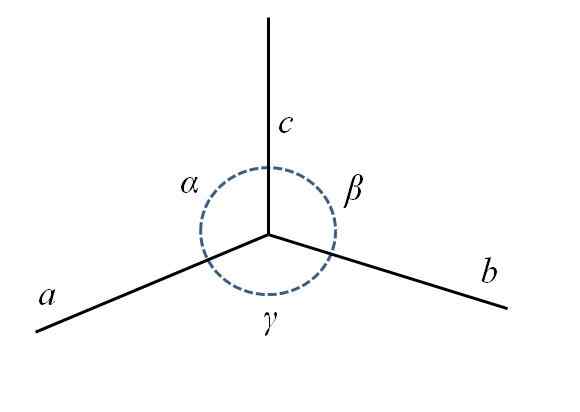Parâmetros de uma célula unitária. Fonte: Gabriel Bolívar.

Como você pode ver, para é um pouco mais longo do que b e c. No centro, você tem um círculo com uma linha pontilhada para indicar os ângulos α, β e γ, entre AC, Cb e BA, respectivamente. Para cada célula unitária, esses parâmetros têm valores constantes e definem sua simetria e o restante do vidro.

Pode atendê -lo: peróxido de cálcio (CaO2): propriedades, riscos e usos

Aplicando alguma imaginação novamente, os parâmetros da imagem definiriam uma célula semelhante a um cubo esticado em sua borda para. Assim, as células unitárias surgem com diferentes comprimentos e ângulos de suas bordas, que também podem ser classificados em vários tipos.

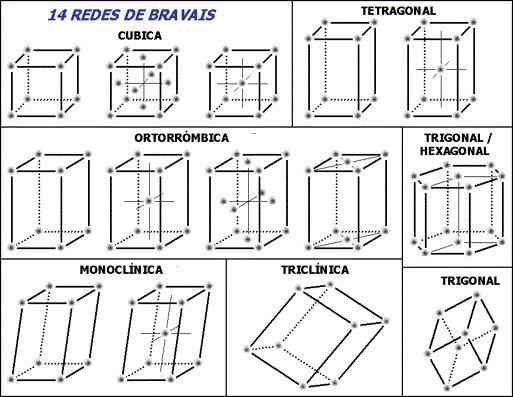
Pessoal

As 14 redes Bravais e os sete sistemas cristalinos básicos. Fonte: O uploader original era raiva da Wikipedia portuguesa. [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/]]

Nota para iniciar as linhas pontilhadas dentro das células da unidade: elas indicam o ângulo traseiro inferior, conforme explicado. A seguinte pergunta pode ser feita, onde estão os pontos reticulares ou unidades repetitivas? Embora eles dêem a impressão errada de que as células estão vazias, em seus vértices a resposta está.

Essas células são geradas ou escolhendo de tal maneira que, em seus vértices, as unidades repetitivas estão localizadas (pontos cinzentos da imagem). Dependendo dos valores dos parâmetros estabelecidos na seção anterior, constante para cada célula unitária, sete sistemas cristalinos são derivados.

Cada sistema cristalino tem sua própria célula unitária; O segundo define o primeiro. Na imagem superior, existem sete caixas, correspondendo aos sete sistemas cristalinos; ou um pouco mais de resumo, redes cristalinas. Assim, por exemplo, uma célula unitária cúbica corresponde a um dos sistemas cristalinos que define uma rede cristalina cúbica.

De acordo com a imagem, os sistemas ou redes cristalinas são:

-Cúbico

-Tetragonal

-Ortorrombica

-Hexagonal

-Monoclínico

-Triclínico

-Trigonal

E dentro desses sistemas cristalinos, outros que compõem os quatorze redes de Bravais; que entre todas as redes cristalinas, elas são as mais básicas.

Cúbico

Em um cubo, todos os seus lados e ângulos são os mesmos. Portanto, o seguinte é cumprido nesta célula unitária:

para = b = c

α = β = γ = 90º

Existem três células unitárias cúbicas: simples ou primitivas, centradas no corpo (BCC) e centradas em faces (FCC). As diferenças estão em como os pontos (átomos, íons ou moléculas) e no número deles são distribuídos.

Qual dessas células é a mais compacta? Que cujo volume está mais ocupado por pontos: o cúbico centrado nos rostos. Observe que, se substituirmos os pontos pelos gatos e cabras do começo, eles não estariam confinados a uma única célula; Eles pertencem e seriam compartilhados por vários. Novamente, seria partes de g ou c.

Pode servir você: hidrocolóide

Número de unidades

Se gatos ou cabras estivessem nos vértices, eles seriam compartilhados por 8 células unitárias; Isto é, cada célula teria 1/8 de g ou c. Juntos ou imagine 8 cubos, em duas colunas de duas linhas cada, para visualizá -lo.

Se gatos ou cabras estivessem no rosto, eles seriam compartilhados apenas por 2 células unitárias. Para ver, basta reunir dois cubos.

Por outro lado, se o gato ou cabra estivesse no centro do cubo, eles pertencem apenas a uma única célula unitária; O mesmo acontece com as caixas da imagem principal, quando o conceito foi abordado.

Disse então o exposto acima, dentro de uma célula cúbica simples a Unidade ou ponto reticular, pois possui 8 vértices (1/8 x 8 = 1). Para a célula cúbica centrada no corpo que você tem: 8 vértices, que são iguais a um átomo, e um ponto ou unidade no centro; Portanto, existe dois unidades.

E para a célula cúbica centrada nos rostos que você tem: 8 vértices (1) e seis faces, onde na qual metade de cada ponto ou unidade é compartilhada (1/2 x 6 = 3); Portanto, tem quatro unidades.

Tetragonal

Comentários semelhantes podem ser feitos em relação à célula unitária para o sistema tetragonal. Seus parâmetros estruturais são os seguintes:

para = b ≠ c

α = β = γ = 90º

Ortorrombica

Os parâmetros para a célula ortorrombic são:

para ≠ b ≠ c

α = β = γ = 90º

Monoclínico

Os parâmetros da célula monoclínica são:

para ≠ b ≠ c

α = γ = 90º; β ≠ 90º

Triclínico

Os parâmetros para a célula triclínica são:

para ≠ b ≠ c

α ≠ β ≠ γ ≠ 90º

Hexagonal

Os parâmetros para a célula hexagonal são:

para = b ≠ c

α = β = 90º; γ ≠ 120º

Na verdade, a célula constitui a terceira parte de um prisma hexagonal.

Trigonal

E, finalmente, os parâmetros para a célula trigonal são:

para = b = c

α = β = γ ≠ 90º

Referências

1. Whitten, Davis, Peck e Stanley. (2008). Química. (8ª ed.). Cengage Learning P 474-477.
2. Shiver & Atkins. (2008). Química Inorgânica. (Quarta edição). Mc Graw Hill.
3. Wikipedia. (2019). Célula primitiva. Recuperado de: em.Wikipedia.org
4. Bryan Stephanie. (2019). Célula unitária: parâmetros de latice e estruturas cúbicas. Estudar. Recuperado de: estudo.com
5. Centro de Recursos Acadêmicos. (s.F.). Estruturas cristalinas. [PDF]. Instituto de Tecnologia de Illinois. Recuperado de: web.IIT.Edu
6. Belford Robert. (7 de fevereiro de 2019). Crystal Latices e Células Unitárias. Química Librettexts. Recuperado de: química.Librettexts.org