Conceitos de análise de malha, métodos, exemplos

Ele Análise de malha É uma técnica usada para resolver circuitos elétricos planos. Este procedimento também pode aparecer na literatura com os nomes de métodos do correntes de circuito o Método de Correntes de malha (ou loop).

A fundação deste e de outros métodos de análise de circuito elétrico está nas leis de Kirchhoff e da Lei de Ohm. As leis de Kirchhoff, por sua vez, são expressões de dois princípios muito importantes de conservação em física para sistemas isolados: tanto a carga elétrica quanto a energia são preservadas.

figura 1. Os circuitos fazem parte de inúmeros dispositivos. Fonte: Pixabay.

Por um lado, a carga elétrica está relacionada à corrente, que está movendo carga, enquanto em um circuito a energia está ligada à tensão, que é o agente responsável por fazer o trabalho necessário para manter a carga em movimento.

Essas leis, aplicadas a um circuito plano, geram um conjunto de equações simultâneas que devem ser resolvidas para obter valores de corrente ou tensão.

O sistema de equações pode ser resolvido com técnicas analíticas já conhecidas, como Regra de Cramer, que requer o cálculo dos determinantes para obter a solução do sistema.

Dependendo do número de equações, elas são resolvidas usando uma calculadora científica ou um software matemático. Na rede, também existem muitas opções disponíveis.

[TOC]

Termos importantes

Antes de explicar como funciona, começaremos definindo estes Termos:

Filial: Seção contendo um elemento do circuito.

Nó: apontar que conecta dois ou mais ramos.

Fita: É qualquer parte fechada de um circuito, que começa e termina no mesmo nó.

Malha: loop que não contém nenhum outro vínculo dentro (malha essencial).

Métodos

A análise de meheal é um método geral que serve para resolver circuitos cujos elementos são conectados em série, paralelamente ou misturados, ou seja, quando o tipo de conexão não é claramente distinguido. O circuito deve ser plano, ou pelo menos deve ser possível retribuir como tal.

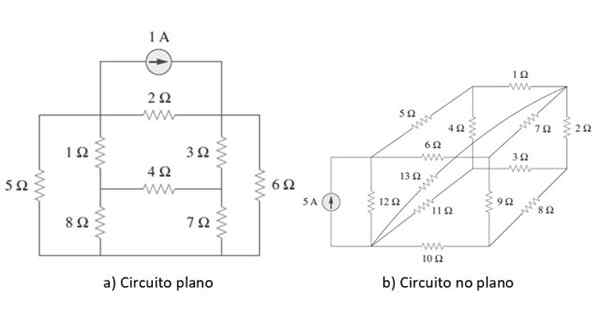Figura 2. Circuitos planos e não -flat. Fonte: Alexander, C. 2006. Fundações de circuito elétrico. 3º. Edição. Mc Graw Hill.

Um exemplo de cada tipo de circuito é mostrado na figura acima. Uma vez que o ponto for esclarecido, para começar, aplicaremos o método a um circuito simples como exemplo na próxima seção, mas antes de revisar brevemente as leis de Ohm e Kirchhoff.

Lei de Ohm: Sean V A tensão, R A resistência e Yo A corrente do elemento resistivo ôhmico, no qual a tensão e a corrente são diretamente proporcionais, sendo a resistência a constante da proporcionalidade:

Pode atendê -lo: API Gravity: escala e classificação do petróleo bruto

V = i.R

Lei de Kirchhoff de tensão (LKV): Em qualquer trajetória fechada viajada em uma direção, a soma algébrica das tensões é zero. Isso inclui tensões devido a fontes, resistores, indutores ou capacitores: ∑ e = ∑ r_Yo. Yo

Kirchhoff do atual (LKC): Em qualquer nó, a soma algébrica das correntes é zero, levando em consideração que as correntes que entram recebem um sinal e para o qual outro sai. Dessa forma: ∑ i = 0.

Com o método de correntes de malha, não é necessário.

- Etapas para aplicar a análise de malha

Começaremos a explicar o método para um circuito de 2 malhas. O procedimento pode ser estendido posteriormente para circuitos maiores.

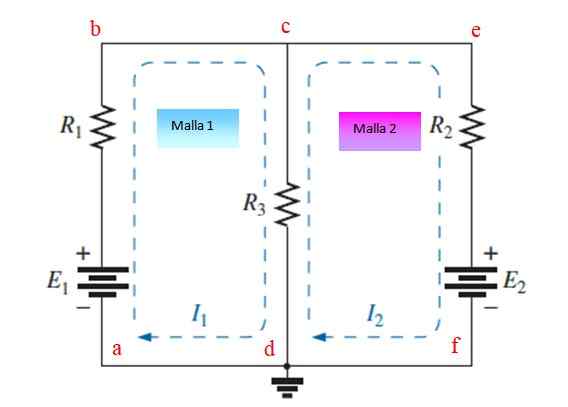Figura 3. Circuito com resistências e fontes dispostas em duas malhas. Fonte: f. Zapata.

Passo 1

Atribuir e desenhar correntes independentes a cada malha, neste exemplo elas são Yo₁ e Yo₂. Eles podem ser desenhados em um cronograma ou também anti -marário.

Passo 2

Aplique a lei de tensões de Kirchhoff (LTK) e a lei de Ohm a cada malha. As quedas em potencial recebem um sinal (-) enquanto os aumentos são atribuídos signo (+).

Malha abcda

A partir do ponto A e, seguindo o significado da corrente, encontramos um aumento no potencial na bateria E1 (+), depois uma queda em r₁ (-) e depois outra queda em r₃ (-).

Simultaneamente, a resistência r₃ Também é atravessado pela corrente i₂, Mas na direção oposta, portanto, representa uma ascensão (+). A primeira equação é assim:

E₁-R₁.Yo₁ -R₃.Yo₁ + R₃.Yo₂ = 0

Conseguir imediatamente os termos de promoção:

- (R₁+R₃) Yo₁ +R₃Yo₂ = -E₁  (Equação 1)

Malha Cefdc 

Começando do ponto e e seguir o significado da corrente é uma queda potencial em R₂ (-), outra queda E₂, Desde que a corrente entra no pólo da bateria e finalmente se enquadra R₃ (-), ao mesmo tempo a corrente Yo₁ Atravessa R₃ Na direção oposta (+).

A segunda equação, com os sinais indicados, permanece dessa maneira:

- R₂ Yo₂ - E₂ -R₃ Yo₂ +R₃ Yo₁= 0

R₃Yo₁ - (R₂ +R₃₎ Yo₂ = E₂  (Equação 2)

Observe que existem duas equações com as duas incógnitas e₁ e eu₂.

etapa 3

Então o sistema de equações assim formado é resolvido.

Exercícios resolvidos

Para começar, é importante levar em consideração o seguinte:

-Os laços ou correntes de malha podem receber uma direção arbitrária.

-Para cada malha essencial - ou "janela" - que o circuito deve receber uma corrente.

Pode atendê -lo: processo isocórico

-As correntes de malha são chamadas com letras maiúsculas para distingui -las das correntes que circulam em ramos, embora em alguns casos a corrente que circula através de um ramo possa ser igual à da malha.

- Exemplo 1

Encontre as correntes que circulam por cada resistência no circuito na Figura 3, se os elementos tiverem os seguintes valores:

R₁ = 20 Ω; R₂ = 30 Ω; R₃ = 10 Ω; E₁ = 12 V; E₂ = 18 v

Solução

Em primeiro lugar, é necessário atribuir as correntes de malha e₁ e eu₂ e pegue o sistema de equações deduzido na seção anterior e substitua os valores fornecidos na declaração:

- (R₁+R₃) Yo₁ +R₃Yo₂ = -E₁  (Equação 1)

R₃Yo₁ - (R₂ +R₃₎ Yo₂ = E₂     (Equação 2)

-

-(20+30) Yo₁ + 10i₂ = -12

10i₁ - (30 +10) I₂ = 18      

--

-cinquentaYo₁ + 10i₂ = -12

10i₁ - 40 i₂ = 18      

Como é um sistema de 2 x 2 equações, ele pode ser facilmente resolvido pela redução, multiplicando por 5 a segunda equação para eliminar desconhecida Yo₁:

-cinquentaYo₁ + 10 i₂ = -12

50i₁ - 200 i₂ = 90

-     

-190 i₂= 78

Yo₂ = - 78/180 a = - 0.41 a

A corrente é imediatamente limpa Yo₁ de qualquer uma das equações originais:

Yo₁ = (18 + 40 i₂) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 a

O sinal negativo na corrente Yo₂ significa que a corrente na malha 2 circula contrária ao desenho.

As correntes em cada resistência são as seguintes:

Para resistência R₁ A corrente circula Yo₁ = 0.16 a No sentido desenhado, por resistência R₂ A corrente circula Yo₂ = 0.41 a ao contrário do desenhado, e por resistência R₃ circula Yo₃ = 0.16- (-0.41) a = 0.57 a para baixo.

Solução do sistema pelo método de Cramer

De uma maneira matriz, o sistema pode ser resolvido da seguinte maneira:

Etapa 1: Calcule δ

 Importante: Quando δ = 0, o sistema não tem solução, é um sistema incompatível.

Etapa 2: Calcule δ₁

A primeira coluna é substituída pelos termos independentes do sistema de equações, mantendo a ordem em que o sistema foi originalmente levantado:

Etapa 3: Calcule eu₁

Yo₁ = Δ₁/Δ = 300/1900 = 0.16 a

Etapa 4: Calcule δ₂

 Etapa 5: Calcule eu₂

Yo₂ = Δ₂/Δ = -780/1900 = -0.41 a

- Exemplo 2

Determine a corrente e as tensões através de cada resistência no circuito a seguir, por meio do método das correntes de malha:

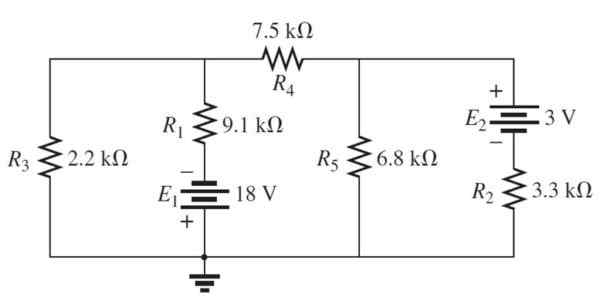Figura 4. 3 circuito de malha. Fonte: Boylestad, r. 2011. Introdução à análise do circuito.2º. Edição. Pearson.

Solução

As três correntes de malha são desenhadas, como mostrado na figura a seguir, em sentidos arbitrários. Agora as malhas estão correndo de qualquer lugar:

Pode servir a você: IMANTATION: O que consiste, método e exemplos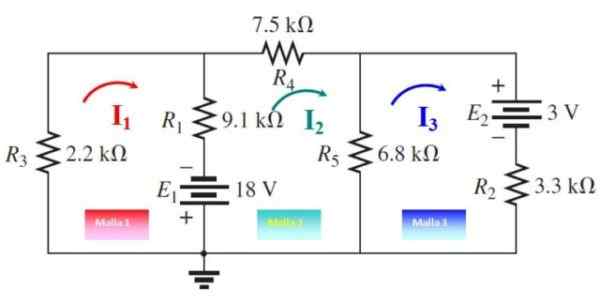 Figura 5. Correntes de malha para o exercício 2. Fonte: f. Zapata, modificado de Boylestad.

Malha 1

-9100.Yo₁+18-2200.Yo₁+9100.Yo₂= 0

-11300 i₁ + 9100.Yo₂ = -18

Malha 2       

-(7500 +6800 +9100) .Yo₂ + 9100.Yo₁+6800.Yo₃-18 = 0

9100.Yo₁ - 23400.Yo₂ + 6800.Yo₃ = 18

Malha 3  

-(6800 + 3300) I₃ + 6800.Yo₂ - 3 = 0

6800.Yo₂ - 10100.Yo₃ = 3

Sistema de equações

-11300 i₁ + 9100.Yo₂ + 0.Yo₃= -18

9100.Yo₁ - 23400.Yo₂ + 6800.Yo₃ = 18

0.Yo₁ + 6800.Yo₂ - 10100.Yo₃ = 3

Embora os números sejam grandes, é rapidamente resolvido com a ajuda de uma calculadora científica. Lembre -se de que as equações devem ser ordenadas e adicionar zeros nos lugares onde o desconhecido não aparece, como aparece aqui.

As correntes de malha são:

Yo₁ = 0.0012 a; Yo₂ = -0.00048 a; Yo₃ = -0.00062 a

As correntes Yo₂ e Yo₃ Eles circulam na direção oposta na figura, uma vez que acabaram sendo negativos.

Tabela de correntes e tensões em cada resistência

Resistência (ω)	Atual (AMPS)	Tensão = i.R (volts)
9100	Yo1 -Yo2 = 0.0012-(-0.00048) = 0.00168	quinze.3
3300	0.00062	2.05
2200	0.0012	2.64
7500	0.00048	3.60
6800	Yo2 -Yo3= -0.00048-(-0.00062) = 0.00014	0.95

Solução de regras de Cramer

Como são grandes números, é conveniente usar a notação científica para trabalhar com eles diretamente.

Cálculo de i₁

Setas coloridas no determinante 3 x 3 indicam como encontrar valores numéricos, multiplicando os valores indicados. Vamos começar obtendo os do primeiro suporte no determinante δ:

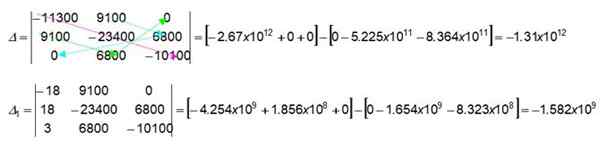
(-11300) x (-23400) x (-10100) = -2.67 x 10¹²

9100 x 0 x 0 = 0

9100 x 6800 x 0 = 0

Obtemos imediatamente o segundo suporte nesse mesmo determinante, que funciona da esquerda para a direita (para este suporte, as setas coloridas não foram desenhadas na figura). Convidamos o leitor a verificar:

0 x (-23400) x 0 = 0

9100 x 9100 x (-10100) = -8.364 x 10^onze

6800 x 6800 x (-11300) = -5.225 x 10^onze

Da mesma maneira, o leitor também pode verificar os valores para o determinante Δ₁.

Importante: Entre os dois colchetes, sempre há um sinal negativo.

Finalmente a corrente é obtida Yo₁ através Yo₁ = Δ₁ / Δ

Yo₁ = -1.582 x 10⁹/-1.31 x 10¹² = 0.0012 a                                   

Cálculo de i₂

O procedimento pode ser repetido para calcular Yo₂, Nesse caso, para calcular o determinante δ₂ A segunda coluna do determinante Δ é substituída pela coluna dos termos independentes e seu valor é encontrado, de acordo com o procedimento explicado.

No entanto, como é pesado por causa de grandes números, especialmente se não houver calculadora científica, o mais simples é substituir o valor de Yo₁ Já calculado, na seguinte equação e claro:

-11300 i₁ + 9100.Yo₂ + 0.Yo₃= -18 → 9100 i₂= -18 + 11300 i₁ → i₂ = -0.00048 a

I3 Cálculo

Uma vez com os valores de Yo₁ e Yo₂ Na mão, o Yo₃ É encontrado diretamente por substituição.

Referências

1. Alexander, c. 2006. Fundações de circuito elétrico. 3º. Edição. Mc Graw Hill.
2. Boylestad, r. 2011. Introdução à análise do circuito.2º. Edição. Pearson.
3. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 5. Interação elétrica. Editado por Douglas Figueroa (USB).
4. Garcia, l. 2014. Eletromagnetismo. 2º. Edição. Universidade Industrial de Santander.
5. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 2.