Aceleração da gravidade o que é, como é medido e exercícios

O Aceleração da gravidade o A aceleração gravitacional é definida como a intensidade do campo gravitacional da terra. Isto é, a força que isso exerce em qualquer objeto, por unidade de massa.

É indicado com a letra já familiar G e seu valor aproximado nas proximidades da superfície da Terra é 9.8 m/s². Esse valor pode experimentar pequenas variações com latitude geográfica e também com a altura em relação ao nível do mar.

Astronauta no espaço Paseo na superfície da terra. Fonte: Pixabay

A aceleração da gravidade, além de ter a magnitude mencionada, tem direção e significado. De fato, é direcionado verticalmente para o centro da terra.

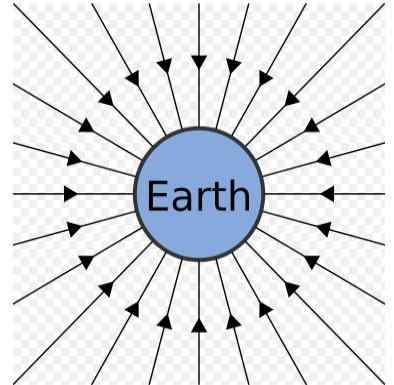Campo gravitacional da terra. Fonte: Fonte: SJLEGG [Domínio Público]

O campo gravitacional da Terra pode ser representado como um conjunto de linhas radiais que apontam para o centro, como pode ser visto na figura anterior.

[TOC]

Qual é a aceleração da gravidade?

O valor da aceleração da gravidade na terra ou em qualquer outro planeta é equivalente à intensidade do campo gravitacional que produz, que não depende dos objetos que estão ao seu redor, mas apenas de sua própria massa e seu raio.

Freqüentemente, a aceleração da gravidade é frequentemente definida como a aceleração experimentada por qualquer objeto em queda livre nas proximidades da superfície da Terra.

Na prática, isso é o que quase sempre acontece, como veremos nas seções a seguir, nas quais a lei universal de gravitação universal de Newton será usada.

Dizem que Newton descobriu esta famosa lei enquanto meditava na queda dos corpos sob uma árvore. Ao sentir o golpe da maçã em sua cabeça, ele imediatamente soube que a força que faz a maçã cair é a mesma que faz com que a lua orbite ao redor da terra.

A lei de gravitação universal

Certa ou não a lenda da Apple, Newton percebeu que a magnitude da força de atração gravitacional entre dois objetos, por exemplo, entre a terra e a lua, ou a terra e a maçã, teve que depender das massas delas:

Onde m₁ Pode ser a massa da terra e m_2, A massa da lua ou maçã. Uma massa maior, uma maior atração existe entre os corpos. Mas a mais distância, menos força, pois isso deve ser inversamente proporcional ao quadrado de distância r que os separa:

Pode servir a você: choques elásticos: em uma dimensão, casos especiais, exercícios

Isso é verdade, independentemente de quão grande ou pequeno são as massas em questão. Ao combinar esses fatos, a força da gravidade permaneceria dessa maneira:

É necessária uma constante de proporcionalidade para ter esta lei empírica pronta. Newton calculou a constante G, de modo que a fórmula descreve com toda a precisão os movimentos dos corpos celestes na escala do sistema solar e além:

Onde g = 6.67 x 10^-onze N.m²/kg²

Características da força gravitacional

A força gravitacional é sempre atraente; isto é, os dois corpos aos quais afeta são atraídos um pelo outro. O oposto não é possível, uma vez que as órbitas dos corpos celestes são fechados ou abertos (cometas, por exemplo) e uma força de repulsão nunca pode produzir uma órbita fechada. Então as massas sempre atraem, o que quer que aconteça.

Uma abordagem bastante boa para a forma real da terra (M₁) E a lua ou maçã (M₂) é assumir que eles têm uma forma esférica. A figura a seguir é uma representação desse fenômeno.

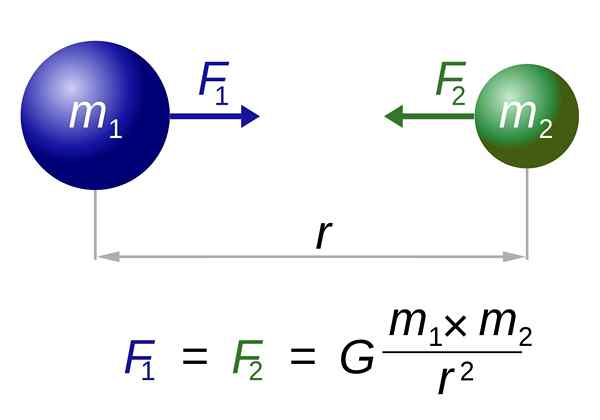Lei de Gravitação Universal de Newton. Fonte: I, Dennis Nilsson [CC por 3.0 (https: // CreativeCommons.Org/licenças/por/3.0)]

Aqui estão ambos a força exercida M₁ Sobre m₂, Como aquele que exerce m₂ Sobre m₁, ambos de igual magnitude e direcionados ao longo da linha que se junta aos centros. Eles não são cancelados, pois são aplicados a diferentes objetos.

Em todas as seções a seguir, supõe -se que os objetos sejam homogêneos e esféricos, portanto, seu centro de gravidade coincide com seu centro geométrico. Toda massa concentrada pode ser assumida apenas lá.

Como a gravidade é medida em diferentes planetas?

A gravidade pode ser medida com um liêméter, um aparelho que serve para fazer a seriedade medida em pesquisas gravimétricas geofísicas. Atualmente, eles são muito mais sofisticados que os originais, mas no começo foram baseados no pêndulo.

O pêndulo consiste em uma corda fina, clara e inestável de comprimento l. Um de seus finais é fixado em um suporte e o outro pendura uma massa m.

Quando o sistema está em equilíbrio, a massa está pendurada na vertical, mas quando é separada dele, começa a oscilar a execução de um movimento de balanço. A gravidade é responsável por isso. Para tudo o que se segue, é válido assumir que a gravidade é a única força que age no pêndulo.

Pode servir a você: balão aerostático: história, características, partes, como funciona

O período de balanço do pêndulo para pequenas oscilações, é dado pela seguinte equação:

A força t não depende da massa, mas do comprimento do L e do valor de g. Square, os dois membros da equação são:

O relacionamento entre T² e eu É linear: uma linha do formulário y = a.x, onde o valor de para, A inclinação da linha é precisamente (4π²/g).

Experimentar para determinar o valor de g

Materiais

- 1 esferito de metal.

- Corda de vários comprimentos diferentes, pelo menos 5.

- Fita métrica.

- Transportador.

- Cronômetro.

- Um suporte para definir o pêndulo.

- Milimetering Paper ou Computer Program com planilha.

Procedimento

1. Selecione uma das cordas e monte o pêndulo. Meça o comprimento da corda + o raio da esfera. Este será o comprimento l.
2. Remova o pêndulo da posição de equilíbrio a cerca de 5 graus (identifique -o com o transportador) e deixe -o oscilado.
3. Inicie simultaneamente o cronômetro e meça o tempo de 10 oscilações. Anote o resultado.
4. Repita o procedimento anterior para os outros comprimentos.
5. Encontre o tempo que leva o pêndulo para executar uma oscilação (dividindo cada um dos resultados anteriores por 10).
6. Quadrado cada valor obtido, obtendo t²
7. No artigo milímetro, represente cada valor de T² No eixo vertical, contra o respectivo valor de L no eixo horizontal. Seja consistente com as unidades e não se esqueça de levar em consideração o erro de apreciação dos instrumentos utilizados: fita métrica e stopwatch.
8. Desenhe a melhor linha que se encaixa nos pontos gráficos.
9. Encontre a ladeira m desta linha usando dois pontos que pertencem a ela (não necessariamente pontos experimentais). Adicione o erro experimental.
10. As etapas acima podem ser realizadas com uma planilha e a opção de construir e ajustar uma linha reta.
11. Do valor da inclinação para limpar o valor de g Com sua respectiva incerteza experimental.

Valor padrão de g Na terra, na lua e em Marte

O valor padrão da gravidade na Terra é: 9.81 m/s², aos 45 de latitude do norte e no nível do mar. Como a Terra não é uma esfera perfeita, os valores de g Eles variam um pouco, sendo maiores nos pólos e menores do Equador.

Aqueles que desejam conhecer o valor em sua localidade podem encontrá -lo atualizado no site do Instituto de Metroções da Alemanha PTB (Physikalisch-Technische BundesAnstalt), na seção Sistema de informação por gravidade (GIZ).

Pode servir a você: Diretor Vector: Equação direta, exercícios resolvidos

A gravidade na lua

O campo gravitacional da lua foi determinado pela análise dos sinais de rádio do espaço sondas que orbitam o satélite. Seu valor na superfície lunar é 1.62 m/s²

A gravidade em Marte

O valor de g_P Para um planeta, depende de sua massa m e seu raio da seguinte forma:

Portanto:

Para o planeta Marte, os seguintes dados estão disponíveis:

M = 6.4185 x 10²³ kg

R = 3390 km

G = 6.67 x 10^-onze N.m²/kg²

Com esses dados, sabemos que a gravidade de Marte é 3.71 m/s². Naturalmente, a mesma equação pode ser aplicada aos dados da lua ou qualquer outro planeta e, assim, estimar o valor de sua gravidade.

Exercício resolvido: a maçã que cai

Suponha que tanto a terra quanto a maçã tenham uma forma esférica. A massa da terra é m = 5,98 x 10²⁴ kg e seu raio é r = 6,37 x 10⁶  m. A massa da maçã é m = 0.10 kg. Suponha que não haja outra força, exceto a da gravidade. Da lei de gravitação universal de Newton:

a) a força gravitacional exercida na maçã.

b) A aceleração experimentada pela Apple ao liberá -la de uma certa altura, de acordo com a segunda lei de Newton.

Solução

a) A maçã (suposta esférica, assim como a terra) tem um raio muito pequeno em comparação com o raio terrestre e está imerso em seu campo gravitacional. A figura a seguir não é evidentemente, mas há um esquema do campo gravitacional g, e a força F Exerorado pela Terra na Apple:

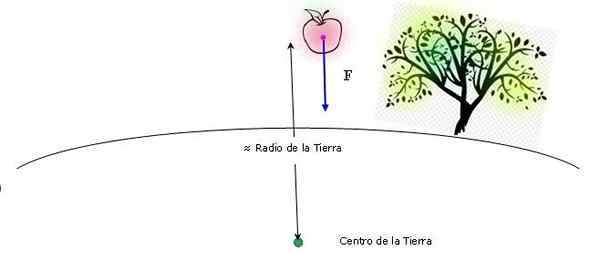Esquema que mostra a queda da maçã nas proximidades da terra. Tanto o tamanho da maçã quanto a altura da queda são desprezíveis. Fonte: Self feito.

Ao aplicar a lei de gravitação universal de Newton, a distância entre os centros pode ser considerada aproximadamente o mesmo valor que o raio da terra (a altura da qual a maçã cai também é insignificante em comparação com o raio terrestre). Portanto:

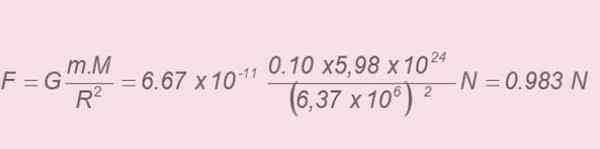
b) De acordo com a segunda lei de Newton, a magnitude da força exercida na maçã é:

F = ma = mg

Cujo valor é 0.983 n, de acordo com o cálculo anterior. Equalizando os dois valores e depois a limpeza da magnitude da aceleração é obtida:

mg = 0.983 n

G = 0.983 N/0.10 kg = 9.83 m/s²

Esta é uma abordagem muito boa para o valor padrão da gravidade.

Referências

1. Giancoli, d. (2006). Física: Princípios com aplicações. Sexta edição. Prentice Hall. 118-122.
2. Hewitt, Paul. (2012). Ciência física conceitual. QUINTA EDIÇÃO. Pearson. 91 - 94.
3. Rex, a. (2011). Fundamentos da Física. Pearson. 213-221.