Definição de aceleração centrípeta, fórmulas, cálculo, exercícios

O aceleração centrípeta para_c, Também chamado de radial ou normal, é a aceleração que carrega um objeto móvel ao descrever uma trajetória circular. Sua magnitude é v²/r, onde r É o raio do círculo, é direcionado para o centro e é responsável pelo celular permanecer em sua rota.

As dimensões da aceleração centrípeta são de comprimento por unidade de tempo. No sistema internacional, eles são M/s². Se, por algum motivo.

Os objetos giratórios têm aceleração centrípeta, que é direcionada para o centro da trajetória. Fonte: Pixabay

É o que acontece com um carro que tenta dar uma curva em uma pista plana e geada, na qual o atrito entre o piso e as rodas é insuficiente para que o carro tome a curva. Portanto, a única possibilidade que você deixou é se mover em uma linha reta e é por isso que você sai da curva.

[TOC]

Movimentos circulares

Quando um objeto se move em círculo, o tempo todo a aceleração centrípeta é radialmente direcionada para o centro da circunferência, a direção perpendicular à trajetória seguida.

Como a velocidade é sempre tangente à trajetória, a velocidade e a aceleração centrípeta acabam sendo perpendiculares. Portanto, velocidade e aceleração nem sempre têm a mesma direção.

Nessas circunstâncias, o celular tem a possibilidade de descrever a circunferência com velocidade constante ou variável. O primeiro caso é conhecido como movimento circular uniforme ou mCU por sua sigla, o segundo caso será um movimento circular variável.

Pode atendê -lo: qual é a limpeza de emissão? (Com exemplos)

Nos dois casos, a aceleração centrípeta é responsável por manter a circulação móvel, ocupando que a velocidade varia apenas na direção e na direção.

No entanto, para ter um movimento circular variável, seria necessário outro componente de aceleração na mesma direção da velocidade, o que é responsável por aumentar ou diminuir a velocidade. Este componente de aceleração é conhecido como Aceleração tangencial.

O movimento circular variável e o movimento curvilíneo em geral têm ambos os componentes da aceleração, porque o movimento curvilíneo pode imaginar como a rota através de inúmeros arcos de circunferência que compõem a trajetória curva.

A força centrípeta

Agora, uma força é responsável por fornecer aceleração. Para um satélite que orbita a terra, é a força da gravidade. E como a gravidade sempre age perpendicular à trajetória, ela não altera a velocidade do satélite.

Nesse caso, a gravidade atua como um força centrípeta, que não é uma aula especial ou além da força, mas que no caso do satélite é radialmente direcionada para o centro da terra.

Em outros tipos de movimento circular, por exemplo, um carro que toma uma curva, o papel da força centrípeta é interpretado pela força estática que força o celular a girar.

Fórmulas para aceleração centrípeta

A aceleração centrípeta é calculada pela expressão:

AC = v²/r

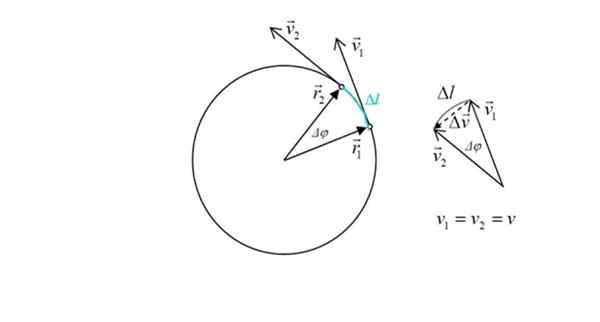Diagrama para calcular a aceleração centrípeta em um celular com MCU. Fonte: Fonte: Ilevanat [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenças/BY-SA/3.0)]

Esta expressão será deduzida abaixo. Por definição, a aceleração é a variação da velocidade no tempo:

Pode servir a você: fontes de luz: tipos e dispositivos que emitem luz

O diagrama superior mostra na figura esquerda, dois pontos pelos quais um celular passa que se move em um círculo de rádio r em um sentido anti -horium. Observe que a magnitude da velocidade é a mesma nos dois casos, mas não na direção ou significado.

O celular usa tempo δt Na turnê, que é pequena, já que os pontos estão muito próximos.

A figura também mostra dois vetores de posição r₁ e r₂, cujo módulo é o mesmo: o rádio r da circunferência. O ângulo entre os dois pontos é Δφ. Em verde o arco Tour pelo celular, indicado como ΔL.

Na figura à direita, é visto que a magnitude de δv, A mudança na velocidade é aproximadamente proporcional a ΔL, uma vez que o ângulo Δφ é pequeno. Mas a mudança de velocidade está relacionada com precisão à aceleração. O triângulo é avisado, pela soma dos vetores que:

v₁ + Δv = v₂ → δv = v₂ - v₁

Δv É interessante, pois é proporcional à aceleração centrípeta. A partir da figura, é avisado de que ser pequeno ângulo Δφ, vetor δv É em essência perpendicular ambos v₁ Como a v₂ e aponta para o centro da circunferência.

Embora os vetores se destacem em negrito, para os efeitos da natureza geométrica que se segue, trabalhamos com os módulos ou magnitudes desses vetores, independentemente da notação vetorial.

Outra coisa: você precisa usar a definição de ângulo central, que é:

Δφ= Δl/r

Agora ambos os números são comparados, que são proporcionais, pois o ângulo δφ é comum:

Pode atendê -lo: o que é luz polarizada?

 

Dividindo entre Δt:

 Como a definição de velocidade é v = Δl/ Δt. Mas δV/ Δt É precisamente a magnitude da aceleração centrípeta, que é o que é procurado. Dessa maneira, a expressão descrita no início é alcançada:

para_c= v²/r

Exercício resolvido

Uma partícula se move em um círculo de 2.Rádio de 70 m. Em um determinado momento, sua aceleração é 1.05 m/s² Em uma direção que faz um ângulo de 32.0º com a Diretoria de Movimento. Calcule sua velocidade:

a) Naquela época

b) 2.00 segundos depois, assumindo uma aceleração tangencial constante.

Responder

É um movimento circular variado, uma vez que a declaração indica que a aceleração tem um determinado ângulo com a direção do movimento que não é ou 0º (não poderia ser um movimento circular) ou 90º (seria um movimento circular uniforme).

Portanto, os dois componentes - radial e tangencial - coexistem. Será denotado como_c já_t e parecer desenhado na figura seguinte. O vetor verde é o vetor de aceleração líquido ou simplesmente aceleração para.

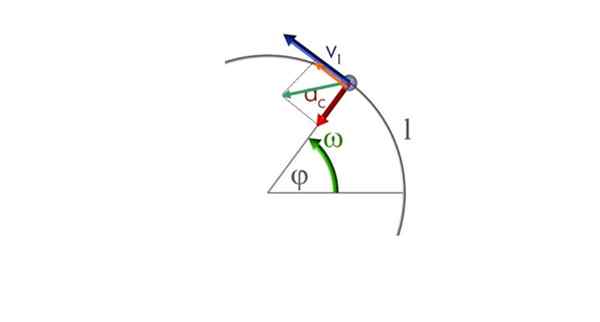Uma partícula se move em uma trajetória circular em um sentido anti -historário e movimento circular variado. Fonte: Commons.Wikimedia.org

a) Cálculo de componentes de aceleração

para_c = a.cos θ = 1.05 m/s² . cos 32.0º = 0.89 m/s² (em vermelho)

para_t = a.sin θ = 1.05 m/s² . Sen 32.0º = 0.57 m/s² (em laranja)

Cálculo da velocidade móvel

Desde um_c = v²/r, então:
b) 2 segundos depois a velocidade v será aumentado graças ao componente tangencial da aceleração

v = v_qualquer +para_t. T = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s

Referências

1. Giancoli, d. Física. 2006. Princípios com aplicações. Sexta edição. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Ciência física conceitual. QUINTA EDIÇÃO.Pearson.106 - 108.