Absorvância o que é, exemplos e exercícios resolvidos

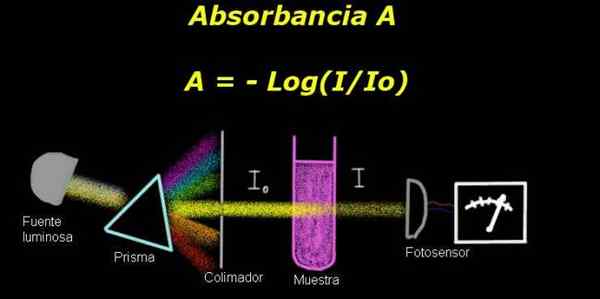
O absorvância É o logaritmo com um sinal negativo do quociente entre a intensidade da luz emergente e a intensidade do incidente da luz em uma amostra de solução translúcida que foi iluminada com luz monocromática. Este quociente é o transmitância.

O processo físico da passagem da luz através de uma amostra é chamado transmissão luminosa, E a absorvância é uma medida disso. Portanto, a absorvância se torna o menor logaritmo de transmitância e é um fato importante para determinar a concentração de uma amostra que geralmente é dissolvida em um solvente como água, álcool ou qualquer outro.

figura 1. Esquema do processo de absorvância. Preparado por f. Zapata

Para medir a absorvância, é necessário um dispositivo Eletro-fotômetro, com o qual uma corrente é medida proporcional ao incidente de intensidade luminosa em sua superfície.

Ao calcular a transmitância, o sinal da intensidade correspondente ao solvente sozinho é geralmente medido e esse resultado é registrado como Io.

Então a amostra dissolvida no solvente com as mesmas condições de iluminação é colocada. A medida medida pelo eletro-fotômetro é denotada como Yo, que permite que você calcule a transmitância T De acordo com a seguinte fórmula:

T = i / iqualquer

É uma quantidade desencadeada. O Absorvância a Isso é expresso como:

A = - log (t) = - log (i / iqualquer)

[TOC]

Absorvância molar e absorção

As moléculas que compõem um produto químico são capazes de absorver a luz, e uma medida disso é com precisão. É o resultado da interação entre fótons e elétrons moleculares.

Portanto, é uma magnitude que dependerá da densidade ou concentração das moléculas que compõem a amostra e também do caminho óptico ou distância percorrida pela luz. 

Você pode atendê -lo: terceira lei de Newton: pedidos, experimentos e exercícios

Dados experimentais indicam que a absorvora PARA é linearmente proporcional à concentração C e distância d A luz viajou. Portanto, para calculá -lo com base nesses parâmetros, a seguinte fórmula pode ser estabelecida:

A = ε⋅c⋅d

Na fórmula anterior, ε É uma constante de proporcionalidade conhecida pelo nome de Absorção molar.

A absorção molar depende do tipo de substância e comprimento de onda com o qual a absorvância é medida. O Absorção molar Também é sensível à temperatura da amostra e ao pH do mesmo.

Lei de Beer-Lambert

Essa relação entre absorvância, absorção, concentração e distância da espessura do caminho que a luz segue dentro da amostra é conhecida como Lei de Beer-Lambert.

Figura 2. Lei de Cerveja - Lambert. Fonte: f. Zapata,

Abaixo, existem alguns exemplos de como usá -lo.

Exemplos

Exemplo 1

Durante um experimento, uma amostra com uma luz vermelha de uma luz de laser de hélio-neon, cujo comprimento de onda é 633 nm. Um eletro-fotômetro mede 30 mV quando a luz do laser afeta diretamente e 10 mV quando passa por uma amostra. 

Nesse caso, a transmitância é:

T = i / io = 10 mV / 30 mV = ⅓.

E a absorvância é:

A = - log (⅓) = log (3) = 0,48 

Exemplo 2

Se a mesma substância for colocada em recipiente que tem metade do espesso.

Deve -se considerar que, se a espessura diminuir para a metade, a absorvância proporcional à espessura óptica diminui pela metade, ou seja, a = 0,28. A transmitância de toneladas será dada pelo seguinte relacionamento:

Pode servir a você: Tiro vertical: fórmulas, equações, exemplos

T = 10-a = 10^(-0.28) = 0,53

O eletro-fotômetro marcará 0,53*30 mV = 15,74 mV.

Exercícios resolvidos

Exercício 1

É desejado determinar a absorção molar de um certo composto patenteado que está em solução. Para isso, a solução com luz de uma lâmpada de sódio de 589 nm é iluminada. A amostra será colocada com 1,50 cm de espessura.

É baseado em uma solução de concentração 4,00 × 10^-4 moles por litro e a transmitância é medida, resultando em 0,06. Determinar com esses dados a absorção molar da amostra.

Solução 

Em primeiro lugar, a absorvância é determinada, o que é definido como o menor logaritmo baseado em dez de transmitância:

A = - log (t)

A = - log (0,06) = 1,22

Em seguida, é usada a lei de Lambert-Beer que estabelece uma relação entre absorvância, absorção molar, concentração e comprimento óptico:

A = ε⋅c⋅d

Limpando a absorção molar O seguinte relacionamento é obtido:

ε = a/(c⋅d)

Substituindo os valores fornecidos:

ε = 1,22/(4,00 × 10^-4 m⋅1,5 cm) = 2030 (m⋅cm)^-1

O resultado anterior foi arredondado para três dígitos significativos.

Exercício 2

Para melhorar a precisão e determinar o erro da medida da absorção molar da amostra no Exercício 1, a amostra é sucessivamente diluída na metade da concentração e a transmitância é medida em cada caso.

A partir de CO = 4 × 10^-4 m com transmitância t = 0,06 A seguinte sequência de dados para transmitância e absorvância calculada a partir da transmitância é obtida:

CO/1-> 0,06-> 1,22

CO/2-> 0,25-> 0,60

CO/4-> 0,50-> 0,30

CO/8-> 0,71-> 0,15

CO/16-> 0,83-> 0,08

CO/32-> 0,93-> 0,03

CO/64-> 0,95-> 0,02

CO/128-> 0,98-> 0,01

CO/256-> 0,99-> 0,00

Com esses dados, faça:

Pode servir a você: ondas estacionárias: fórmulas, características, tipos, exemplos

a) Um gráfico de absorvância baseado na concentração.

b) um ajuste linear dos dados e encontre a inclinação.

c) A partir da inclinação obtida, calcule a absorção molar.

Solução 

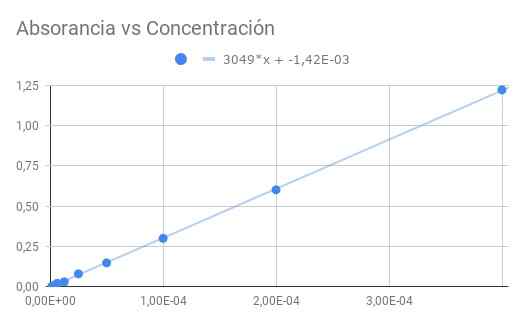Figura 3. Absorvância versus concentração. Fonte: f. Zapata.

A inclinação obtida é o produto da absorganividade molar pela distância óptica; portanto, dividindo a inclinação por comprimento 1,5 cm, obtemos absorção molar

ε = 3049/1,50 = 2033 (m⋅cm)^-1

Exercício 3

Com os dados do Exercício 2: 

a) Calcule a absorvor de absorção para cada dados. 

b) determinar um valor médio para a absorção molar, seu desvio padrão e o erro estatístico associado à média.

Solução 

A absorção molar é calculada para cada uma das concentrações testadas. Lembre -se de que as condições de iluminação e a distância óptica permanecem fixas.

Os resultados da absorção molar são:

2033, 2007, 2007, 1983, 2158, 1681, 2376, 1.872, 1862 em unidades de 1/(m*cm).

A partir desses resultados, podemos assumir o valor médio:

= 1998 (m*cm)^-1

Com um desvio padrão de: 184 (m*cm)^-1

O erro médio é o desvio padrão dividido pela raiz quadrada do número de dados, ou seja::

Δ = 184/9^0,5 = 60 (m*cm)^-1

Finalmente, conclui -se que a substância patenteada tem uma absorção molar na frequência 589 nm produzida por uma lâmpada de sódio de:

= (2000 ± 60) (m*cm)^-1

Referências

1. Atkins, p. 1999. Química Física. Edições Omega. 460-462.
2. A guia. Transmitância e absorvância. Recuperado de: química.LaGuia2000.com
3. Toxicologia Ambiental. Transmitância, absorvância e lei de Lambert. Recuperado de: repositório.Innovationumh.é
4. Física de aventura. Absorvância e transmitância. Recuperado de: rpfisica.Blogspot.com
5. Sistofotometria. Recuperado de: química.Librettexts.org
6. Toxicologia Ambiental. Transmitância, absorvância e lei de Lambert. Recuperado de: repositório.Innovationumh.é
7. Wikipedia. Absorvância. Recuperado de: Wikipedia.com
8. Wikipedia. Espectrofotometria. Recuperado de: Wikipedia.com