Volume

Explicamos qual é o volume, suas fórmulas, unidades, como calculá -lo e dar vários exemplos

Qual é o volume?

Ele volume de um corpo é o valor numérico que mede a quantidade de espaço ocupada por ele. A alta, largura e profundidade determinam o volume, quanto maior, maior o espaço ocupado.

O conceito de volume é de grande importância, pois o mundo é tridimensional e todos os objetos têm largura, altura e profundidade, portanto, eles têm volume. As pessoas usam frequentemente, por exemplo, estimando se os móveis que desejam comprar, se encaixam no quarto ou se entram em um determinado tamanho do vestido.

Em certas áreas de ciência e engenharia, como ao trabalhar com fluidos, sejam líquidos ou gases, o volume ocupado adquire grande importância: ao encher recipientes e bombear fluidos, como água ou no projeto de um navio para um navio para garantir que Você não afunda. Tudo isso torna essencial determinar para muitos processos.

Existem fórmulas para calcular o volume de corpos geométricos em formas regulares, como prismas, esferas, cilindros e cones, por exemplo, dependendo de algumas de suas dimensões. E também existem maneiras de descobrir o volume de objetos irregulares, como será descrito um pouco mais tarde.

Fórmulas de volume em figuras geométricas

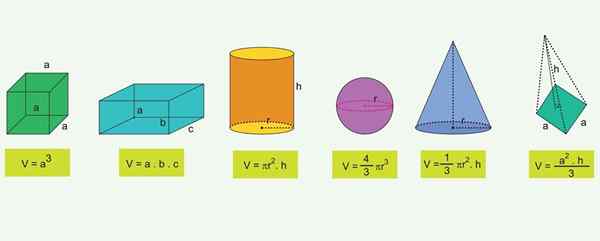Lista dos números geométricos mais comuns e a fórmula de seus volumes

Para os objetos geométricos mais conhecidos, existem fórmulas que permitem calcular seu volume:

• Cubo

V = ℓ³ 

Onde v representa o volume e ℓ é a borda (lateral) do cubo.

• Paralelepípedo

Um paralelepípedo é uma caixa retangular com largura "a", longa e "h" altura. Seu volume é dado pelo produto de suas três dimensões:

V = a ∙ ℓ ∙ h

• Esfera

O volume da esfera depende de seu raio r:

Pode atendê -lo: nicolás copernico

• Cilindro circular reto

O volume do cilindro circular reto é o produto entre a área de sua base e sua altura "h". Como a base é um álbum de rádio "R", cuja área é a = π · r², O volume permanece:

V = πr²∙ h

• Bichano

O volume do cone é um terço do produto entre a área da base circular A e a altura H. Como um = πr², então:

• Pirâmide

Para uma pirâmide cuja área base é A e tem uma altura "H", o volume é dado por:

Se a pirâmide tiver uma base quadrada ao lado "A", como na figura, a área base da base é para² E o volume da pirâmide é:

V = (1/3) ⋅A²⋅H

• Prisma

O volume do prisma é o produto entre a área da base A e a altura "H":

V = a ∙ h

Unidades de volume

No sistema internacional de unidades, a unidade de volume é o metro cúbico ou M³, enquanto no sistema anglo -saxon é o pé cúbico ou ft³ (de Pés, que em inglês significa "pé").

Existem muitas outras unidades, de acordo com o tamanho do espaço ocupado. Por exemplo, quilômetros cúbicos de km³ Para volumes maiores ou milímetros cúbicos mm³ Para pequenos volumes. Também existem unidades de uso local.

Também é necessário mencionar as unidades de capacidade, intimamente relacionadas às do volume, que são preferencialmente usadas para líquidos. A unidade de capacidade central é o litro, abreviado L, que é equivalente a um DM³ (Decímetro cúbico).

Outras unidades que valem a pena mencionar são o galão, a polegada cúbica, a xícara e a gota, a última usada para dosar os medicamentos.

Pode atendê -lo: método comparativo

Como o volume é medido?

O volume de um corpo, como qualquer outra medida, é realizado em comparação com um padrão adequado, neste caso uma unidade de volume.

A unidade de volume é definida como o cubo cuja borda mede 1 unidade. Esta unidade pode ser um medidor, centímetro, pé, polegada ou qualquer outro. Então, o volume do objeto corresponde à quantidade de unidades cúbicas ocupadas pela figura e é sempre uma quantidade positiva.

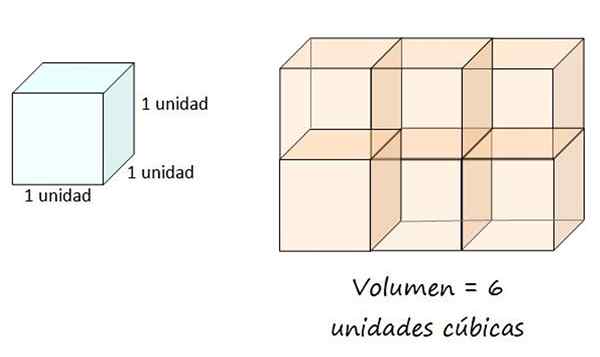Uma unidade cúbica é definida como o volume de um balde com borda igual a 1, então a caixa à direita tem um volume de 6 unidades cúbicas. Fonte: f. Zapata.

Volume de um corpo geométrico

Quando se trata de um corpo geométrico, como já mencionado, o volume é calculado através da fórmula apropriada, medindo as dimensões indicadas pela fórmula.

Por exemplo, se você quiser saber o volume de uma esfera, é necessário medir seu diâmetro e, com ele, seu raio é conhecido, que é metade. Se for uma caixa retangular, a largura, a altura e a profundidade do mesmo são medidas.

Em seguida, os valores solicitados na fórmula são inseridos, tomando cuidado para que todas as unidades sejam iguais, as operações necessárias são realizadas, existe o volume do objeto.

Volume de um corpo irregular

Sólidos irregulares não têm uma forma geométrica, como uma pedra ou uma piscadela. Mesmo assim, você pode encontrar seu volume com a ajuda de um recipiente graduado cheio de água, por meio do método de deslocamento líquido.

Em primeiro lugar, o volume ocupado pela água é determinado e, em seguida, o objeto irregular está completamente imerso, medindo o novo volume, que é maior que o original. O volume do objeto irregular é a diferença entre este volume e a da água sozinha.

Pode servir você: Genie Wiley, a garota selvagem que só reconheceu o nome dela

Para que esse método funcione, o objeto não deve ser feito de nenhuma substância que seja facilmente dissolvida na água, ele deve permanecer completamente submerso e, é claro, você deve ter um recipiente graduado do tamanho necessário para acomodá -lo completamente.

Exemplos de volume

O volume aproximado de alguns objetos conhecidos é:

• A Terra: 1.08321 × 10¹² km³
• Amazonas River: 225.000 m³/s (o volume por unidade de tempo é chamado de "fluxo")
• Grande pirâmide de Gizé: 2.600.000 m³
• Uma bola de futebol: 5600 cm³
• Uma mochila: 50 dm³

Volume e massa

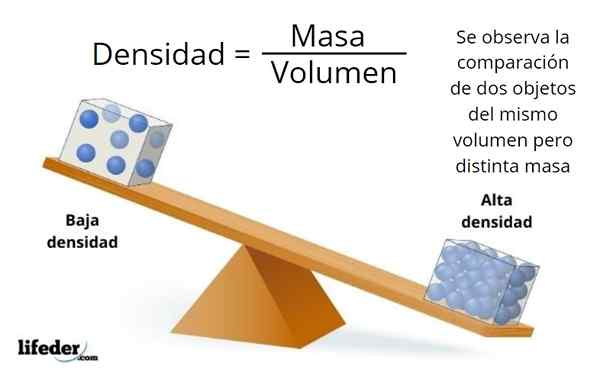
O volume e a massa não são sinônimos, o primeiro está ligado às dimensões do objeto e o segundo à quantidade de matéria que ele contém.

Pode haver muita matéria em um objeto de pequenas dimensões, ou muito pouco em um objeto grande, que depende da densidade do material, que é a razão entre a massa e o volume de um objeto:

Exercícios resolvidos

Exercício 1

Calcule o volume de uma caixa retangular cujas dimensões são 34 cm × 22 cm × 8 cm.

• Solução

O volume de uma caixa retangular é simplesmente o produto de suas três dimensões:

V = 34 cm × 22 cm × 8 cm = 5984 cm³

Exercício 2

A base de uma pirâmide quadrangular tem uma área de 16 cm² E sua altura é de 6 cm. Calcule o volume da referida pirâmide.

• Solução

A fórmula dada acima para o volume de uma pirâmide é usada, conhecida a área de sua base:

E valores numéricos são substituídos:

V = (1/3) × 16 cm² × 6 cm = 32 cm³