Características variáveis ​​contínuas, exemplos e exercícios

O Variável contínua É aquele que pode levar um número infinito de valores numéricos entre dois valores dados, mesmo que esses dois valores estejam arbitrariamente próximos. Eles são usados ​​para descrever atributos mensuráveis; por exemplo, altura e peso. Os valores assumidos por uma variável contínua podem ser números racionais, números reais ou números complexos, embora este último caso seja menos frequente em estatísticas. 

A principal característica das variáveis ​​contínuas é que entre dois valores racionais ou reais sempre podem ser encontrados, e entre o outro e o primeiro pode encontrar outro valor e tão indefinidamente.

figura 1. A curva representa uma distribuição contínua e as barras um discreto. Fonte: Pixabay

Por exemplo, suponha que a variável de peso em um grupo em que o maior peso tenha 95 kg e o menor peso de 48 kg; Esse seria o alcance da variável e o número de valores possíveis é infinito.

Por exemplo, entre 50,00 kg e 50,10 kg pode ser 50,01. Mas entre 50,00 e 50.01 a medida pode ser 50.005. Essa é uma variável contínua. Por outro lado, se no possível peso medidas, uma única precisão decimal foi estabelecida, a variável usada seria discreta.

Variáveis ​​contínuas pertencem à categoria de variáveis ​​quantitativas, porque têm um valor numérico associado. Com esse valor numérico, é possível realizar operações matemáticas que variam de aritmética aos métodos de cálculo infinitesimal. 

[TOC]

Exemplos

A maioria das variáveis ​​da física são variáveis ​​contínuas, entre elas podemos citar: comprimento, tempo, velocidade, aceleração, energia, temperatura e outros.

Variáveis ​​contínuas e variáveis ​​discretas

Nas estatísticas, vários tipos de variáveis ​​podem ser definidos, tanto qualitativos quanto quantitativos. Variáveis ​​contínuas pertencem a esta última categoria. Com eles, é possível executar operações de aritmética e de cálculo.

Por exemplo a variável h, correspondendo a pessoas com altura entre 1,50 me 1,95 m, é uma variável contínua. 

Vamos comparar essa variável com isso: o número de vezes que é caro no lançamento de uma moeda, que chamaremos n.

A variável n Você pode assumir valores entre 0 e o infinito, no entanto n Não é uma variável contínua, pois não pode levar o valor 1,3 ou 1,5, porque entre os valores 1 e 2 não há outro. Este é um exemplo de Variável discreta.

Exercício de variáveis ​​contínuas

Considere o seguinte exemplo: uma máquina produz fósforo corresponde e as embale em sua caixa. Duas variáveis ​​estatísticas são definidas:

Pode servir a você: Processo isobárico: fórmulas, equações, experimentos, exercícios

Variável 1: L = comprimento do plose.

Variável 2: n = número de porcos por caixa.

O comprimento das correspondências nominais é de 5,0 cm com uma tolerância a 0,1 cm. O número de porcos por caixa é 50 com uma tolerância de 3.

a) indicar a gama de valores que podem levar eu e N.

b) Quantos valores você pode tomar eu?

c) Quantos valores você pode tomar n?

Diga em cada caso se for uma variável discreta ou contínua.

Solução

Os valores de eu Eles são entendidos no intervalo [5,0-0,1; 5.0+0,1]; isto é, que o valor de eu está em intervalo [4,9 cm; 5,1 cm] e a variável eu Você pode tomar valores infinitos entre essas duas medidas. É então uma variável contínua.

O valor da variável n está no intervalo [47; 53]. A variável n Só pode levar 6 valores possíveis no intervalo de tolerância, é então uma variável discreta.

Exercício de distribuição de probabilidade

Se, além de ser contínuo, os valores tomados pela variável associaram uma certa probabilidade de ocorrência, então é um Variável aleatória contínua. É muito importante distinguir se a variável é discreta ou contínua, uma vez que modelos probabilísticos aplicáveis ​​um ao outro são diferentes.

Uma variável aleatória contínua é completamente definida quando os valores que eles podem assumir são conhecidos, e a probabilidade de que cada um deles tenha que acontecer.

-Exercício 1 de probabilidades

A fábrica de fósforos os faz de tal maneira que o comprimento dos paus está sempre entre os valores de 4,9 cm e 5,1 cm, e zero desses valores. Existe a probabilidade de obter um bastão que mede entre 5,00 e 5,05 cm, embora também possamos extrair um dos 5.0003 cm. Esses valores são igualmente prováveis?.

Pode atendê -lo: densidade relativa: cálculo, exemplos, exercícios

Solução

Suponha que a densidade de probabilidade seja uniforme. Em seguida, são listadas as chances de encontrar um fósforo com um certo comprimento:

-Que um fósforo está no intervalo [4,9; 5,1] tem probabilidade = 1 (ou 100%), uma vez que a máquina não tira correspondências desses valores.

-Encontrar um fósforo entre 4,9 e 5,0 tem probabilidade = ½ = 0,5 (50%), pois é metade da faixa de comprimentos.

-E a probabilidade de a partida ter comprimento entre 5,0 e 5,1 também é de 0,5 (50%)

-Sabe -se que não há bastões de fósforo que tenham um comprimento entre 5,0 e 5.2. Probabilidade: zero (0%).

Probabilidade de encontrar um bastão em um determinado intervalo

Agora vamos observar as seguintes probabilidades P para obter paus cujo comprimento está entre l₁ e eu₂:

 P = (L₂ -eu₁) /(EU_Máx - eu_min)

-P que uma partida tem um comprimento entre 5,00 e 5,05 é denotada como P ([5,00; 5.05]):

P ([5,00; 5,05]) = (5,05 - 5,00)/(5,1 - 4,9) = 0,05/0,2 = ¼ = 0,25 (25%)

-P que o Cerrillo tem comprimento entre 5,00 e 5.01 é:

P ([5,00; 5.01]) = (5,00 - 5,01)/(5.1 - 4,9) = 0,01/0,2 = 1/20 = 0,05 (5 %)

-P que o Cerrillo tem comprimento entre 5.000 e 5.001 é ainda menor:

P (5.000; 5.001) = 0,001/0,2 = 1/200 = 0,005 (0,5%)

Se continuarmos a diminuir o intervalo para se aproximar cada vez mais de 5,00, a probabilidade de um bastão ter exatamente 5,00 cm é zero (0%). O que temos é a probabilidade de encontrar uma correspondência dentro de um determinado intervalo.

Probabilidade de encontrar vários paus em um determinado intervalo

Se os eventos forem independentes, a probabilidade de que dois paus estejam em um determinado intervalo seja o produto de suas probabilidades.

-A probabilidade de dois paus estão entre 5,0 e 5,1 é 0,5*0,5 = 0,25 (0,25%)

-A probabilidade de que 50 paus estejam entre 5,0 e 5,1 é (0,5)^50 = 9 × 10^-16, que é quase nulo.

-A probabilidade de que 50 paus estejam entre 4,9 e 5,1 é (1)^50 = 1 (100%)

-Exercício 2 de probabilidades

No exemplo anterior, foi feita a suposição de que a probabilidade é uniforme no intervalo especificado, no entanto, nem sempre é o caso.

Pode servir a você: pressão hidrostática: fórmula, cálculo, exemplos, exercícios

No caso da máquina real que produz os paus, a possibilidade de que o bastão esteja no valor central seja maior do que em um dos valores extremos. Do ponto de vista matemático, isso é modelado com uma função f (x) conhecida como densidade de probabilidade.

A probabilidade de a medida estar entre a e b é calculada pela integral definida da função f (x) entre a e b. 

Como exemplo, suponha que queremos encontrar a função f (x), que representa uma distribuição uniforme entre os valores 4.9 e 5.1 do Exercício 1. 

Se a distribuição de probabilidade for uniforme, F (x) é igual a constante C, que é determinado tomando a integral entre 4,9 e 5.1 de C. Como essa integral é a probabilidade, o resultado deve ser 1.

Figura 2. Densidade de probabilidade uniforme. (Elaboração própria)

O que significa que C vale 1/0,2 = 5. Em outras palavras, a função de densidade de probabilidade uniforme é f (x) = 5 se 4.9≤x≤5.1 e 0 deste intervalo. A Figura 2 mostra uma função de densidade de probabilidade uniforme.

Observe como nos intervalos da mesma largura (por exemplo 0,02), a probabilidade é a mesma no centro que no final da faixa variável contínua eu (Comprimento de picles).

Um modelo mais realista seria uma função de densidade de probabilidade como o seguinte:

-f (x) = -750 ((x-5.0)^2-0,01) se 4.9≤x≤5,1

-0 fora deste intervalo 

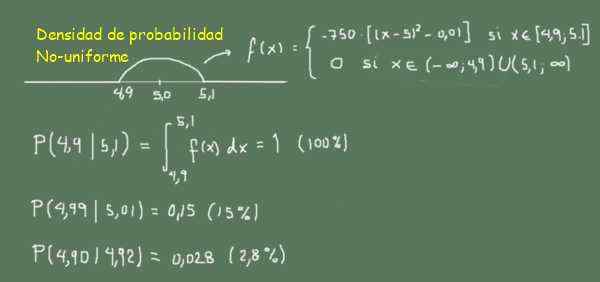Figura 3. Função de densidade de probabilidade não uniforme. (Elaboração própria)

Na Figura 3, pode ser observado como a probabilidade de encontrar palitos entre 4,99 e 5,01 (largura 0,02) é maior do que encontrar palitos entre 4,90 e 4,92 (largura 0,02)

Referências

1. Dinov, Ivo. Variáveis ​​aleatórias discretas e distribuições de probabilidade. Recuperado de: stat.UCLA.Edu
2. Variáveis ​​aleatórias discretas e contínuas. Recuperado de: OCW.mit.Edu
3. Variáveis ​​aleatórias discretas e distribuições de probabilidade. Recuperado de: Página inicial.DDMS.UIOWA.Edu
4. H. Peshro. Introdução à probabilidade. Recuperado de: Curso de Probabilidade.com
5. Mendenhall, w. 1978. Estatística para administração e economia. Grupo Editorial Americano Ibero. 103-106.
6. Problemas variáveis ​​e modelos de probabilidade aleatórios. Recuperado de: UGR.é.
7. Wikipedia. Variável contínua. Recuperado da Wikipedia.com
8. Wikipedia. Variável estatística. Recuperado da Wikipedia.com.