Características triângulos oblíquos, exemplos, exercícios

O Triângulos oblíquos Eles são aqueles que não têm ângulo reto, portanto nenhum de seus ângulos internos é igual a 90º. Então, um triângulo oblíquo pode ser Acutangle ou obtuso.

No primeiro caso, os ângulos internos do triângulo são agudos ou o mesmo: menos de 90º, enquanto no segundo, sempre há um ângulo maior que 90º, ou seja, um ângulo obtuso. Vejamos um exemplo de cada um na figura a seguir:

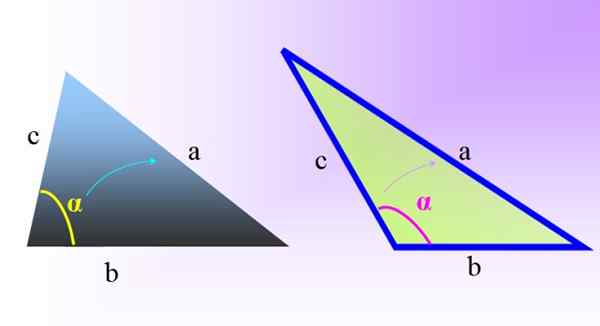figura 1. Triângulos oblíquos: à esquerda, um triângulo oblíquo e acutangle. À direita um triângulo oblíquo e obtuso. Fonte: f. Zapata.

Para encontrar os comprimentos dos lados e as medidas dos ângulos internos desse tipo de triângulos, na ausência de ângulos retos, não é possível aplicar o teorema de Pitágoras.

No entanto, existem alternativas para resolver o triângulo: os teoremas do cosseno e do seio e o fato de que a soma dos ângulos internos é igual a 180º.

[TOC]

Exemplos de Triângulos Oblicuágulos

Orientando -nos pela Figura 1, podemos reconhecer facilmente os triângulos oblíquos através de dois critérios que daremos abaixo.

Triângulo de Acutangle

Seja o triângulo dos lados a, b e c, com α o ângulo na frente do lado para.

Se o quadrado no lado oposto ao ângulo agudo α for menor que a soma dos quadrados dos lados restantes, o triângulo é acutangle. Algebricamente:

para² < b² + c²; α < 90º

O triângulo equilátero relativo, aquele que tem seus três lados da mesma medida, é acutangle e, portanto, oblíquo, uma vez que seus ângulos internos são iguais e medem 60º.

Triângulo obtuso

Por outro lado, se o quadrado do lado oposto para No ângulo obtuso α é maior que a soma dos quadrados dos outros dois, estamos na presença de um triângulo obtuso. Portanto:

para² > b² + c²; α> 90º

Por exemplo, um triângulo cujos ângulos internos são 105º, 60º e 15º é um triângulo oblíquo obtusa. Observe que 105º + 60º + 15º = 180º.

Teoremas do seio e cosseno

Para resolver os triângulos oblíquos, isto é, encontrar as medidas de todos os seus lados e todos os seus ângulos, os teoremas da mama e do cosseno são necessários.

Deixe A, B e C os lados de um triângulo e α, β e γ seus ângulos internos. Então:

Teorema da mama

O teorema da mama estabelece o seguinte:

Onde α é o ângulo oposto para o lado a, β é o ângulo oposto ao lado b e γ é o ângulo na frente do lado c.

Pode servir a você: Antiderivativo: fórmulas e equações, exemplos, exercícios

Equivalente:

Optamos por aplicar o teorema dos peitos quando vamos resolver um triângulo do que mais ângulos são conhecidos do que os lados.

Teorema de Coseno

De acordo com o teorema do Coseno:

c² = a² + b² - 2⋅A avô γ

Novamente o ângulo γ está na frente do lado c. Também podemos escrever expressões equivalentes para os lados A e B, como segue:

para² = b² + c² - 2⋅baloCOS α

E

b² = a² + c² - 2⋅a avô β

O teorema de cosseno é aplicado de preferência quando o valor de dois lados e o ângulo entre eles é conhecido. Além disso, uma vez que os três lados de um triângulo são conhecidos, o teorema nos permite calcular o cosseno do ângulo entre dois deles.

Exercícios resolvidos

- Exercício 1

Verifique se o triângulo cujos lados medem 20, 10 e 12 unidades arbitrárias é obtusa.

Solução

Não conhecemos nenhum dos ângulos internos, mas de acordo com os critérios que serve para reconhecer triângulos obtusos, podemos aumentar as desigualdades com os quadrados dos lados para observar se for cumprido.

Primeiro, encontramos os quadrados de cada lado:

vinte² = 400

10² = 100

12² = 144

E vemos isso de fato: 400> 100 + 144, desde 400> 244. Portanto, o triângulo contém um ângulo maior que 90º, localizado na frente do lado que mede 20. Consequentemente, este triângulo, além de ser oblíquo, também é obtuso.

- Exercício 2

Dado o triângulo oblíquo mostrado na Figura 2, cujas medidas são dadas em unidades arbitrárias, determine:

a) o valor de x. É um acutangen ou triângulo obtuso?

b) os ângulos internos restantes do triângulo

c) perímetro

d) Área.

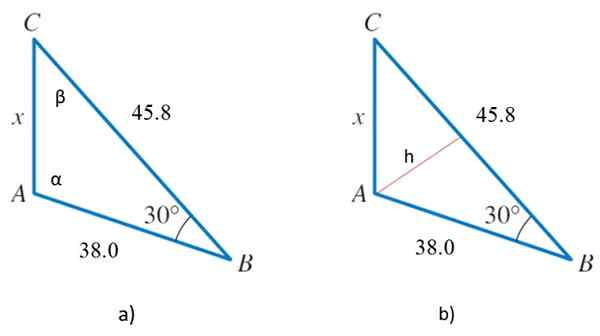Figura 2. 2a) Triângulo para o ano resolvido 2 e 2b) o mesmo triângulo com uma altura, que servirá para determinar a área. Fonte: f. Zapata.

Solução para

Do triângulo dois lados adjacentes são conhecidos, cujas medidas são 38.0 e 45.8 e o ângulo entre eles, que é 30º, portanto o teorema de cosseno é aplicado imediatamente:

x² = 38.0² + Quatro cinco.8² - 2 x 38.0 x 45.8 x cos 30º = 527.18

Portanto:

x = (527.18)^1/2 = 22.96

O desenho sugere que α> 90º e o triângulo é obtuso, além de oblíquo. Para verificar, encontramos os quadrados dos lados, como foi feito no exercício anterior:

22.96² = 527.18

38.0² = 1444.00

Quatro cinco.8² = 2097.64

O ângulo α é maior que 90º se for verdadeiro que o quadrado do lado oposto: 45.8²  É maior que a soma dos quadrados dos outros lados, que é 22.96² + 38.0².

Pode atendê -lo: leis de expoentes

Vamos ver se isso acontece:

527.18 + 1444.00 = 1971.2

Em efeito:

2097.64> 1971.2

Portanto, o ângulo α é maior que 90º.

Solução b

Agora podemos aplicar o teorema dos peitos para encontrar um dos ângulos que faltam. Vamos aumentá -lo para o ângulo β:

Sen 30º / 22.96 = sin β / 38

Sen β = 38 x (sen 30º / 22.96) = 0.8275

β = Arcsen (0.8275) = 55.84º

O ângulo que falta pode ser encontrado sabendo que a soma dos ângulos internos de qualquer triângulo é 180º. Portanto:

55.84º + 30º + α = 180º

α = 94.16º

Se preferir, você também pode usar o teorema de cosseno para encontrar o cosseno do ângulo que está entre dois lados adjacentes. Uma vez que a função Coseno Arc é usada para determinar o ângulo.

Os resultados podem diferir um pouco nas decimais, de acordo com o arredondamento realizado.

Solução c

O perímetro P é o contorno da figura, equivalente à soma das medidas dos três lados:

P = 22.96 + 38.00 + 45.80 = 106.76 unidades arbitrárias.

Solução d

A fórmula para calcular a área de qualquer triângulo é:

A = (1/2) x base x altura

Precisamos escolher um dos lados como base e determinar a altura. Por exemplo, escolher o lado que mede 45.8, nós desenhamos a altura h Até o vértice A, que é a linha vermelha na Figura 2b.

Ao fazer isso, dividimos o triângulo original em dois retângulos, ambos com h Como um cateto comum. Qualquer um deles serve, já que conhecemos um lado nítido e um ângulo.

Vamos levar aquele que tem hipotenusa igual a 38, uma categoria que mede h, qual é a altura procurada e o ângulo agudo igual a 30º.

Com a ajuda das razões trigonométricas do ângulo agudo 30º, determinamos o valor de h:

Sen 30º = cateto oposto a 30º / hipotenusa = h / 38

H = 38 x sen 30º = 19

Portanto:

A = (1/2) x 45.8 x 19 = 435.1 áreas arbitrárias de área.

Poderíamos ter escolhido outro lado como base, por exemplo, lado 38, nesse caso, a altura h É diferente, pois outro triângulo retângulo é formado, mas o resultado da área é o mesmo. Permanece como exercício para o leitor verificar.

- Exercício 3

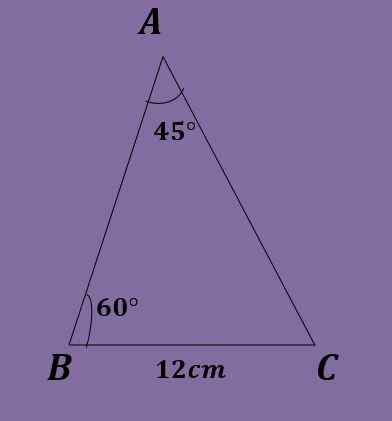
Dado um triângulo ABC que a = 45º, b = 60º e a = 12 cm, calcule os outros dados do triângulo.

Pode atendê -lo: sinais de agrupamento

Solução

Usando que a soma dos ângulos internos de um triângulo é igual a 180º, precisa:

C = 180º-45º-60º = 75º.

Os três ângulos já são conhecidos. Em seguida, passamos a usar o direito da mama para calcular os dois lados que estão faltando.

As equações que surgem são 12 / sem (45º) = b / sem (60º) = c / sem (75º).

Desde a primeira igualdade, você pode limpar "B" e obter isso:

b = 12*sem (60º)/sem (45º) = 6√6 ≈ 14.696cm.

Você também pode limpar "C" e entender:

C = 12*sin (75º)/sin (45º) = 6 (1+√3) ≈ 16.392cm.

- Exercício 4

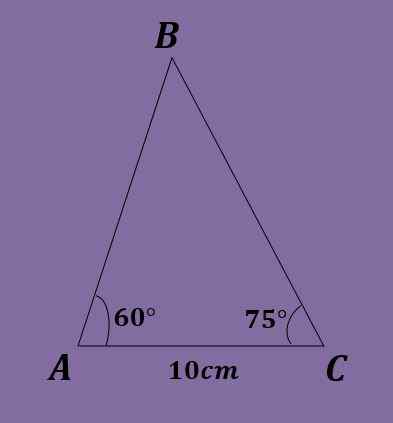
Dado o triângulo ABC de modo que a = 60º, C = 75º e B = 10cm, calcule os outros dados do triângulo.

Solução

Como no ano anterior você precisa B = 180º-60º-75º = 45º. Além disso, usando a lei da mama, você precisa / sem (60º) = 10 / sem (45º) = c / sem (75º), onde é obtido que a = 10*sem (60º) / sem (45º) = 5 √6 ≈ 12.247 cm e c = 10*sin (75º)/sem (45º) = 5 (1+√3) ≈ 13.660 cm.

- Exercício 5

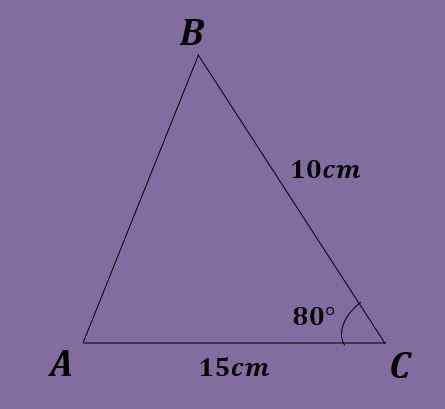
Dado o triângulo ABC de modo que a = 10cm, b = 15cm e c = 80º, calcule os outros dados do triângulo.

Solução

Neste exercício, apenas um ângulo é conhecido, portanto, não é possível começar como foi feito nos dois exercícios anteriores. Além disso, o direito da mama não pode ser aplicado porque nenhuma equação pode ser resolvida.

Portanto, a lei dos cosenos é aplicada. Você tem que:

C² = 10²+15² - 2 (10) (15) cos (80º) = 325 - 300*0.173 ≈ 272.905 cm,

Para que C ≈ 16.51 cm. Agora, conhecendo os 3 lados, a lei da mama é usada e obtém -se que:

10 / sem (a) = 15 / sem (b) = 16.51cm /sem (80º).

A partir daqui, quando claro b está sem (b) = 15*sem (80º)/ 16.51 ≈ 0.894, o que implica que B ≈ 63.38º.

Agora, pode -se obter que A = 180º - 80º - 63.38º ≈ 36.62º.

- Exercício 6

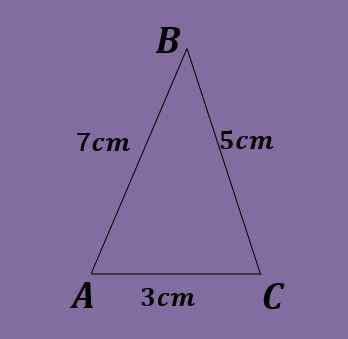
Os lados de um triângulo oblíquo são A = 5cm, B = 3cm e C = 7cm. Calcule os ângulos do triângulo.

Solução

Novamente, o direito da mama não pode ser aplicado diretamente, pois nenhuma equação serviria para obter o valor dos ângulos.

Usando a lei do cosseno, você deve c² = a² + b² - 2ab cos (c), de onde quando cos (c) = (a² + b² - c²)/ 2ab = (5² + 3² -7²)/ 2*5 *3 = -15/30 = -1/2 e, portanto, c = 120º.

Agora, o direito da mama pode ser aplicado e, portanto, obtém 5/sem (a) = 3/sem (b) = 7/sem (120º), onde b pode ser limpo B e obtê -lo sem (b) = 3* sem (120º )/7 = 0.371, de modo que B = 21.79º.

Finalmente, o último ângulo é calculado usando que A = 180º-133º-21.79º = 38.21st.

Referências

1. Clemens, s. Geometria com aplicações. Addison Wesley.
2. Ibáñez, p. 2010. Matemática III. Cengage Learning.
3. Jiménez, r. Matemática II: Geometria e Trigonometria. 2º. Edição. Pearson.
4. Matemática para você. Triângulo obtuso. Recuperado de: matemática para.WordPress.com.
5. Stewart, J. 2007. Pré -cálculo. 5 ª. Edição. Cengage Learning.