Propriedades, relacionamentos e fórmulas, exemplos, exemplos, exemplos

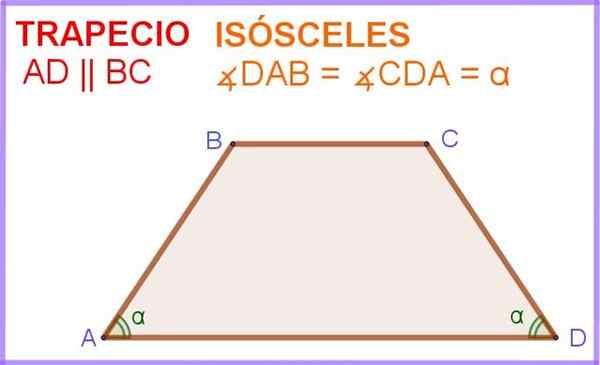
A trapézio isósceles É um quadrilateral no qual dois lados são paralelos entre si e também, os dois ângulos adjacentes a um desses lados paralelos têm a mesma medida.

Na Figura 1, você tem o quadrilateral ABCD, no qual os lados do AD e BC são paralelos. Além disso, os ângulos porte e porteDC adjacentes ao anúncio lateral paralelo têm a mesma medida α. 

figura 1. Isósceles de trapézio. Fonte: f. Zapata.

Assim, este polígono quadrilateral ou quatro a quatro é, na verdade, um trapézóide isósceles.

Em um trapézio, os lados paralelos são chamados bases e não paraléis são chamados lateral. Outra característica importante é o altura, que é a distância que separa os lados paralelos.

Além do trapézóide isósceles, existem outros tipos de trapézio:

-TRapeCio Escaleno, que tem todos os seus diferentes ângulos e laterais.

-TRetângulo RapeCio, em que um lado tem ângulos adjacentes retos.

A forma trapezoidal é frequente em várias áreas de design, arquitetura, eletrônica, cálculo e muito mais, como será visto mais tarde. Daí a importância de se familiarizar com suas propriedades.

[TOC]

Propriedades

Isoceles exclusivo trapézio

Se um trapézio for isósceles, atenda às seguintes propriedades características:

1.- Os lados têm a mesma medida.

2.- Os ângulos adjacentes às bases são os mesmos.

3.- Ângulos opostos são suplementares.

4.- As diagonais têm o mesmo comprimento, sendo o mesmo os dois segmentos que unem os vértices opostos.

5.- O ângulo formado entre as bases e as diagonais é a mesma medida.

6.- Tem circunferência circunscrita.

Reciprocamente, se um trapézio atender a alguma das propriedades anteriores, é um trapézóide isósceles.

Se em um trapézio isósceles um dos ângulos for reto (90º), todos os outros ângulos também serão, formando um retângulo. Isto é, um retângulo é um caso particular de isósceles trapézóide.

Figura 2. O recipiente de milho palomitas e as mesas da escola têm a forma de isósceles. Fonte: Pxfuel (à esquerda)/McDowell Craig através do Flickr. (certo)

Para todo trapézio

O seguinte conjunto de propriedades é válido para qualquer trapézio:

7.- O mediana do trapézio, esse é o segmento que se junta aos pontos médios de seus lados não paralelos, é paralelo a qualquer uma das bases.

8.- O comprimento da mediana é igual ao semi -súmeno (soma dividida por 2) da de suas bases.

9.- A mediana de um trapézio corta suas diagonais no ponto médio.

10.- As diagonais de um trapézio se cruzam em um ponto que os divide em duas seções proporcionais aos quocientes das bases.

onze.- A soma dos quadrados das diagonais de um trapézio é igual à soma dos quadrados de seus lados, além do produto duplo de suas bases.

Pode atendê -lo: quantos milésimos eles se encaixam em um décimo?

12.- O segmento que se junta aos pontos médios -diagonais tem comprimento igual à semi -referência das bases.

13.- Os ângulos adjacentes aos lados são suplementares.

14.- Um trapézio tem uma circunferência registrada se e somente se a soma de suas bases for igual à soma de seus lados.

quinze.- Se um trapézio tiver uma circunferência registrada, os ângulos com vértice no centro da referida circunferência e lados que passam pelas pontas do mesmo lado são ângulos retos.

Relacionamentos e fórmulas

O seguinte conjunto de relacionamentos e fórmulas é referido na Figura 3, onde, além do trapézio de isósceles, outros segmentos importantes já mencionados, como diagonais, altura e média.

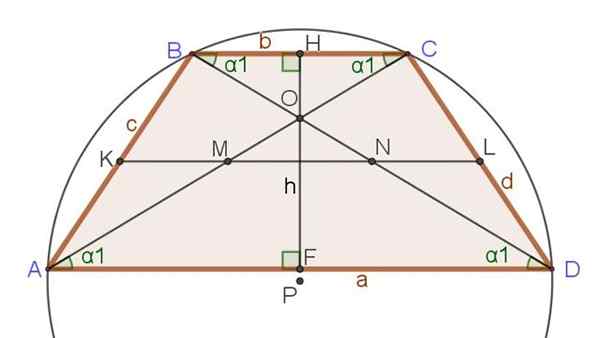Figura 3. Mediana, diagonais, altura e circunferência circunscrita em um trapézóide isósceles. Fonte: f. Zapata.

Relações exclusivas do isosceles TRAPECIO

1.- Ab = dc = c = d

2.- ∡dab = ∡cda e ∡abc = ∡bcd

3.- ∡dab + ∡bcd = 180º e ∡cda + ∡ABC = 180º

4.- Bd = ac

5.- ∡cad = ∡bda = ∡cbd = ∡bca = α₁

6.- A, B, C e D pertencem à circunferência circunscrita.

Relacionamentos para qualquer trapézio

7. Se Ak = Kb e DL = LC ⇒ KL || AD e KL || Bc

8.- KL = (AD + BC)/2

9.- AM = mc = ac/2 e dn = nb = db/2

10.- AO/OC = ad/bc y do/ob = ad/bc

onze.- AC² + DB² = Ab² + DC² + 2⋅ad⋅bc

12.- Mn = (AD - BC)/2

13.- ∡dab + ∡abc = 180º e ∡cda + ∡bcd = 180º

14.- Se ad + bc = ab + dc ⇒ ∃ r o que equidista de anúncio, bc, ab e dc

quinze.- Se ∃ r que equidista de anúncio, bc, ab e dc, então:

∡bra = ∡drc = 90º

Isoceles Relacionamentos trapézios com circunferência registrada

Se em um trapézio de isósceles a soma das bases é igual ao duplo de um lado, então há a circunferência registrada.

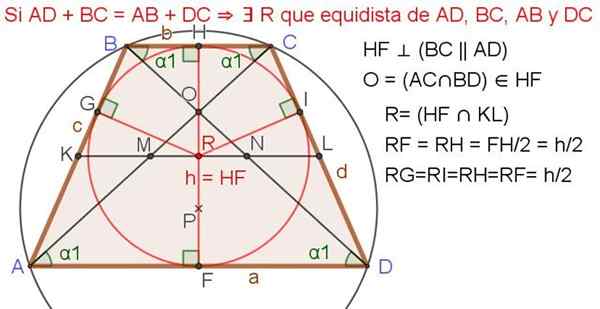Figura 4. Trapézio com circunferência registrada. Fonte: f. Zapata.

As propriedades a seguir se aplicam quando o trapézio de Isoceles tem uma circunferência registrada (veja a Figura 4 acima):

16.- Kl = ab = dc = (ad + bc)/2

17.- As diagonais são cortadas em ângulo reto: ac ⊥ bd

18.- A altura é a mesma que a mediana: hf = kl, isto é h = m.

19.- O quadrado da altura é igual ao produto das bases: H² = BC⋅AD

vinte.- Sob essas condições específicas, a área do trapezista é igual ao quadrado da altura ou ao produto das bases: área = h² = BC⋅AD.

Fórmulas para determinar um lado, conhecido as outras e um ângulo

Conhecida uma base, o lado e um ângulo, a outra base pode ser determinada por:

a = b + 2c cos α

B = a - 2c cos α

Se o comprimento das bases for conhecido como conhecido e um ângulo, os comprimentos de ambos os lados são:

Pode servir a você: Limite de Fermat: O que consiste e exercícios resolvidos

C = (a - b) / (2 cos α)

Determinação de um lado, conhecida os outros e uma diagonal

A = (D₁² - c²)/ B;

B = (D₁² - c²)/ para 

C = √ (D₁² - A⋅b)

Onde d₁ É o comprimento das diagonais.

Base da altura, da área e da outra base

a = (2 a)/h - b

b = (2 a)/h - a

De volta conhecidos nas bases, a área e um ângulo

C = (2a) /[(a + b) sin α]

Lateral conhecido a mediana, a área e um ângulo

C = a / (m.sin α)

Altura conhecida dos lados

H = √ [4 c² - (A - B)²]

Altura conhecida um ângulo e dois lados

H = tg α⋅ (a - b)/2 = c . sin α

Diagonais conhecidas de todos os lados, ou dois lados e um ângulo

d₁ = √ (c²+ a b)

d₁ = √ (A²+ c² - 2 a C cos α)

d₁ = √ (b² + c²- 2 b c cos β)

Perímetro do triângulo isósceles 

P = a + b + 2c

Área do trapézio de isósceles

Existem várias fórmulas para calcular a área, dependendo dos dados que são conhecidos. O seguinte é o mais conhecido, dependendo das bases e da altura:

A = h⋅ (a + b)/2

E esses outros também podem ser usados:

-Se os lados forem conhecidos

A = [(a +b)/4] √ [4c² - (A - B)²]

-Quando você tem dois lados e um ângulo

A = (b + c cos α) c sen α = (a - c cos α) c sen α α

-Se o raio da circunferência registrada for conhecida e um ângulo

A = 4 r² / Sin α = 4 r² / Sin β

-Quando as bases e um ângulo são conhecidos

A = a⋅b / sin α = a⋅b / sen β β 

-Se o trapézio puder ser registrado uma circunferência

A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b)/2

-Conhecidos as diagonais e ângulo que se formam

A = (D₁²/2) sen γ = (D₁² / 2) sen δ 

-Quando você tem o lado, a mediana e um ângulo

A = mc.sin α = mc.Sen β

Rádio de circunferência circunscrita

Somente isosceles trapézios têm uma circunferência circunscrita. Se a base principal for conhecida, o lado C e o diagonal D₁, Então o raio r da circunferência que passa pelos quatro vértices do trapézio é:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p -d₁)]

Onde p = (a + c + d₁) / 2

Exemplos de uso do trapézóide de isósceles

O trapezoidal de isósceles aparece no campo do design, como visto na Figura 2. E aqui temos alguns exemplos adicionais:

Em arquitetura e construção

Os incas antigos conheciam o trapézio isósceles e o usaram como um elemento de construção nesta janela de Cuzco, Peru:

Figura 5 . Janela com uma forma trapezoidal da coricancha, Cuzco. Fonte: Wikimedia Commons.

E aqui o trapézóide aparece novamente na chamada Folha trapezoidal, Um material frequentemente usado na construção:

Figura 6. Folha de metal trapezoidal protegendo temporariamente as janelas de um edifício. Fonte: Wikimedia Commons.

Em design

Já vimos que o trapézico de isósceles aparece em objetos do cotidiano, alimentos inclusivos como esta barra de chocolate:

Figura 7. Barra de chocolate cujos rostos têm a forma de isósceles. Fonte: Pxfuel.

Exercícios resolvidos

- Exercício 1

Um trapézio de isósceles é baseado em 9 cm, base inferior a 3 cm e suas diagonais 8 cm cada. Calcular:

Pode servir a você: Equação Geral de Parábola (Exemplos e Exercícios)

aparte

b) Altura

c) perímetro

d) ärea

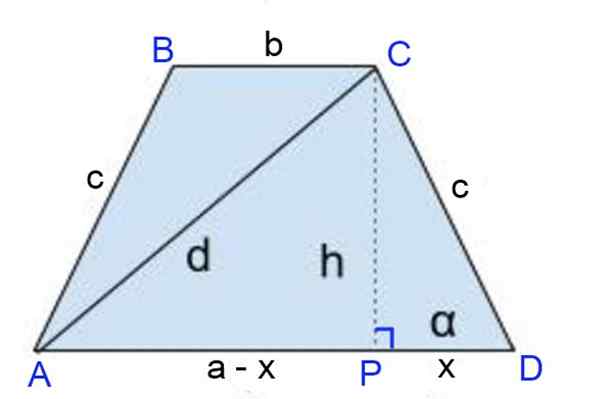Figura 8. Esquema para o Exercício 1. Fonte: f. Zapata

Solução para

A altura cp = h é desenhada, onde o pé da altura define os segmentos:

Pd = x = (a-b)/2 e 

AP = a - x = a - a/2 + b/2 = (a + b)/2.

Através do teorema de Pitágoras até o triângulo retângulo DPC:

c² = h² + (A - B)² /4

E também para o triângulo retângulo da APC:

d² = h² + AP² = h² + (A+b)² /4

Finalmente, um membro é subtraído, a segunda equação do primeiro e simplifica:

d² - c² = ¼ [(a+b)² - (A-b)²] = ¼ [(a+b+a-b) (a+b-a+b)]

d² - c² = ¼ [2a 2b] = a b

c²= d² - A b ⇒ c = √ (d² - a b) = √ (8² - 9⋅3) = √37 = 6,08 cm

Solução b

h² = d² - (A+b)² /4 = 8² - (12² / 2² ) = 8² - 6² = 28

H = 2 √7 = 5,29 cm

Solução c

Perímetro = a + b + 2 c = 9 + 3 + 2⋅6.083 = 24.166 cm

Solução d

Área = h (a+b)/2 = 5,29 (12)/2 = 31,74 cm

- Exercício 2

Há um trapézio isósceles cuja maior base é o dobro do menor e sua menor base é igual à altura, que é 6 cm. Determinar:

a) o lado do lado

b) perímetro

c) Área

d) ângulos

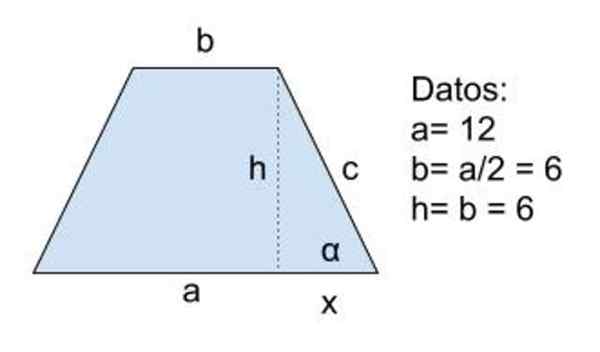Figura 8. Esquema para o Exercício 2. Fonte: f. Zapata

Solução para

Dados: a = 12, b = a/2 = 6 e h = b = 6

Prosseguimos dessa maneira: a altura h é desenhada e o teorema de Pitágoras é aplicado ao triângulo hipotenuse "C" e Catetos H e X:

c² = h²+XC²

Então você deve calcular o valor da altura dos dados (h = b) e o Cateto X: 

a = b + 2 x ⇒ x = (a-b)/2

Substituindo as expressões anteriores que você tem:

c² = b²+(A-b)²/2²

Agora os valores numéricos são introduzidos e simplificados:

c² = 62+ (12-6) 2/4

c² = 62 (1+¼) = 62 (5/4)

Obtenção:

C = 3√5 = 6,71 cm

Solução b

O perímetro p = a + b + 2 c

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Solução c

A área baseada na altura e comprimento das bases é:

A = h⋅ (a + b)/2 = 6⋅ (12 + 6)/2 = 54 cm²

Solução d

O ângulo α que forma o lado com a base principal é obtido por trigonometria:

Tan (α) = h / x = 6/3 = 2

α = arctan (2) = 63,44º

O outro ângulo, que forma o lado com a base menor, é β, que é suplementar de α:

β = 180º - α = 180º - 63,44º = 116,56º

Referências

1. E. PARA. 2003. Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
2. Campos, f. 2014. Matemática 2. Grupo editorial da Patria.
3. Libertado, k. 2007. Descubra polígonos. Companhia de Educação de Benchmark.
4. Hendrik, v. 2013. Polígonos generalizados. Birkhäuser.
5. Iger. Matemática Primeiro Semestre Tacaná. Iger.
6. Jr. Geometria. 2014. Polígonos. Lulu Press, Inc.
7. Miller, Heeren e Hornsby. 2006. Matemática: Raciocínio e Aplicações. 10º.  Edição. Pearson Education.
8. Patiño, m. 2006. Matemática 5. Editorial Progreso.
9. Wikipedia. Trapézio. Recuperado de: é.Wikipedia.com