Características de tiro parabólicas, fórmulas e equações, exemplos

Ele tiro parabólico Consiste em jogar um objeto ou projétil com um certo ângulo e deixá -lo se mover sob a ação da gravidade. Se a resistência do ar não for considerada, o objeto, independentemente de sua natureza, seguirá uma trajetória na forma de uma parábola.

É um movimento diário, uma vez que entre os esportes mais populares são aqueles em que bolas ou bolas são jogadas à mão, com o pé ou com um instrumento como uma raquete ou um morcego, por exemplo.

figura 1. O jato de água da fonte ornamental segue uma trajetória parabólica. Fonte: Wikimedia Commons. Zátonyi Sandor (IFJ.), Fizped/CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0)

Para estudar, o tiro parabólico é dividido em dois movimentos sobrepostos: um horizontal sem aceleração e o outro vertical com aceleração constante, que é a gravidade. Ambos os movimentos têm velocidade inicial.

Digamos que o movimento horizontal leva. Cada um desses movimentos é independente do outro.

Em vista do fato de que determinar a posição do projétil são os principais objetivos, é necessário escolher um sistema de referência apropriado. Os detalhes vêm a seguir.

[TOC]

Fórmulas e equações do tiro parabólico

Suponha que o objeto seja jogado com ângulo α em relação à velocidade horizontal e inicial v_qualquer como mostrado na figura abaixo à esquerda. O tiro parabólico é um movimento que ocorre no avião XY E nesse caso, a velocidade inicial se decompõe assim:

v_boi = v_qualquer cos α

v_Oy = v_qualquer sin α

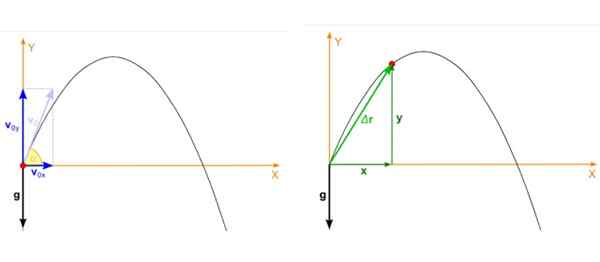Figura 2. À esquerda, a velocidade inicial do projétil e à direita a posição a qualquer momento do lançamento. Fonte: Wikimedia Commons. Zátonyi Sandor, (IFJ.) Fizped/CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0).

A posição do projétil, que é o ponto vermelho na Figura 2, a imagem direita, também tem dois componentes que dependem do tempo, um em x E o outro em e. A posição é um vetor que é indicado como r e suas unidades são de comprimento.

Pode atendê -lo: isomeria

Na figura, a posição inicial do projétil coincide com a origem do sistema de coordenadas, portanto x_qualquer = 0 e_qualquer = 0. Nem sempre é esse o caso, a origem pode ser escolhida em qualquer lugar, mas essa escolha simplifica muito os cálculos.

Quanto aos dois movimentos em x e y, são:

-X (t): é um movimento retilíneo uniforme.

-e (t): corresponde a um movimento retilíneo uniformemente acelerado com g = 9.8 m/s² e apontando verticalmente para baixo.

Em forma matemática:

x (t) = V_qualquer cos α.t

e (t) = V_qualquer .sin α.T - ½g.t²

O vetor de posição permanece:

r (t) = [v_qualquer cos α.t]Yo + [v_qualquer .sin α.T - ½g.t²] J

Nessas equações, o leitor atento notará que o sinal de menos se deve ao fato de que a gravidade aponta para o solo, o sentido escolhido como negativo, enquanto para cima é considerado positivo.

Como a velocidade é a primeira derivada da posição, é suficiente para derivar r (t) em relação ao tempo e obter:

v (t) = V_qualquer cos α Yo + (v_qualquer .sin α - Gt) J

Finalmente, a aceleração é expressa vetorialmente como:

para (t) = -g J

- Trajetória, altura máxima, tempo máximo e alcance horizontal

Trajetória

Para encontrar a equação explícita da trajetória, que é a curva y (x), você deve eliminar o parâmetro de tempo, limpando na equação para x (t) e substituindo em y (t). A simplificação é um tanto trabalhosa, mas finalmente é obtida:

Altura máxima

A altura máxima ocorre quando v_e = 0. Sabendo que existe o próximo relacionamento entre a posição e o quadrado da velocidade:

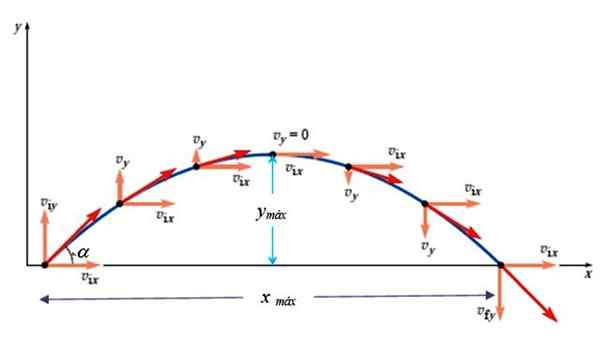Figura 3. A velocidade no tiro parabólico. Fonte: Giambattista, A. Física.

v_e² = v_Oy ²- 2GY

Fazendo v_e = 0 Apenas quando atinge a altura máxima:

0 = v_Oy ²- 2 g.e_máx → e_máx = v_Oy ²/2 g

Com:

Pode servir a você: aceleração centrípeta: definição, fórmulas, cálculo, exercícios

v_Oy = v_qualquer Senα

Tempo máximo

O tempo máximo é o tempo que o objeto leva para alcançar e_máx. Para calculá -lo, é usado:

v_e = v_qualquer .sin α - Gt

Sabendo que v_e É feito 0 quando t = t_máx, resultado:

v_qualquer .sin α - g.t_máx = 0

t_máx = v_Oy /g

Faixa horizontal máxima e tempo de vôo

O escopo é muito importante, porque indica onde o objeto cairá. Então, saberemos se dá ou não em branco. Para encontrar, precisamos de tempo de voo, tempo total ou t_v.

Da ilustração anterior, é fácil concluir que t_v = 2.t_máx. Mas a atenção só é verdade se o lançamento estiver no nível, ou seja, a altura do ponto de partida é a mesma que a altura da chegada. Caso contrário, o tempo está resolvendo a equação de segundo grau que resulta da substituição da posição final e_final:

e_final = v_qualquer .sin α.t_v - ½g.t_v²

De qualquer forma, o escopo horizontal máximo é:

x_máx = v_boi. t_v

Exemplos de tiro parabólicos

O tiro parabólico faz parte do movimento de pessoas e animais. Também de quase todos os esportes e jogos onde a gravidade intervém. Por exemplo:

Tiro parabólico em atividades humanas

-A pedra jogada por uma catapulta.

-O chute do gol do goleiro.

-A bola que joga o arremessador.

-A seta que sai do arco.

-Todos os tipos de saltos

-Jogue uma pedra.

-Qualquer arma de arremesso.

Figura 4. A pedra jogada pela catapulta e pela bola Patey na caixa de acabamento são exemplos de fotos parabólicas. Fonte: Wikimedia Commons.

O tiro parabólico na natureza

-A água brotando de jatos naturais ou artificiais como os de uma fonte.

-Pedras e lava brotando de um vulcão.

-Uma bola que salta na calçada ou uma pedra que faz na água.

-Todos os tipos de animais que saltam: cangurus, golfinhos, gazelas, felinos, sapos, coelhos ou insetos, para mencionar alguns.

Pode servir a você: poder mecânico: o que é, aplicações, exemplosFigura 5. O impala é capaz de pular para 3 m. Fonte: Wikimedia Commons. Arturo de Frias Marques/CC BY-S (https: // CreativeCommons.Org/licenças/BY-SA/3.0).

Exercício

Um gafanhoto formando um ângulo de 55 º com a horizontal e as terras em 0.80 metros depois. Encontrar:

a) A altura máxima atingida.

b) Se eu pulasse com a mesma velocidade inicial, mas formando um ângulo de 45º, seria mais alto?

c) O que pode ser dito do alcance horizontal máximo para este ângulo?

Solução para

Quando os dados fornecidos pelo problema não contêm a velocidade inicial V_qualquer Os cálculos são um pouco mais trabalhosos, mas das equações conhecidas, uma nova expressão pode ser deduzida. Partindo de:

x_máx = v_boi . t_voo = v_qualquer.cos α. t_v

Quando aterrissa mais tarde, a altura é 0 novamente, então:

v_qualquer .sin α.t_v - ½g.t_v²= 0

Como t_v É um fator comum, é simplificado:

v_qualquer .sin α - ½g.t_v= 0

Podemos limpar T_v Da primeira equação:

t_v = x_máx / v_qualquer.cos α

E substitua no segundo:

v_qualquer .sin α - (½g.x_máx / v_qualquer.cos α) = 0

Multiplicando todos os termos por v_qualquer.cos αA expressão não altera e o denominador desaparece:

(v_qualquer .sin α.) (v_qualquer.cos α) - ½g.x_máx = 0

v_qualquer² sin α. cos α = ½g.x_máx

Já pode ser limpo v_qualquer ou também substitua a seguinte identidade:

Sen 2α = 2 sen α. cos α → v_qualquer² Sen 2α = g.x_máx

Calcula-se v_qualquer²:

v_qualquer² = g.x_máx / Sen 2α = (9.8 x 0.8 / sen 110) m²/s² = 8.34 m²/s²

E finalmente a altura máxima:

e_máx= v_Oy ²/2g = (8.34 x sen² 55)/(2 x 9.8) M = 0.286 m = 28.6 cm

Solução b

A lagosta consegue manter a mesma velocidade horizontal, mas quando o ângulo diminui:

e_máx= v_Oy ²/2g = (8.34 x sen² 45)/(2 x 9.8) M = 0.213 m = 21.3 cm

Atinge uma altura menor.

Solução c

O escopo horizontal máximo é:

x_máx = v_qualquer² Sen 2a / g

Quando o ângulo varia, o escopo horizontal também muda:

x_máx = 8.3. 4 Sen 90 / 9.8  M = 0.851 m = 85.1 cm

O salto está mais longo agora. O leitor pode verificar se é máximo para o ângulo de 45 º então:

sin 2α = sin 90 = 1.

Referências

1. Figueroa, d. 2005. Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
2. Giambattista, a. 2010. Física. Segunda edição. McGraw Hill.
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Resnick, r. 1999. Físico. Vol. 1. 3ª ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V.
5. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1.