Tipos de funções e seus gráficos

Existem diversos Tipos de funções que são usados ​​para modelar problemas em ramos de conhecimento, como ciências naturais, administração, economia e ciências sociais. Matematicamente falando, uma função é uma relação entre duas ou mais variáveis.

Muitas vezes, certos objetos ou quantidades estão relacionados entre si. Esses valores são representados por variáveis. Por exemplo, existem duas variáveis ​​relacionadas, pertencentes a dois conjuntos A e B, não necessariamente numéricos, embora na maioria das vezes sejam-.

Para ser considerado uma função, esse relacionamento deve atender a duas condições: a primeira é que todos os elementos do conjunto inicial para participar e o segundo, que cada elemento do referido conjunto está relacionado a apenas um dos elementos do conjunto B.

Variáveis ​​geralmente são chamadas com letras x e e, com x como a variável independente e e como a variável dependente. Naturalmente, eles podem ser chamados de qualquer outra maneira, escolhendo o nome da variável de acordo com a magnitude que ela representa.

A relação entre os dois é denotada através da carta F -ou outra letra do alfabeto-e é representada de várias maneiras, como um conjunto de pares ordenados, um gráfico, uma expressão verbal ou uma fórmula algébrica:

• f (x) = x + 1
• População p de uma certa cidade em um certo intervalo de tempo t.
• H (x) = (1,3); (2,4); (3,5); (4.6)

As funções são caracterizadas por ter domínio e alcance ou rota. Domínio é o conjunto de valores que a variável x Você pode tomar, enquanto o intervalo é o conjunto de valores que adquire a função ou variável dependente e.

Classificação de funções

As funções podem ser agrupadas em 5 grandes categorias, como refletido no seguinte esquema, no qual cada grupo é rotulado com um número romano e uma cor. A partir da esquerda para a direita, as funções são classificadas de acordo com:

• I) sua forma.
• Ii) simetria.
• Iii) a maneira de expressar a variável.
• Iv) sua continuidade e monotonia.
• V) a maneira como os elementos do domínio estão relacionados aos do intervalo.

Critérios principais de classificação para funções. Fonte: f. Zapata.

Agora siga uma breve descrição de cada um dos tipos de funções com seus respectivos exemplos.

I) funções de acordo com sua forma

Yo.1) funções algébricas

Eles estão entre as funções mais usadas em vários campos da ciência e, portanto, são os mais conhecidos. Eles são caracterizados por ter como regra de correspondência, uma expressão algébrica.

Por sua vez, as funções algébricas são subdivididas nos seguintes tipos:

• Yo.1.a) polinomial ou polinomial.
• Yo.1.b) racional.
• Yo.1.c) Irracional.
• Yo.1.d) por seções.

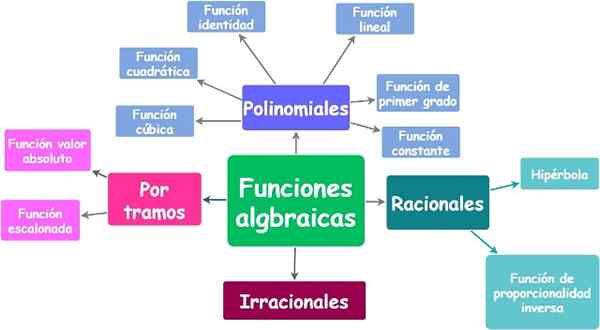Funções algébricas e seus tipos. Fonte: f. Zapata.

Yo.1.a) funções polinomiais ou polinomiais

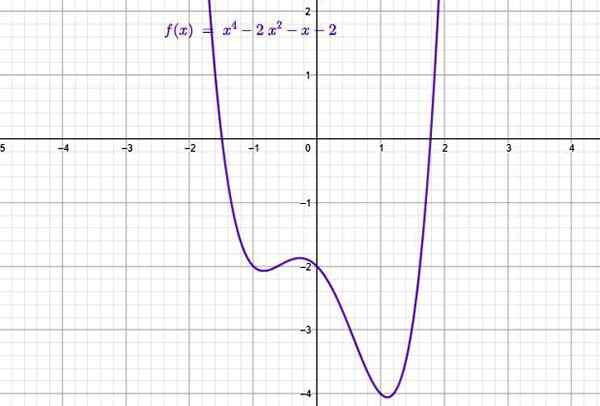Exemplo de função do tipo polinomial. Fonte: f. Zapata através da Geogebra.

Eles consistem em somas de termos cuja forma geral é:

P (x) = a_nxⁿ + para _N-1x^N-1 +… para₁x + a₀

Onde os coeficientes para_n, para _N-1… para₁, para₀ Eles são números reais e n é um número inteiro. O domínio das funções polinomiais é o conjunto de números reais e também são funções contínuas em todo esse domínio.

Na figura superior está o gráfico da seguinte função polinomial da Ordem 4:

f (x) = x⁴ - 2x² - x -2

Entre as funções polinomiais, alguns casos particulares são distinguidos, de acordo com os valores dos coeficientes. Vale a pena considerar com cuidado, porque eles são muito úteis em várias situações:

i) função constante

Há uma função constante quando todos os coeficientes são cancelados, exceto₀:

f (x) = a₀ = k

O gráfico da função constante é uma linha reta paralela ao eixo horizontal, como linhas:

• f (x) = 2
• g (x) = π
• H (x) = -3/2

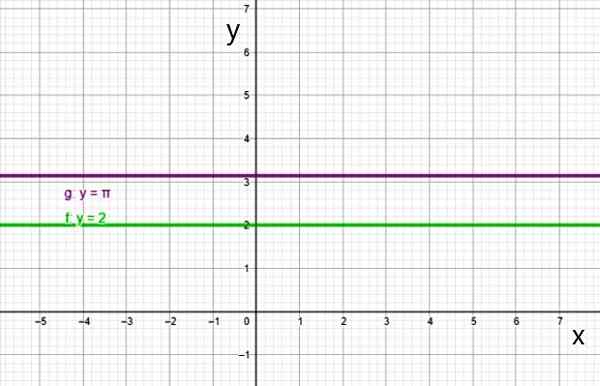Dois exemplos de função constante. Fonte: f. Zapata.

Ii) Função de primeiro grau

A primeira função -graus ou função relacionada é que cujo gráfico é uma linha reta. É um caso particular da função polinomial em que todos os coeficientes do anular₁ já₀. É dado por:

f (x) = a₁x + a₀

O valor a₁ É a inclinação da linha, que dá uma medida de sua inclinação, e₀ É o corte da linha com o eixo vertical. Ambos podem levar valores positivos ou negativos.

Exemplos de função de primeiro grau são os seguintes:

• G (x) = 2x -1
• H (x) = -6x +5/2

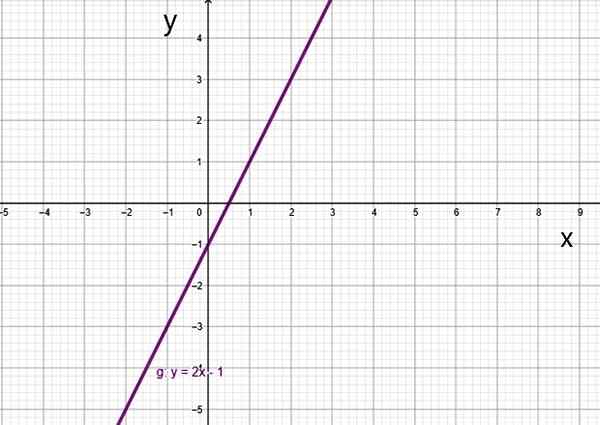Função de primeiro grau F (x) = 2x-1. Fonte: f. Zapata.

Há um caso especial, que é a função linear.

Pode atendê -lo: medidas de tendência central para dados agrupados: fórmulas, exercícios

iii) função linear

Quando o coeficiente para₀ É 0, a função sempre passa pela origem e é expressa por f (x) = a₁X, chamando Função linear, Como vai:

• f (x) = 5x
• G (x) = -7x

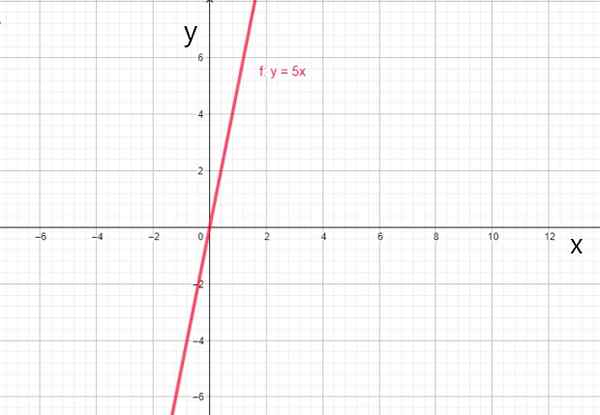Função linear F (x) = 5x. Fonte: f. Zapata.

iv) Função de identidade

É um caso particular da função linear, na qual₁ = 1:

f (x) = x

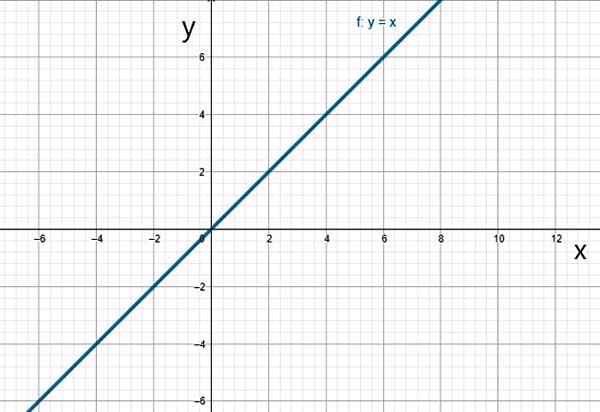A função de identidade. Fonte: f. Zapata.

v) função quadrática

Tem a forma geral:

f (x) = a₂x² +para₁x + a₀

Com um₂  ≠ 0.

Seu gráfico é uma parábola cujo eixo axial ou de simetria é paralelo ao eixo das ordenadas. Sempre cruza o eixo vertical no ponto de coordenada x = 0, y = a₀. Quanto às interseções com o eixo horizontal, pode ter até um máximo de 2.

Exemplos de funções quadráticas são:

• f (x) = x² - 3x - 4
• G (x) = 4x²
• H (x) = x²-1

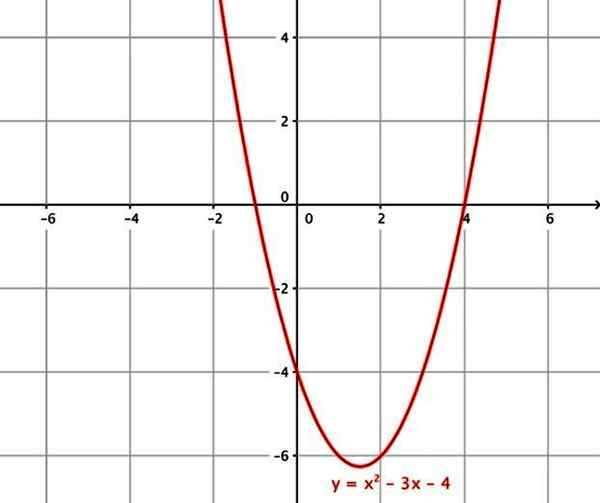A função quadrática. Fonte: Wikimedia Commons.

vi) Função cúbica

Como o nome indica, a função cúbica contém um poder de 3:

f (x) = a₃x³ + para₂x² + para₁x + a₀

O coeficiente a₃ É sempre diferente de 0, como nesses casos:

• f (x) = x³
• G (x) = 5x³ - 2
• H (x) = -3x³ + 4x² + 10x + 1

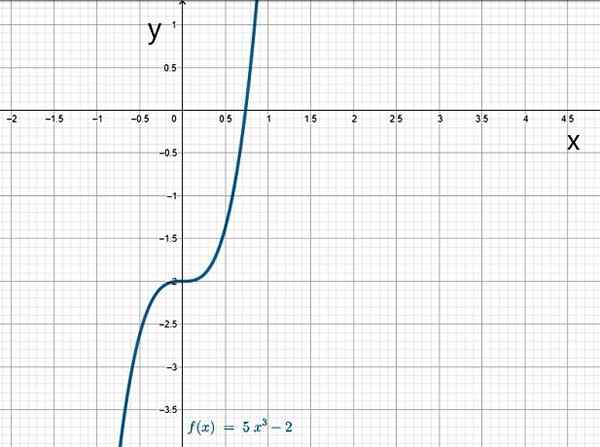Função cúbica. Fonte: f. Zapata.

Yo.1.b) Funções racionais

As funções racionais têm o formulário:

 Onde p (x) e q (x) são polinômios irredutíveis, ou seja, eles não têm fator comum e, em qualquer caso, q (x) ≠ 0.

A partir do domínio das funções racionais, todos os valores que anulam o denominador q (x), ou seja, suas raízes, enquanto os valores dos valores dos valores dos valores de e que determinam as assíntotas horizontais.

Uma assíntota é uma linha para a qual a função está se aproximando, tanto à esquerda quanto à direita, acima ou abaixo, mas nunca cruza. Essas linhas podem ser verticais, horizontais ou inclinadas.

Exemplos de funções racionais são:

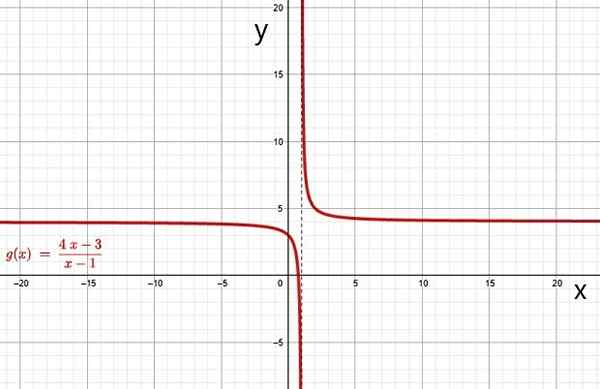Função racional. Fonte: f. Zapata através da Geogebra.

i) Hiperbola

O gráfico de uma função racional é uma hipérbole quando o polinômio no denominador q (x) tem grau 1. O gráfico das funções f (x) e g (x) dos exemplos acima são hiperbolas, pode ser facilmente verificado por meio de um software gráfico online gratuito, como geogebra.

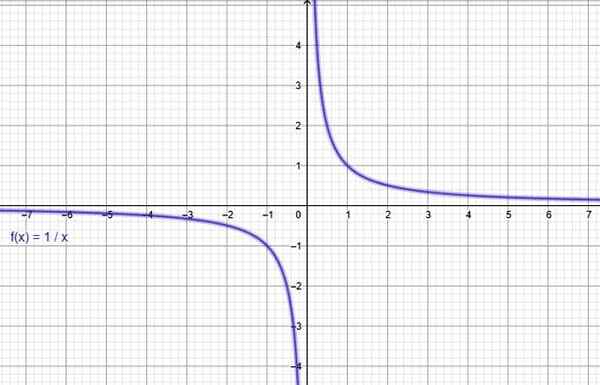A função y = 1/x. Fonte: f. Zapata através da Geogebra.

Ii) Função de proporcionalidade inversa

É uma função da forma:

Onde C é um número real diferente de 0. Seu domínio é o conjunto de números reais, exceto 0.

Yo.1.c) Funções irracionais

São aqueles cuja variável independente está sob um sinal radical. Sua forma geral é:

Algumas dessas funções podem ser:

• 
• 

O domínio dessas funções é determinado da seguinte forma:

-Se as raízes forem do índice de torque, a quantidade sub -naadical f (x) deve ser sempre 0 ou positiva.

-Quando as raízes são estranhas, f (x) pode ser positivo ou negativo. Portanto, neste caso, o domínio da função é os números reais.

Por exemplo, o domínio de:

É o conjunto de números reais de modo que X-3 é maior ou igual a 0. Nesse caso, x deve ser maior ou igual a 3. Portanto, o domínio desta função é o conjunto de valores do intervalo [3, ∞+).

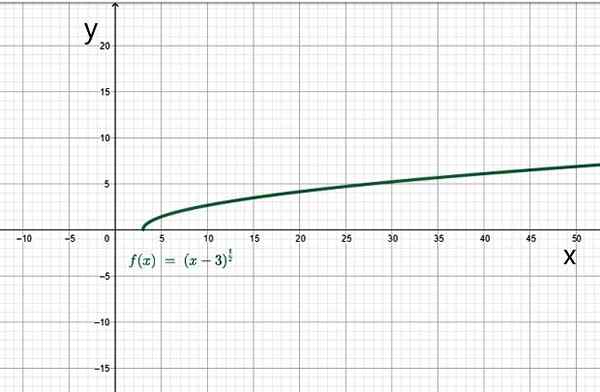 Exemplo de função irracional. Fonte: f. Zapata.

Yo.1.d) funções em pedaços ou por seções

A função em partes, por seções ou peças é aquela que requer mais de uma fórmula para diferentes valores de domínio. Aqui estão alguns exemplos de seu aplicativo:

-Taxas para enviar pacotes por correio, dependendo do peso ou volume, origem e destino do mesmo.

-Taxas de serviços, por exemplo, telefonia e eletricidade.

-Venda de ingressos para museus ou parques de diversões, dependendo da idade.

Na forma matemática, uma função em partes pode ser, por exemplo:

O domínio de uma função em partes depende de sua definição. No exemplo anterior, o domínio é o conjunto formado por: (-∞, -1) ∪ [1,+∞).

A função de valor absoluto. Fonte: f. Zapata através da Geogebra.

Ii) função escalonada

O gráfico desta função por seções consiste em etapas, como as de uma escada ou pode ser de diferentes alturas, dependendo da maneira como a função é definida.

Pode atendê -lo: Hipparco de Nicea: Biografia e Contribuições para a Ciência

Para isso, um intervalo finito [a, b] é escolhido que contém um certo número finito de descontinuidades, chamado x_Yo < x₁ < x₂ <… . x_n  E um intervalo aberto é escolhido (x_Yo , x_I+1) Para dar uma constante de valor S_Yo, Com os saltos nos pontos x_Yo. O valor de S_Yo É a altura do passo em questão.

Um exemplo de uma função escalonada é a parte inteira, que leva qualquer número e a associa ao seguinte número inteiro, seja por excesso ou por padrão. O seguinte é uma parte inteira:

[x] = (maior número inteiro ≤ x)

De acordo com esta função, toda a parte de 2.5 é:

[2.5] = (maior número inteiro ≤ 2.5) = 2

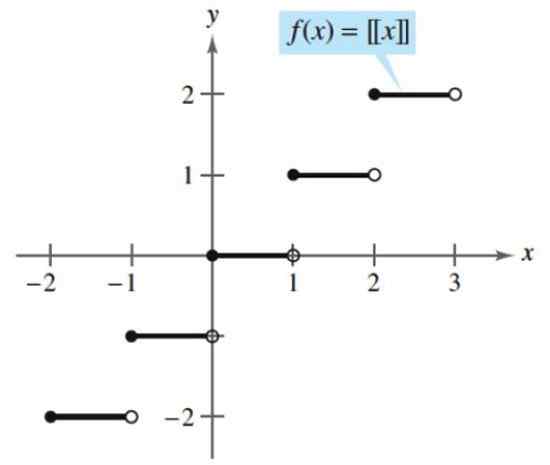Toda a parte de. Fonte: Larson, R. Cálculo com geometria analítica. McGraw-Hill.

Yo.2) funções transcendentes

Funções não algébricas são chamadas de transcendentes. As funções exponenciais, logarítmicas e trigonométricas são funções transcendentes.

Neles a variável x Faz parte do argumento da função ou como parte do expoente ou do índice de alguma raiz, por exemplo:

• f (x) = log (x+1)
• H (x) = -0.2⋅8^-3x

As funções transcendentes têm muitas aplicações, por exemplo, no estudo de vibrações e ondas, distribuições de probabilidade, modelagem das ondas, crescimento de diversas populações, decaimento radioativo, taxas de juros e muito mais mais. 

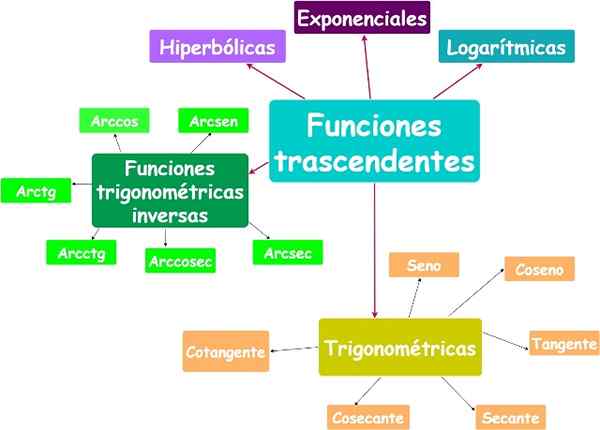Principais funções transcendentes. Fonte: f. Zapata.

Yo.2.a) Função exponencial 

A função exponencial é definida por:

f (x) = a^x

Onde a é a base, que é sempre um número positivo de 1, e a variável, um número real, aparece no expoente. Em geral, a função exponencial está escrita:

f (x) = a⋅a^Bx

Aqui A e B são coeficientes reais. A seguir, são as funções deste tipo:

• f (x) = 5e^x
• H (x) = 4. 10^5x
• g (t) = 8e^-2t

A base e, onde e É o número de Euler 2.71828 ..., freqüentemente aparece em problemas de ciência e engenharia, bem como estatísticas. Quando a função tem esta base é chamada Função exponencial natural.

O domínio da função exponencial é o conjunto de números reais, enquanto o intervalo é o número positivo.

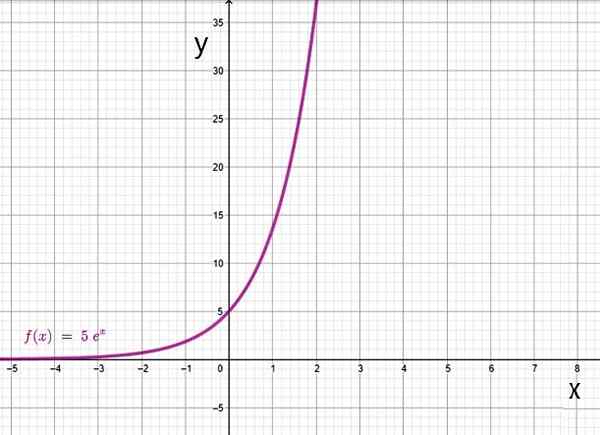Função exponencial com base em. Fonte: f. Zapata através da Geogebra.

Yo.2.b) Função do logaritmo

Por sua parte, a função do logaritmo com base em para É a função inversa da função exponencial com base em para. Sim:

registro_para x = y

Então:

x = a^e

Em particular, se a base do logaritmo for o número e, a função é chamada Função do logaritmo neperiano E é denotado como ln. As funções deste tipo são:

• f (x) = ln x
• g (x) = log (x+1)
• H (t) = 1 - log x²

O domínio da função logaritmo, independentemente da base, são os números reais positivos, sem incluir o 0. Isto é, não há logaritmos de números negativos ou 0.

No entanto, um logaritmo pode ser 0 ou negativo: o logaritmo do número entre 0 e 1 é negativo e, por sua parte, alcança_para 1 = 0.

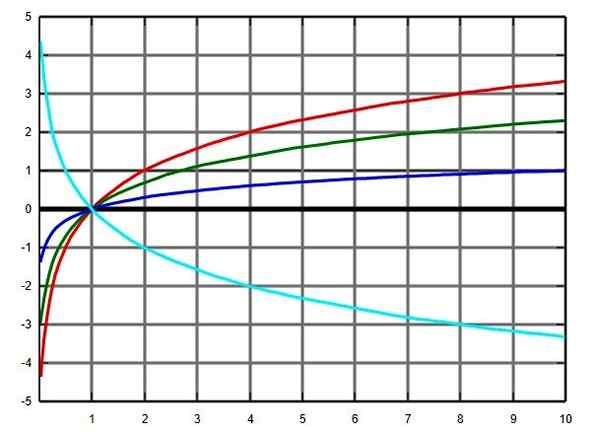Gráfico da função logaritmo em várias bases: base 2 em vermelho, verde e, azul -Base e turquesa na base 0.5. Fonte: Wikimedia Commons.

Yo.2.c) funções trigonométricas

São aqueles que vêm das razões trigonométricas: seio, cosseno, tangente, secagem, harmonia e cotangente de um ângulo x. Eles são denotados respectivamente como:

Sen x, cos x, tg x, seg x, danos x e cotg x

São funções periódicas, o que significa que sua forma é repetitiva, por isso são muito úteis para descrever fenômenos naturais, como sinais, oscilações, movimento circular e movimentos de balanço, que são caracterizados por serem repetitivos.

Exemplos de funções trigonométricas são:

• f (x) = sin x
• G (t) = 5⋅Cos (ωt + π)
• H (x) = TG (X/2)

A variável x é expressa em Radianes.

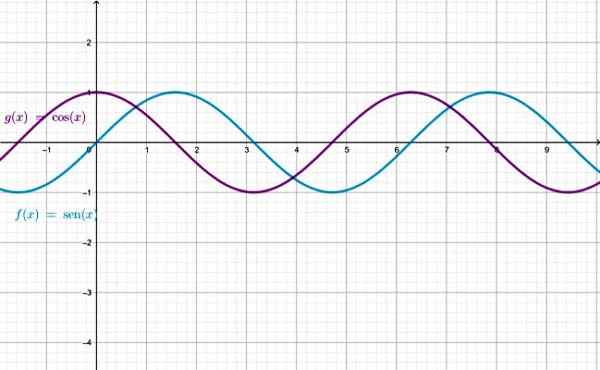Gráfico das funções sen x e cos x, observe que elas são idênticas, exceto que uma é deslocada em relação ao outro. Fonte: f. Zapata através da Geogebra.

O domínio das funções sen x e cos x é o conjunto de números reais. Para as funções restantes, existem X valores para os quais a função não está definida:

-A função TG X não existe quando x = ± π /2, ± 5π /2 ... Isto é, todos os múltiplos ímpares de π /2.

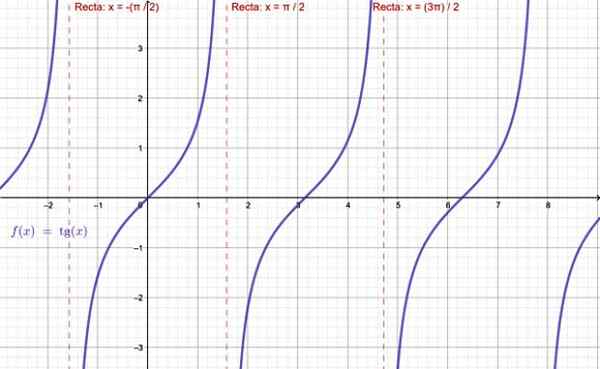Gráfico da função tangente. Fonte: f. Zapata através da Geogebra.

-Quanto a f (x) = cotg x, esta função não é definida para todos os múltiplos de π: ± π, ± 2π, ± 3π ..

Pode atendê -lo: Lei dos Sinais

-A função y = seg x não é válida quando cos x = 0, que exclui x = ± π /2, ± 5π /2… de seu domínio.

-Finalmente, para f (x) = dano x, todos os múltiplos de π não pertencem ao seu domínio.

Yo.2.d) funções hiperbólicas

Funções hiperbólicas são combinações especiais de exponencial e^x e e^-x E eles são chamados de seio, Coseno .. .hiperbólico. Como nas funções trigonométricas, também chamadas de "circular", existem 6 funções hiperbólicas:

-Seio hiperbólico Sen X:

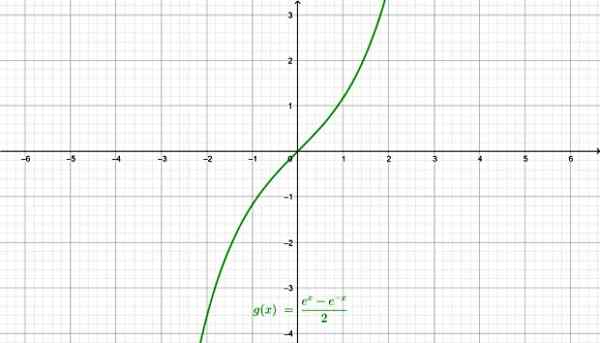A função do seio hiperbólico. Fonte: f. Zapata através da Geogebra.

-Cosseno hiperbólico Cosh x:

 -Tangente hiperbólica Tanh x:

 -Harvester hiperbólico CSCH X:

 -Secante hiperbólico Sech X:

-Cotangente hiperbólico Coth X:

Um cabo flexível, feito de material uniforme e suspenso entre dois pontos, assume a forma de uma curva chamada catenária, que é expresso como um cosseno hiperbólico:

Yo.2.e) funções trigonométricas inversas

Eles correspondem ao inverso das funções trigonométricas. Por exemplo, qual seria o ângulo (arco) cujo seio vale 0.5?

A resposta é arco sen 0.5, que diz “Arco sinusal de 0.5 ”, e esse ângulo é 30º, embora em princípio, este não seria o único ângulo cujo peito vale 0.5, já que a função sen x é periódica. O que acontece é que, se a função Sen X for tirada em todo o seu domínio, não teria inverso, de modo que a função Arcoseno não pudesse ser definida. A questão é resolvida restringindo tudo aos ângulos entre -π/2 e +π/2.

Isso pode ser expresso da seguinte maneira:

Se arco sen x = θ, significa que sin θ = x

Com -π/2 ≤ θ ≤ π/2.

Outra notação usada para arco sen x é f (x) = sin^-1 x. O gráfico é mostrado abaixo:

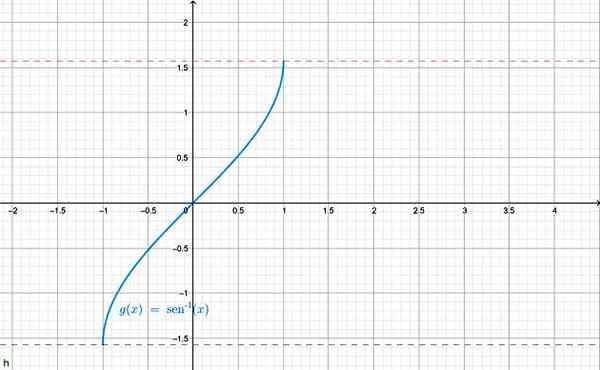Gráficos da função arcsen x. Fonte: f. Zapata através da Geogebra.

Também é possível definir inverso para as outras funções trigonométricas, por exemplo: arc cos x = θ e assim. Para cada um, a classificação é restrita adequadamente, para ser o inverso da função trigonométrica correspondente.

Ii) funções de acordo com sua simetria

Ii.1) par

Se para todos os X pertencentes ao domínio de f (x), é cumprido que:

f (x) = f (-x)

Dizem que a função é uniforme, como os que se seguem:

• f (x) = x² - 3
• g (x) = cos x
• 

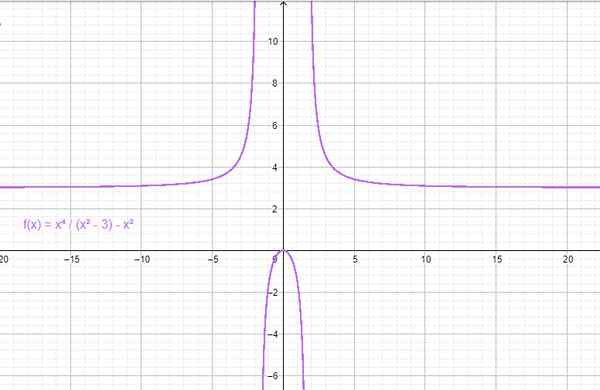  Exemplo de uma função de par. Fonte: f. Zapata através da Geogebra.

Por exemplo, fazendo x = 1 em f (x) = x² - 3 se obtem:

f (1) = 1² - 3 = -2.

E se x = -1, então:

f (-1) = (-1)² - 3 = -2.

Ambos os resultados são idênticos.

As funções uniformes têm simetria em torno do eixo vertical, como pode ser visto na figura anterior.

Ii.2) Função ímpar

Por outro lado, sim:

f (-x) = -f (x)

A função é estranha.

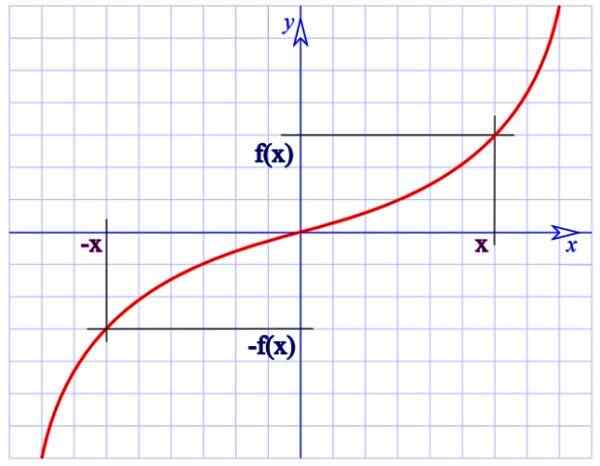Uma função estranha. Fonte: Wikimedia Commons.

Por exemplo, a função f (x) = 1/x da figura superior é ímpar, pois:

f (-x) = -1/x

E

-f (x) = -1/x

Outra função importante importante é f (x) = sin x x.

Observe que as funções ímpares têm simetria de rotação de 180º em torno da origem (o gráfico não é alterado se cada ponto for girado 180º em relação à origem das coordenadas).

Iii) função de acordo com a expressão da variável

Iii.1) funções explícitas

Eles são expressos diretamente em termos da variável dependente, como y = f (x). Por exemplo:

• f (x) = x³

Iii.2) funções implícitas

Nas funções implícitas, nenhuma das variáveis ​​parece clara. Eles são expressos como f (x, y) = 0, como:

• x² + e² -3xy = 0
• xy = - x²+ X-5

As funções descritas ao longo deste artigo são funções explícitas.

Iv) Funções de acordo com seus gráficos

De acordo com o gráfico, as funções podem ser contínuas ou descontínuas. Funções contínuas podem ser rastreadas sem interromper o golpe, por outro lado, funções descontínuas apresentam saltos. Na imagem a seguir, a função é descontínua em x = a:

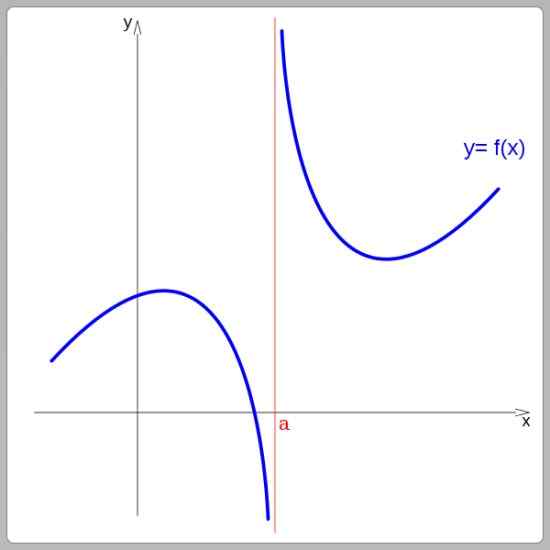Função de descontinuidade em x = a. Fonte: Wikimedia Commons.

Exemplos de funções contínuas são função linear, função quadrática e funções seno. E entre as funções descontínuas estão a função escalonada e a função tangente.

V) funções de acordo com a relação entre os elementos do domínio e o intervalo

V.1) Função injetiva

Uma função é Injetivo Quando não há dois elementos diferentes no conjunto inicial ou de domínio, que têm a mesma imagem no conjunto de chegada.

Suponha que as funções reais tenham, a menos que especificado de outra forma, por exemplo:

f (x) = 5x -2

Todo o valor x pertencente ao domínio de f (x), que é o conjunto ℛ dos números reais, tem uma imagem única e também real. Por outro lado, nesta outra função:

g (x) = x²

Existem elementos diferentes no domínio que têm a mesma imagem, por exemplo x₁= 2 e x₂= -2:

G (2) = g (-2) = 4.

A maneira de identificar uma função injetiva de seu gráfico é desenhar uma linha horizontal, se for cortada na curva em mais de um ponto, a função não é injetiva.

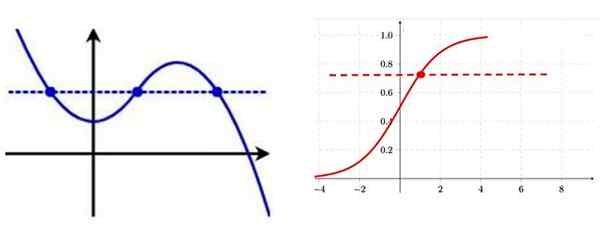À esquerda uma função injetiva, observe que existem vários pontos do gráfico com a mesma coordenada vertical. À direita, uma função injetiva, em cada um dos pontos da curva, ele tem uma coordenada "y" em particular. Fonte: f. Zapata.

V.2) função superjectiva

Nas funções onjetivas, Todos os elementos do conjunto de chegada são a imagem de algum elemento do conjunto inicial. Um exemplo de função excessiva é a mesma f (x) = 5x -2, mas g (x) = x² Não é, uma vez que os valores tomados g (x) são apenas os reais positivos e os 0.

No entanto, o domínio pode ser redefinido para que G (x) fosse superjetivo, se, por exemplo, ele mudar para todos os reais positivos mais 0. 

V.3) Função bijetiva

Finalmente, uma função que é injetiva e superjectiva é chamada Bijetivo. Exemplos de funções bijetivas são: a função relacionada, a função exponencial e a função logaritmo.

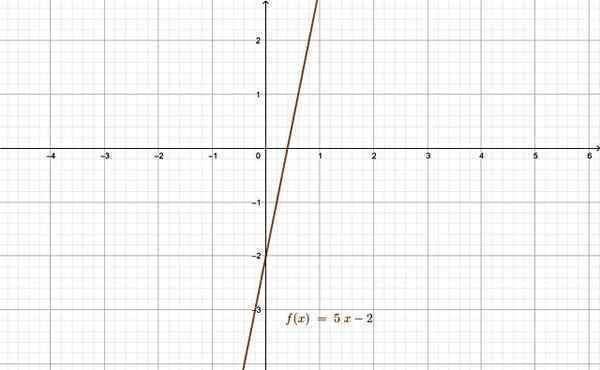A função relacionada é um bom exemplo de função bijectiva. Fonte: f. Zapata através da Geogebra.

Referências

1. Zona de matemática eletrônica. Tipos de funções. Recuperado de: emathzone.com.
2. Hoffman, J.G. Seleção de questões de matemática. Ed. Spphinx.
3. A matemática é divertida. Referência de funções do Commons. Recuperado de: Mathisfun.com.
4. Requena, b. Fórmulas do Universo. Tipos de funções. Recuperado de: universoformulas.com.
5. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.