Teorema verde, demonstração, aplicações e exercícios

Ele Teorema verde É um método de cálculo usado para relacionar integrais de linha com integrais de área dupla ou de superfície. As funções envolvidas devem ser indicadas como vetor e campos definidos na trajetória C.

Por exemplo, uma expressão de linha integral pode ser muito complicada de resolver; No entanto, ao implementar o teorema de Green, as integrais duplas se tornam bastante básicas. É sempre importante respeitar o sentido positivo da trajetória, isso se refere à direção das agulhas do relógio.

O teorema de Green é um caso particular do teorema de Stokes, onde a projeção da função vetorial é realizada no plano XY.

[TOC]

Definição

A expressão de Green do teorema de Green é a seguinte:

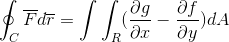
No primeiro termo, é observada a integral de linha definida pela trajetória "C", do escalar do produto entre a função do vetor "F" e o do vetor "R".

C: É a trajetória definida na qual a função vetorial será projetada desde que seja definida para esse plano.

F: função vetorial, onde cada um de seus componentes é definido por uma função como tal (f, g).

R: É uma tangente vetorial à região R na qual a integral é definida. Nesse caso, é operado com um diferencial deste vetor.

No segundo termo, vemos o teorema de Green desenvolvido, onde a dupla integral definida na região r da diferença de derivados parciais de g e f é observada, com relação a x e e e respectivamente. Para um diferencial de área que nada mais é do que o produto de ambos os diferenciais bilimensionais (DX.dy).

Este teorema é perfeitamente aplicável para integrais de espaço e superfície.

Demonstração

Para demonstrar o teorema de Green de uma maneira simples, essa tarefa será dividida em 2 partes. Primeiro, assumiremos que a função f vector tem apenas uma definição no versor Yo. Enquanto a função "G" correspondente ao versor J será igual a zero.

Pode atendê -lo: quantos centésimos se encaixam em um décimo? (Exemplos)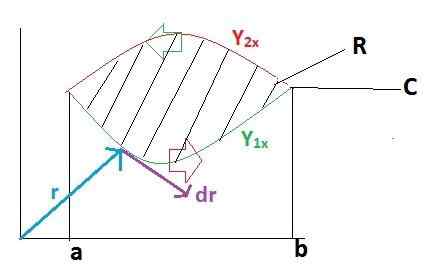Autor

F = f (x, y)Yo + G (x, y)J = f (x, y)Yo + 0

R = xYo + eJ

Dr = dxYo + DyJ

Primeiro, desenvolvemos a linha integral sobre a trajetória C, para a qual a trajetória foi setorizada em 2 seções que vão primeiro de A a B e depois de B a A.

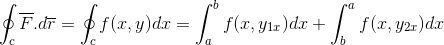
A definição do teorema fundamental do cálculo para uma integral definida é aplicada.

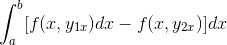
A expressão é reorganizada em uma única integral, é comum ao negativo e a ordem dos fatores é revertida.

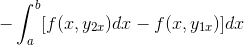
Ao observar em detalhes essa expressão, torna -se evidente que, ao aplicar os critérios de função primitiva, ela está na presença da integral da expressão derivada de f com relação a e. Avaliado em parâmetros

[e_1x , e_2x]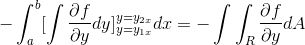

Agora basta assumir que a função de diversão do vetor é definida apenas para g (x, y)J. Onde, ao operar de uma maneira homologada para o caso anterior, é obtido:

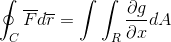
Finalmente, as duas demonstrações são feitas e se juntam no caso em que a função vetorial leva valores para ambos os versores. Dessa maneira, é mostrado como integral de linha após definir e ser considerado como uma trajetória unidimensional, ela pode ser totalmente desenvolvida para o avião e o espaço.

F = f (x, y)Yo + G (x, y)J

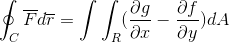
Dessa forma, o teorema de Green é demonstrado.

Formulários

As aplicações do teorema verde são amplas nos ramos da física e da matemática. Estes se estendem a qualquer aplicativo ou uso que possa ser dado para integração de linha.

O trabalho mecânico realizado por uma força f através de uma trajetória C pode ser desenvolvido por uma integral de linha que é expressa como uma dupla integral de uma área através do teorema de Green.

Pode servir a você: Prisma pentagonal: características, peças, vértices, bordas, volume

Os momentos de inércia de muitos corpos submetidos a forças externas em diferentes pontos de aplicação, também respondem a integrais desenvolvíveis com o teorema de Green.

Isso tem múltiplas funcionalidades nos estudos de resistência de materiais em uso. Onde valores externos podem ser quantificados e levados em consideração antes da elaboração de vários elementos.

Em geral, o teorema de Green facilita o entendimento e a definição de áreas em que as funções vetoriais são definidas em relação a uma região de acordo com uma trajetória.

História

Foi publicado em 1828 no trabalho Análise matemática para teorias de eletricidade e magnetismo, Escrito pelo matemático britânico George Green. Ele explora seções bastante decisivas na aplicação do cálculo na física, como o conceito de potencial, as funções do verde e as aplicações de seu teorema do automóvel intitulado.

George Green formalizou sua carreira estudantil aos 40 anos, até agora um ser matemático completamente auto -aprendido. Depois de estudar na Universidade de Cambridge, sua pesquisa continua, fazendo contribuições no campo da acústica, óptica e hidrodinâmica que ainda estão em vigor hoje.

Relacionamento com outros teoremas

O teorema de Green é um caso especial e surge de outros 2 teoremas muito importantes no ramo de cálculo. Estes são o teorema de Kelvin-Stokes e a divergência ou o teorema de Gausski.

Começando de qualquer um dos dois teoremas, você pode alcançar o teorema de Green. Certas definições e proposições são necessárias para desenvolver essas demonstrações.

Exercícios

- O exercício a seguir mostra como transformar uma linha integral em uma dupla integral em relação a uma região r.

A expressão original é a seguinte:

Pode atendê -lo: quanto vale x?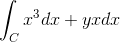

E deve ser avaliado na região triangular que se junta aos pontos (0, 0), (1, 0), (0, 1) denotado por c. Para este caso, o sentido positivo da virada será considerado.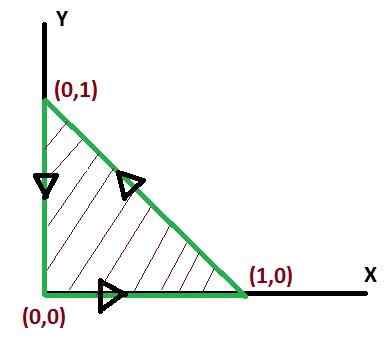

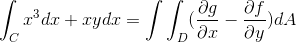
Onde as funções correspondentes a f e g são tiradas de

f (x, y) = x³                      g (x, y) = yx

df/dy = 0 dg/dx = y

É importante definir as funções que compõem os limites da região C, para poder montar o produto diferencial que cobrirá completamente a região.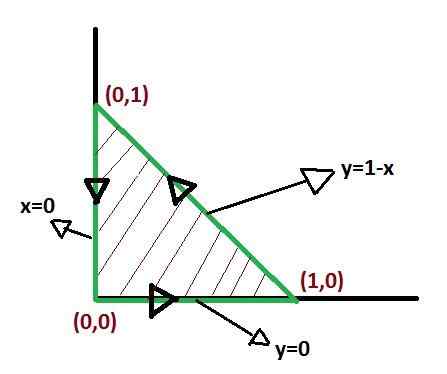

Não existe uma maneira única de definir limites de integração ao aplicar o teorema de Green. Mas existem formas em que as integrais após serem definidas podem ser mais simples. De tal maneira que a otimização dos limites de integração merece atenção.

Para este caso, essa expressão é considerada: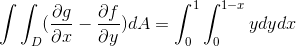

Onde, na solução das integrais, obtemos:

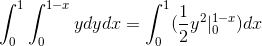
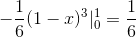
Este valor corresponde em unidades cúbicas à região abaixo da função vetorial e na região triangular definida por c.

No caso da linha integral sem executar o método verde, teria sido necessário parametrizar as funções em cada seção da região. Isto é, faça 3 integrais parametrizados para resolução. Esta é uma evidência suficiente da eficácia de que Robert Green contribuiu com seu teorema para o cálculo.

Referências

1. Introdução à Mecânica de Continuação. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23 de julho. 2009
2. Cálculo multivariável. James Stewart. Cengage Learning, 22 de março. 2011
3. Uma história informal do teorema de Green e idéias associadas. James Joseph Cross. Departamento de Matemática, Universidade de Melbourne, 1975
4. Comportamento de calor usando funções verdes. Kevin d. Cole, James V. Beck, a. Haji-Sheikh, Bahman Luckouhi. Taylor & Francis, 16 de julho. 2010
5. Aplicação do teorema de Green à extremidade de integrais lineares. Centro de Informações Técnicas de Defesa, 1961