Teorema da Euclid

O que é o teorema de Euclides?

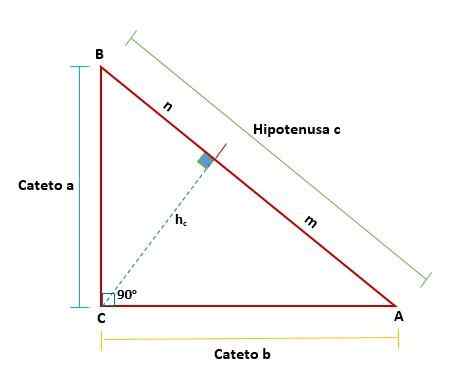
Ele Teorema da Euclid Ele demonstra as propriedades de um triângulo direito desenhando uma linha que a divide em dois novos retângulos que são semelhantes entre si e, por sua vez, são semelhantes ao triângulo original; Então, há uma relação de proporcionalidade.

Euclides foi um dos maiores matemáticos e geômetros da velhice que fez várias demonstrações de teoremas importantes. Um dos principais é o que leva seu nome, que teve uma ampla aplicação.

Isso ocorreu porque, através desse teorema, as relações geométricas existentes no triângulo retângulo explica, onde isso está relacionado às suas projeções na hipotenusa.

Fórmulas e demonstração

Teorema da Euclides propõe que em todos os triângulo direito, quando uma linha é desenhada - que representa na altura que corresponde ao vértice do ângulo reto em relação à hipotenusa - dois retângulos são formados a partir dos triângulos originais do original.

Esses triângulos serão semelhantes entre si e também serão semelhantes ao triângulo original, o que significa que seus lados semelhantes são proporcionais entre si:

Os ângulos dos três triângulos são congruentes; Isto é, quando girado a 180 graus em seu vértice, um ângulo coincide no outro. Isso implica que todos serão iguais.

Dessa maneira, você também pode verificar a semelhança que existe entre os três triângulos, para a igualdade de seus ângulos. Desde a similaridade dos triângulos, Euclides estabelece as proporções destes de dois teoremas:

• Teorema da altura.
• O teorema de Catetos.

Este teorema tem uma ampla aplicação. Nos tempos antigos, era usado para calcular alturas ou distâncias, representando um grande avanço para a trigonometria.

Pode atendê -lo: cálculo de abordagens usando diferenciais

Atualmente, é aplicado em várias áreas baseadas em matemática, como engenharia, física, química e astronomia, entre muitas outras áreas.

Teorema da altura

Este teorema estabelece que em qualquer triângulo retângulo, a altura desenhada do ângulo reto em relação à hipotenusa é a média proporcional geométrica (o quadrado da altura) entre as projeções dos cotetos que determina na hipotenusa.

Ou seja, o quadrado da altura será igual à multiplicação das pernas projetadas que formam a hipotenusa:

h_c² = m _* n

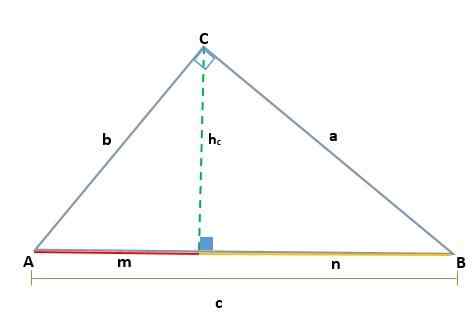
Demonstração

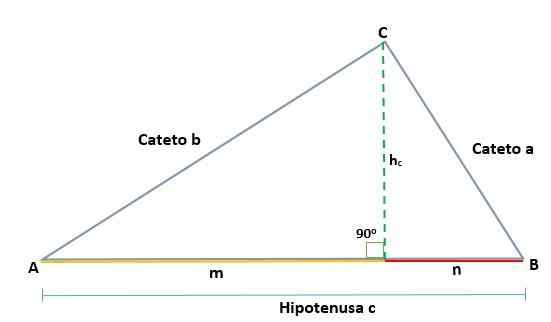
Dado um triângulo ABC, que é retângulo no vértice C, dois retângulos semelhantes, ADC e BCD são gerados; Portanto, seus lados correspondentes são proporcionais:

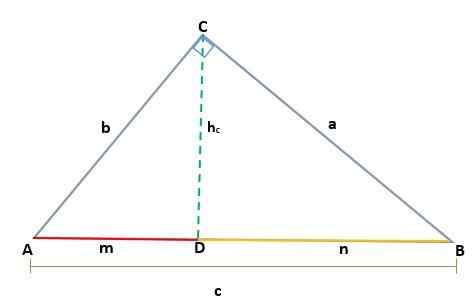
De tal maneira que a altura h_c Ele corresponde ao segmento de CD, corresponde à hipotenusa ab = c, então você precisa::

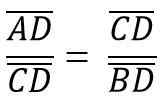
Por sua vez, isso corresponde a:

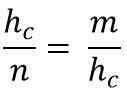
Limpar a hipotenusa (h_c), Para multiplicar os dois membros da igualdade, você precisa::

h_{C *} h_{C =} m _* n

h_c² = m _* n

Assim, o valor da hipotenusa é dado por:

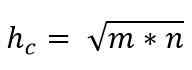
O teorema de Catetos

Este teorema estabelece que, em todo triângulo certo, a medida de cada cateto será a média proporcional geométrica (o quadrado de cada cateto) entre a medida da hipotenusa (completa) e a projeção de cada um nele:

b² = c _* m

para² = c_* n

Demonstração

Dado um triângulo ABC, que é retângulo no vértice C, de modo que sua hipotenusa é C, ao desenhar a altura (h) as projeções das categorias A e B são determinadas, que são os segmentos M e N, respectivamente, e que estão em A hipotenusa.

Assim, a altura desenhada no triângulo retângulo ABC gera dois retângulos semelhantes, ADC e BCD, para que os lados correspondentes sejam proporcionais, assim:

Pode servir a você: parabolóide hiperbólico: definição, propriedades e exemplos

Db = n, que é a projeção do CB Cateto na hipotenusa.

Ad = m, que é a projeção do CACETO AC na hipotenusa.

Então, a hipotenusa C é determinada pela soma das pernas de suas projeções:

C = m + n

Devido à semelhança dos triângulos ADC e BCD, você precisa::

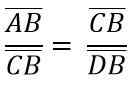
O acima é o mesmo que:

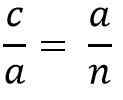
Limpando o "A" Cateto para multiplicar os dois membros da igualdade, você precisa::

para _* a = c _* n

para² = c _* n

Assim, o valor do Cateto "A" é dado por:

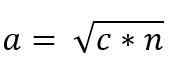
Da mesma forma, devido à semelhança dos triângulos ACB e ADC, você precisa::

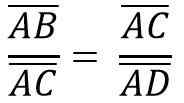
O acima é igual a:

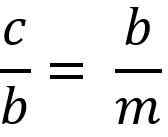
Limpando o Cateto "B" para multiplicar os dois membros da igualdade, você deve::

b _* b = c _* m

b² = c _* m

Assim, o valor do Cateto "B" é dado por:

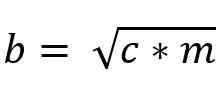
Relação entre teoremas de Euclides

Teoremas com referência à altura e as categorias estão relacionadas entre si, porque a medida de ambos é feita com relação à hipotenusa do triângulo retângulo.

Através da relação de teoremas de euclides, o valor da altura também pode ser encontrado; Isso é possível limpando os valores de M e N do teorema da categoria e são substituídos no teorema da altura. Dessa maneira, é cumprido que a altura é igual à multiplicação das pernas, dividida pela hipotenusa:

b² = c _* m

M = b² ÷ c

para² = c _* n

n = a² ÷ c

No teorema da altura, M e N são substituídos:

h_c² = m _* n

h_c² = (b² ÷ c) _* (para² ÷ c)

h_c = (b² _* para²) ÷ c

Exercícios resolvidos

Exemplo 1

Dado o triângulo ABC, retângulo em A, determine a medida de AC e AD, se AB = 30 cm e BD = 18 cm

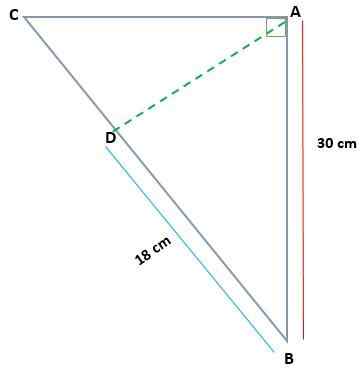
Solução

Nesse caso, existem as medidas de uma das pernas projetadas (BD) e uma das torques do triângulo original (AB). Dessa forma, você pode aplicar o teorema da categoria para encontrar o valor do BC Cateto.

Pode atendê -lo: regra de correspondência de uma função

Ab² = Bd _* Bc

(30)² = 18 _* Bc

900 = 18 _* Bc

BC = 900 ÷ 18

BC = 50 cm

O valor do CD Cateto pode ser encontrado sabendo que BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Agora é possível determinar o valor do CAC Cateto, aplicando novamente o teorema da categoria:

AC² = CD _* Bd

AC² = 32 _* cinquenta

AC² = 160

AC = √1600 = 40 cm

Para determinar o valor da altura (AD), o teorema da altura se aplica, uma vez que os valores das categorias projetadas CD e BD são conhecidas:

DE ANÚNCIOS² = 32 _* 18

DE ANÚNCIOS² = 576

Ad = √576

AD = 24 cm

Exemplo 2

Determine o valor da altura (h) de um triângulo MNL, retângulo em n, conhecendo as medidas dos segmentos:

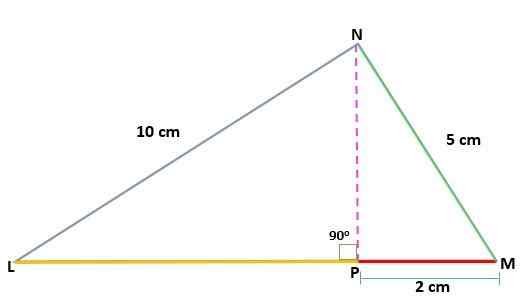
NL = 10 cm

Mn = 5 cm

Pm = 2 cm

Solução

Você tem a medida de uma das pernas projetadas na hipotenusa (PM), bem como as medidas das categorias originais do triângulo. Dessa forma, você pode aplicar o teorema da categoria para encontrar o valor do outro Cateto projetado (LN):

Nl² = Pm _* LM

(10)² = 5 _* LM

100 = 5 _* LM

Pl = 100 ÷ 5 = 20

Como o valor das categorias e a hipotenusa já é conhecida, através da relação dos teoremas da altura e das categorias, pode ser determinada o valor da altura:

Nl = 10

Mn = 5

LM = 20

H = (b² _* para²) ÷ c.

H = (10² _* 5²)  ÷ (vinte)

H = (100 _* 25) ÷ (vinte)

H = 2500 ÷ vinte

H = 125 cm.