Teorema de Bernoulli

Explicamos o que é o teorema, equações, aplicações, aplicações e resolver um exercício

Qual é o teorema de Bernoulli?

Ele Teorema de Bernoulli Ele afirma que, em um fluido ideal que circula em um conduíte, a energia mecânica por unidade de volume do fluido é constante em todas as seções do tubo, independentemente de que tenham diferentes seções transversais de área e altura.

Agora, um fluido ideal é aquele que não pode ser comprimido, portanto sua densidade é fixa, independentemente do valor da pressão.

Além disso, um fluido ideal tem viscosidade zero, ou seja, não há atrito entre as camadas de fluido e nem entre o fluido e as paredes do duto.

Condições de incompressibilidade e viscosidade nula são essenciais para aplicar o teorema de Bernoulli. Também é necessário que o fluxo seja estacionário, ou seja, o fluxo não varia com o tempo.

Por outro lado, o fluxo deve ser laminar, para que não haja redemoinhos ou turbulência durante a passagem do duto.

Equação de Bernoulli

A equação de Bernoulli tem três termos, o trabalho realizado pela imprensa P, energia cinética e energia potencial gravitacional para cada unidade de fluido de densidade volumétrica ρ

A equação de Bernoulli é:

Por outro lado, a equação de continuidade estabelece que em um fluido ideal o fluxo é constante em todas as seções do tubo de fluxo. Isto é, o volume de fluido na mesma unidade de tempo é o mesmo em todas as seções do tubo.

Se o fluxo for q, então:

Q = constante

Com:

Q = a · v

Onde a é a área de seção transversal do tubo e v é a velocidade do fluido.

Pode atendê -lo: satélites artificiais

Note -se que nas seções mais estreitas do tubo, o fluido deve circular mais rapidamente, pois permanece constante, embora varie. Portanto, a energia cinética por unidade de volume é maior.

Como o teorema de Bernoulli estabelece que a energia mecânica é constante em todas as seções, nas seções mais estreitas de maior energia cinética, a energia potencial diminui. 

A energia potencial consiste em energia gravitacional por unidade de volume mais o trabalho realizado pela pressão em um volume unitário, portanto, diminuindo a energia potencial também diminui a pressão.

Em resumo, o efeito combinado do princípio da continuidade e do teorema de Bernoulli resulta nas seções estreitas do tubo de fluxo, onde a velocidade do fluido é maior, a pressão cai em relação às seções mais amplas.

Termos na equação de Bernoulli

1) Trabalho realizado pela pressão por unidade de volume 

Em uma seção de seção transversal da área para, O fluido move uma quantidade s, Por causa da pressão p que produz uma força f = pulas.

O trabalho realizado pela força é:

F⋅ s = p⋅ a⋅ s

À medida que o produto A A progre.

2) energia cinética de um volume unitário de fluido

Como o fluido é incompressível, sua densidade tem um valor fixo chamado ρ.

Quando o fluido circula através de uma seção da seção transversal, movendo uma quantidade s em um tempo t, a taxa de fluxo é:

Pode servir a você: Segunda Lei da Termodinâmica: Fórmulas, Equações, Exemplos

v = s/t

E a energia cinética da referida parte do fluido é calculada por:

K = ½ ρ (a⋅s) V²

Mas se o volume deslocado (a⋅s) for unidade, o termo de energia cinética será dado por ½ ρ v².

3) energia potencial gravitacional de um volume unitário de fluido a uma altura h 

Para uma porção de fluido de massa m e altura h Em relação a um certo nível de referência, a energia gravitacional é dada por:

U = m⋅ g⋅ h

Se a massa m Corresponde a uma porção de fluido unitário, então a massa da porção corresponde à densidade ρ, Portanto, a energia potencial será ρ⋅ g⋅ h.

Aplicativos de Teorema de Bernoulli

Suporte aerodinâmico

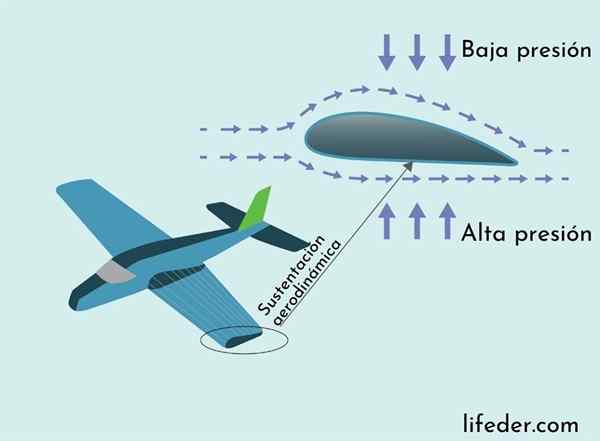O suporte aerodinâmico é explicado pelo teorema de Bernoulli

A força que impede um avião de vôo para colapso é a força de suporte aerodinâmica. A força de suporte líquida é direcionada verticalmente para cima e age ao longo da asa plana. Sua origem é explicada pelo teorema de Bernoulli.

A asa de um avião tem uma seção transversal com uma curva mais longa na parte superior e mais curta na parte inferior. Isso torna a rota aérea perto da superfície da asa na parte superior, então o ar flui mais rapidamente acima da asa do que a parte inferior. 

Como conseqüência do teorema de Bernoulli, a pressão do ar na parte superior da asa circulante é menor do que na parte inferior, resultando na força exercida pela diferença de pressão é direcionada para cima, apoiando o peso do plano, de acordo com ele pode ser visto na imagem a seguir.

Pode servir a você: Física durante os gregos (Antige Grécia)

Lançamento de bolas e bolas com efeito de curva

Em alguns esportes, como futebol, beisebol e cricke, jogadores experientes sabem como. É o que é chamado Lançamento de efeito.

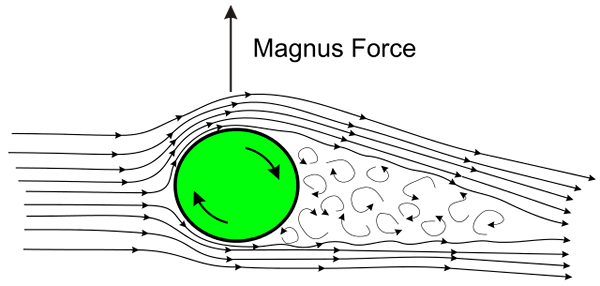Ilustração do efeito Magnus. Fonte: Wikimedia Commons

O efeito ocorre sempre que a bola ou a bola está girando rapidamente enquanto se move pelo ar. A rotação faz com que o ar até a superfície da bola seja arrastado por ela em duas direções opostas, uma a favor da direção da tradução e, do outro lado, contra a direção de deslocamento.

Como resultado do arrasto do ar, uma área de baixa pressão é produzida na face da bola e na face oposta em alta pressão, produzindo uma força líquida que desvia a trajetória natural da bola.

A explicação desse fenômeno conhecido como Efeito Magnus Reside precisamente no teorema de Bernoulli: onde o fluido circula rapidamente, a pressão é baixa e, do lado onde a pressão circula lenta.

Exercício resolvido

Um tubo horizontal tem uma seção de área A₁ = 40 centímetros quadrados e outra seção da seção de área A₂ quatro vezes mais baixo. Se o fluxo de água for 6 l/s, determine a diferença de pressão e a diferença de altura nos tubos verticais.

Solução 

A partir da equação de fluxo, cujo valor é q = 6 l/s:

Q = a · v

Você precisa então a velocidade na seção larga é de 1,5 m/se no trecho estreito 6 m/s.

Em seguida, aplicando e combinando a equação de Bernoulli no alongamento largo e estreito, é obtida uma diferença de pressão de 1700 pA, que corresponde a uma diferença de altura nos tubos verticais de 1,72 metros.