Regra de correspondência de uma função

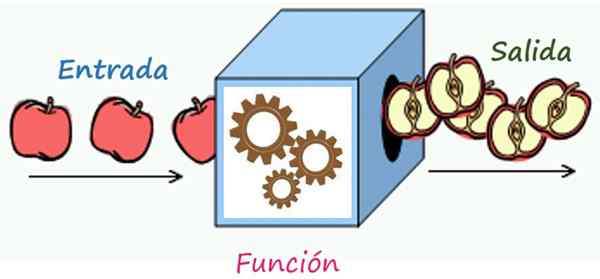A regra de correspondência é um mecanismo que transforma os elementos da entrada nos elementos de saída. Fonte: Wikimedia Commons/F. Zapata

Qual é a regra de correspondência de uma função?

O regra de correspondência de uma função Aponte a maneira como os elementos de um conjunto estão relacionados aos elementos de outro. Os elementos do primeiro conjunto são conhecidos como o domínio, e para os do segundo, como o Codomínio qualquer contradomínio.

A relação ou vínculo entre conjuntos pode ser especificada por instruções verbais ou escritas, no entanto, quando os conjuntos são numéricos, a regra de correspondência é indicada por uma fórmula.

Esta fórmula contém as operações que devem ser feitas com os elementos da montagem inicial e, assim, obter uma série de elementos incluídos no codomínio.

Agora, quando a relação entre os elementos é uma função, a regra de correspondência atende a duas condições especiais:

• Para cada um dos elementos do domínio está associado, através da regra de correspondência, um único elemento do codomínio, conhecido como o imagem.
• Esta imagem é única, em outras palavras, nenhum elemento do domínio está associado a mais de um elemento de codomínio.

Dessa forma, você pode imaginar a regra de correspondência de uma função como um mecanismo bloqueado em uma caixa. Cada valor de domínio, sem exceção, pode entrar na caixa e sair dela transformado, através das operações indicadas pela regra de correspondência. Os exemplos serão vistos imediatamente.

Exemplos

Exemplo 1

A regra de correspondência de uma função pode ser expressa como uma instrução por escrito, quando os elementos não são numéricos.

Por exemplo, há um conjunto de países, indicado como P, e outro conjunto de cidades C:

Pode atendê -lo: U -Test of Mann - Whitney: O que é e quando aplicado, execução, exemplo

P = Canadá, México, Espanha, EUA, França, Argentina, Brasil, Alemanha

C = Paris, Londres, Buenos Aires, Berlim, Cidade do México, Ottawa, Rio, Nova York, Madri, Washington, Berna, Roma, Brasília, Toronto

Ser a regra de correspondência F Entre p e c dado por:

F: P → c

Onde F É a regra "... cuja capital é .. ”, Que associa cada país em P (o conjunto inicial), com sua capital em C (o conjunto de chegada).

Por exemplo: “Espanha, cuja capital é Madri ". O elemento "Espanha" pertence ao conjunto p e o elemento "Madri" para todo o C, a chegada.

A representação desta função pode ser feita através de um diagrama de Venn ou simplesmente através de pares ordenados.

Os pares ordenados contêm, como o nome indica, dois elementos com uma ordem específica, neste exemplo, o primeiro elemento do par é o país e o segundo, sua capital.

Por sua vez, o diagrama de Venn é uma maneira de visualizar a função, mostrando os conjuntos de partida e chegada, bem como a regra de correspondência entre eles.

Representação de F como pares ordenados

F = (Canadá, Ottawa); (México, Cidade do México); (Espanha Madrid); (EUA; Washington); (França Paris); (Argentina Buenos Aires); (Brasil Brasília); (Alemanha, Berlim)

O primeiro par associa o Canadá, cuja capital é Ottawa, o segundo associado do México, cuja capital é Cidade do México e assim por diante.

Representação de F como um diagrama de Venn

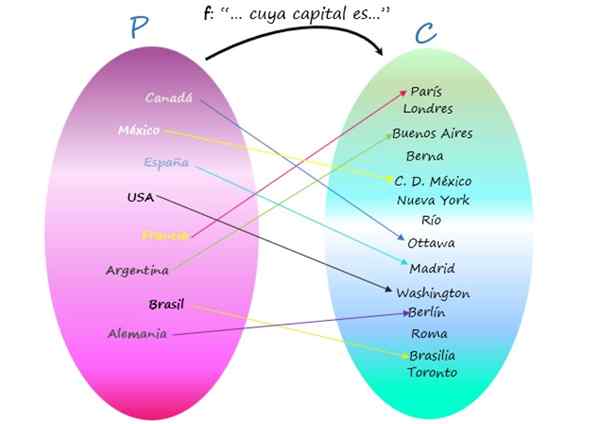
Observe que existem cidades que não são o capital de nenhum país, pois, embora sejam elementos do codomínio, eles não são uma imagem de nenhum elemento do conjunto inicial. Mesmo assim, o relacionamento é uma função, porque o importante é que cada país tem seu capital, e isso é único.

Pode servir a você: área de um pentágono regular e irregular: como é tomado, exercícios

O subconjunto formado pelos elementos do codomínio que são a imagem de algum elemento do domínio é chamado alcance ou função da função. Para o exemplo, a rota r de F é:

R = Paris, Buenos Aires, Cidade do México, Ottawa, Madri, Berlim, Washington, Brasília

Vale a pena perguntar se um relacionamento entre C e P pode ser estabelecido, onde C se torna o conjunto inicial e a chegada. A resposta é sim, mas não seria uma função, porque existem cidades que não são capitais, como Nova York, ou o país do qual eles são capital não aparece entre os elementos do complexo P, como a Roma.

Exemplo 2

Quando o conjunto de partida e o conjunto de chegada são numéricos, a regra de correspondência da função que os vincula é uma fórmula. Por exemplo, seja o domínio de uma função o seguinte conjunto:

D = 0, 1, 2, 3, 4, 5, 6)

A regra de correspondência F: D → R que vincula os elementos de D ao conjunto de números reais r é:

F: "Dobro"

Se "X" for um elemento do conjunto inicial, F (x) é o elemento correspondente do conjunto de chegada, e a regra de correspondência será escrita assim:

f (x) = 2x

Codomínio é o conjunto de números reais. Um subconjunto do reais é a rota desta função, o conjunto de números cujo valor é duas vezes mais como x:

R = 0, 2, 4, 6, 8, 10, 12

Na forma de pares ordenados, a regra de correspondência resulta em:

F = (0.0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Pares ordenados podem ser gráficos no avião cartesiano. O primeiro elemento do torque é colocado no eixo horizontal, também chamado de eixo dos abcissas ou eixo "X", enquanto o segundo passa no eixo vertical, eixo do eixo ordenado ou simplesmente "y":

Pode atendê -lo: propriedade distributiva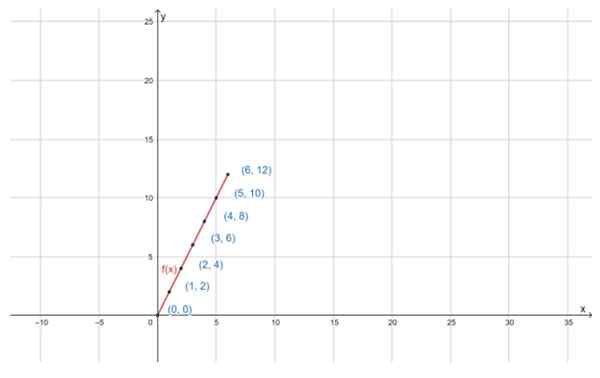 O gráfico da função f (x) = 2x, para o domínio d especificado, é uma linha reta. Fonte: f. Zapata através da Geogebra

Exercícios

Determine a regra de correspondência para os seguintes relacionamentos, indicando se são ou não funções. O conjunto de números naturais é n e o do real é r.

Indicam também o domínio, codomínio e a rota da função, nos casos em que corresponde:

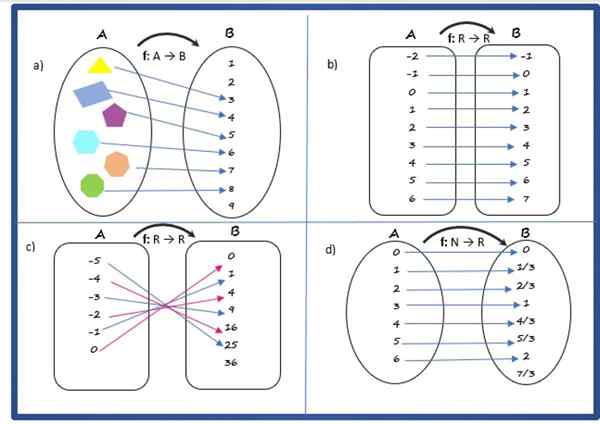
Solução para

É uma função, uma vez que cada elemento do conjunto inicial, consistindo em polígonos, tem uma imagem única no conjunto de chegada.

A regra de correspondência relaciona o polígono ao número de seus lados, o domínio consiste em conjunto de um dos polígonos:

A = Triangle, quadrilateral, Pentágono, hexágono, heptagon, octógono

Codomínio é o conjunto dos primeiros números naturais, incluindo 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

E os CO C são os números naturais de 3 a 8:

C = 3, 4, 5, 6, 7, 8

Solução b

É uma função, pois atende às condições especificadas acima.

A regra de correspondência é:

f (x) = x + 1

A regra de correspondência indica que a função é definida por R → R, portanto, o domínio é o conjunto de números reais. E o co -ominium e a rota também coincidem com o real.

Solução c

É uma função, com a regra de correspondência:

f (x) = x²

Domínio e codomínio são um conjunto de reais, mas a rota consiste apenas em números reais positivos, indicados como r⁺ e incluindo 0.

Solução d

É uma função. Sua regra de correspondência é:

f (x) = x/3

Seu domínio é o conjunto de números naturais n e codomínio, assim como a rota, são os n números n verdadeiros R.