Qual é a diretriz? (Geometria)

O diretivo Na geometria, consiste em uma curva, superfície ou volume que permanece fixo e determina a maneira como um objeto geométrico é formado. Por exemplo, por uma linha outras curvas, como superfícies cônicas e revolucionárias, como o cilindro circular reto são estabelecidas.

A curva de diretrizes também pode ser uma circunferência. Um cilindro circular reto pode ser formado deixando um raio ri -r rión ri.

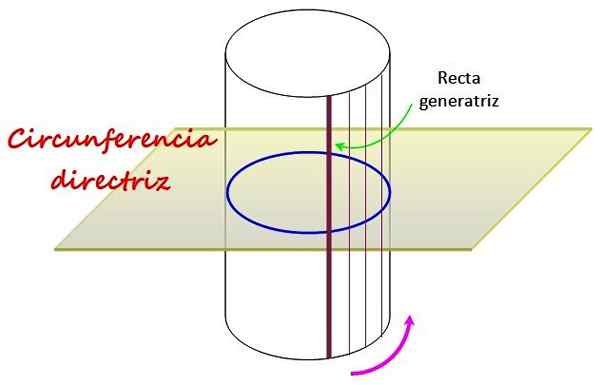
figura 1. Um cilindro circular reto tem como guia um círculo, em torno da qual uma linha reta chamada Geratrix se move. Fonte: f. Zapata.

A circunferência, que está no plano desenhada na figura, determina a forma da superfície curva do cilindro circular reto, que é gerado girando a linha ao redor, chamada Geratrix reto.

Se a curva de orientação não for uma circunferência, mas outra curva, outros tipos de cilindro são gerados, como o cilindro elíptico, cuja diretriz é uma elipse.

Uma circunferência também pode atuar como uma diretriz para gerar outra curva, esse é o caso do Epitrocóide, Uma curva no avião gerado por um ponto, que por sua vez está em um círculo menor que rola sem deslizar, ao redor da diretriz.

É mais fácil apreciá -lo visualmente pela seguinte animação:

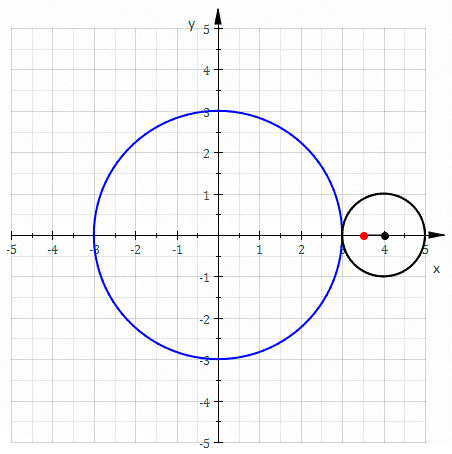Figura 2. A curva vermelha é chamada Epitrocídio e sua curva de diretrizes. Fonte: Wikimedia Commons. Sam Derbyshire na Wikipedia inglesa/CC BY-S (http: // criativecommons.Org/licenças/BY-SA/3.0/).

A curva de diretrizes em superfícies cilíndricas

As superfícies cilíndricas são classificadas de acordo com sua curva de diretrizes em cilindros:

-Circular

-Elíptico

-Parabólico

-Hiperbólico

Quando uma superfície cilíndrica tem uma diretriz que está em um plano perpendicular à da linha de generatrix, a equação da referida superfície é a mesma que a diretriz da diretriz.

Pode atendê -lo: qual é a relação entre a área de Rhombus e o retângulo?

Os cilindros pertencem ao grupo de Superfícies quadriciais, cuja equação é a segunda série com três variáveis. A forma geral é:

Machado² + Por² + Cz² + Dxy + exz + fyz + gx + hy + iz + k = 0

Onde coeficientes a, b, c ... são números reais.

Os cilindros são os corpos geométricos tridimensionais mais comuns e úteis que podem ser encontrados, especialmente os cilindros circulares retos, mas os outros tipos de cilindros descritos abaixo também têm aplicações em engenharia e design.

Cilindro circular reto

Sua diretriz é um círculo C que está em um plano perpendicular ao cilindro, como mostra a Figura 1, uma vez que a linha Geratrix, que é executada para C para formar a superfície lateral, é perpendicular a C.

A equação da circunferência C no plano XY, focado na origem (0,0) é:

x² + e² = R²

Onde r, o raio da circunferência obviamente será o raio do cilindro. A altura H do cilindro se estende ao longo do eixo z, perpendicular ao plano XY.

Cilindro elíptico

A diretriz é uma elipse no plano XY centrado na origem (0,0), cuja equação é:

A Geratrix é uma linha perpendicular ao plano XY, que se move ao redor da elipse para dar origem à superfície lateral. A elipse pode estar em qualquer altura z no avião XY.

Por exemplo, a equação elipse:

4x² + 9y² = 36

É a curva de diretrizes que dá origem ao cilindro elíptico cuja equação é 4x² + 9y² = 36, mais z = 0. Adicionando esta última expressão, fica claro que é a superfície.

Pode servir a você: Erro de amostragem: fórmulas e equações, cálculo, exemplos

Cilindro parabólico

Nesse caso, a diretriz é uma parábola, que pode ser da forma y = x². Assim, o cilindro é direcionado ao longo do eixo z e forma parábolas de empilhamento com um vértice em (0,0) ao longo desse eixo.

O cilindro parabólico tem aplicação na energia solar, já que alguns colecionadores têm espelhos dessa maneira, através da qual a luz solar está concentrada no foco. Este ponto passa um tubo reto dentro do qual um óleo atinge temperaturas até 400 º C.

Cilindro hiperbólico

No cilindro hiperbólico, a equação da diretriz é a hipérbole centrada na origem:

O cilindro é formado na pilha.

Superfície da revolução

A curva de diretrizes de uma superfície de revolução é o mesmo eixo da revolução, a linha em torno da qual a curva responsável por gerar a superfície.

A curva que gira pode ter forma arbitrária, dessa maneira uma área é gerada como visto nesta animação:

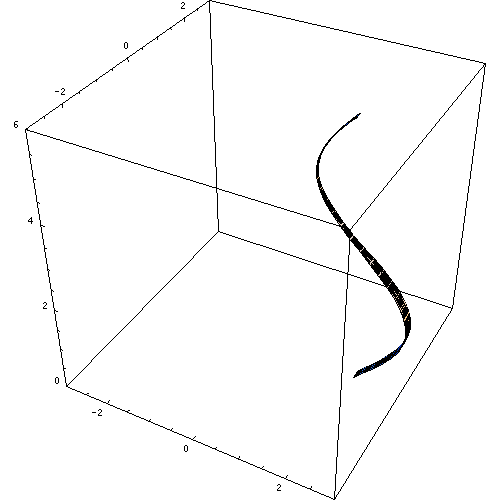Figura 3. Uma superfície de revolução. Fonte: Wikimedia Commons. https: // upload.Wikimedia.Org/wikipedia/commons/e/e7/rotaçõeskoerper_animation.Gif.

Se outra linha for virada na diretriz, o já familiar cilindro circular reto é obtido. Da mesma maneira, outras superfícies de revolução podem ser obtidas, como superfícies cônicas, esféricas e toroidais de revolução.

Superfície cônica

Uma superfície cônica é gerada pelo movimento de uma linha Geratrix que sempre passa pela curva plana fixa ou curva de diretrizes e pelo ponto fixo chamado vértice, que não pertence ao plano de diretrizes.

Pode servir a você: esperança matemática: fórmula, propriedades, exemplos, exercícios

O vértice ou a ponta divide o cone em duas partes, chamado folhas qualquer galhos.

Exercícios resolvidos

- Exercício 1

Encontre a área lateral do cilindro circular alto da altura 25 cm, cuja curva de diretrizes é a circunferência do raio de 6 cm, focada na origem.

Solução

A área lateral do cilindro é o produto da duração da diretriz por altura. Se r é o raio da circunferência e H é a altura do cilindro, a área é dada por:

A = 2πr x h = 2πx 6 cm x 25 cm = 942.5 cm²

- Exercício 2

Você tem a seguinte equação que corresponde a uma superfície quadricular:

x² + e² + 2z² +2xz - 2yz = 1

Indicar que superfície é e qual é a equação da diretriz.

Solução

Fazendo z = k, onde k é constante, é obtido:

x² + e² + 2k² +2kx - 2ky = 1

Reorganizamos os termos da seguinte forma:

(x² + 2kx) + (e²- 2ky) = 1-2k²

Quadrados devem², Para não alterar nenhum dos parênteses:

(x² + 2kx + k² - k² ) + (e² - 2ky + k² - k²) = 1-2k²

(x² + 2kx + k²) - k²  + (e²- 2ky + k²) - k² = 1-2k²

Dessa forma, permanece:

(x + k)² + (e que)² = 1

Assim como a equação de um círculo central (-k, k) e o raio 1, a superfície é um cilindro circular reto, também da Rádio 1, desde que a linha Geratrix seja perpendicular à referida circunferência.

Por exemplo, fazendo k = 0, a equação é reduzida à circunferência centrada na origem (0,0) cujo raio é 1:

x² + e² = 1

Referências

1. Gaussianos. Representam superfícies tridimensionais. Recuperado de: gaussianos.com.
2. Kindle, j. Teoria e problemas de geometria analítica. McGraw Hill. Série Schaum.
3. Superfícies como locais geométricos. Recuperado de: álgebra.FRLP.Utn.Edu.ar.
4. Suárez, m. Superfícies. Recuperado de: assuntos.Unq.Edu.ar.
5. Superfícies quadriciais. Recuperado de: sistemas.fciencias.Unam.mx.