Produtos notáveis

O que são produtos notáveis?

Produtos notáveis ​​são operações algébricas, onde são expressas multiplicações de polinômios, que não precisam ser tradicionalmente resolvidas, mas com a ajuda de certas regras, os resultados do mesmo podem ser encontrados.

Os polinômios são multiplicados se, portanto, é possível que eles tenham muitos termos e variáveis. Para impedir o processo, as regras dos produtos notáveis ​​são usados, que permitem multiplicações sem precisar ir a termo para termo.

Produtos e exemplos notáveis

Cada produto notável é uma fórmula que resulta de uma fatorização, composta por polinômios de vários termos, como binômios ou trinômios, chamados fatores.

Os fatores são a base de um poder e têm um expoente. Quando os fatores se multiplicam, os expoentes devem ser adicionados.

Existem várias fórmulas notáveis ​​de produtos, algumas são mais usadas do que outras, dependendo dos polinômios, e são os seguintes:

Binômio quadrado

É a multiplicação de um binomial por si só, expresso na forma de poder, onde os termos são adicionados ou subtraídos:

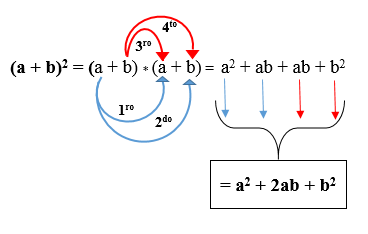
para. Binomial quadrado de soma: É igual ao quadrado do primeiro termo, além do dobro do produto dos termos, mais o quadrado do segundo termo. É expresso o seguinte:

(A + b)² = (a + b) _* (A + b).

Na figura a seguir, você pode ver como o produto é desenvolvido de acordo com a regra mencionada acima. O resultado é chamado de trinomial de um quadrado perfeito.

Exemplo 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Exemplo 2

(4a + 2b) = (4a)² + 2 (4º _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8AB) + 4b²

(4a + 2b) = 8a² + 16 ab + 4b².

b. Binomial de uma subtração quadrada: A mesma regra do binomial de uma soma é aplicada, apenas que neste caso o segundo termo é negativo. Sua fórmula é a seguinte:

(A - B)² = [(a) + (- b)]²

Pode atendê -lo: analogias numéricas: tipos, aplicações e exercícios

(A - B)² = a² +2º _* (-b) + (-b)²

(A - B)²   = a² - 2AB + b².

Exemplo 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Produto conjugado de binômios

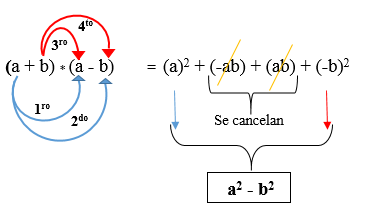
Dois binômios são conjugados quando os segundos termos de cada um são de sinais diferentes, ou seja, o do primeiro é positivo e o do segundo negativo ou vice -versa. É resolvido levantando cada quadrado monomial e subtraído. Sua fórmula é a seguinte:

(A + b) _* (A - B)

Na figura seguinte, o produto de dois binômios conjugados é desenvolvido, onde é observado que o resultado é uma diferença de quadrados.

Exemplo 1

(2a + 3b) (2a - 3b) = 4a² + (-6ab) + (6 ab) + (-9b²)

(2a + 3b) (2a - 3b) = 4a² - 9b².

Produto de dois binômios com um termo comum

É um dos produtos notáveis ​​mais complexos e pouco usados, porque é uma multiplicação de dois binômios que têm um termo comum. A regra indica o seguinte:

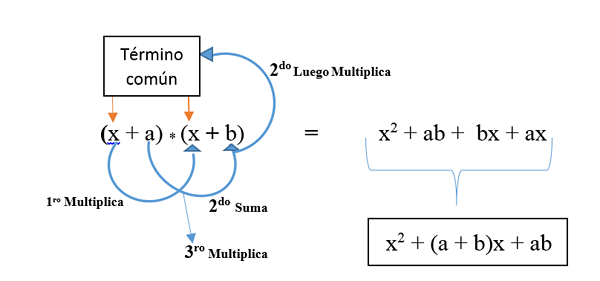
• O quadrado do termo comum.
• Além da soma dos termos que não são comuns e depois multiplique pelo termo comum.
• Além da soma da multiplicação dos termos que não são comuns.

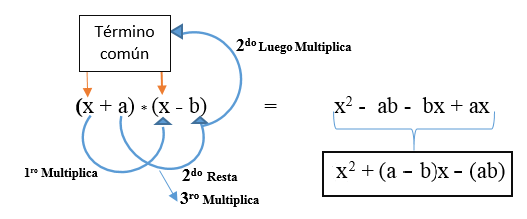
Está representado na fórmula: (x + a) _* (x + b) e é desenvolvido como mostrado na imagem. O resultado é um trinômio quadrado não perfeito.

Exemplo 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

Existe a possibilidade de que o segundo termo (o termo diferente) seja negativo e sua fórmula seja a seguinte: (x + a) _* (X - B).

Exemplo 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Também pode ser o caso de que ambos os termos diferentes sejam negativos. Sua fórmula será: (x - a) _* (X - B).

Pode servir você: Teorema Lamy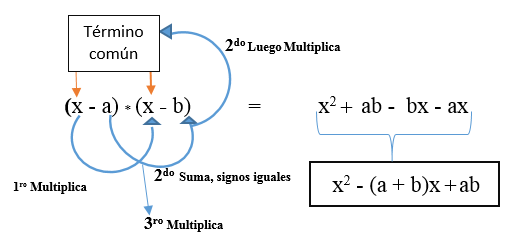

Exemplo 3

(3b - 6) _* (3b - 5) = (3b _* 3b) + (-6 - 5)_* (3b) + (-6 _* -5)

(3b - 6) _* (3b - 5) = 9b² + (-onze) _* (3b) + (30)

(3b - 6) _* (3b - 5) = 9b² - 33b + 30.

Polinomial quadrado

Nesse caso, existem mais de dois termos e, para desenvolvê -lo, cada um é cortado e adicionado junto com o dobro da multiplicação de um termo com outro; Sua fórmula é: (a + b + c)² E o resultado da operação é um trinomial quadrado.

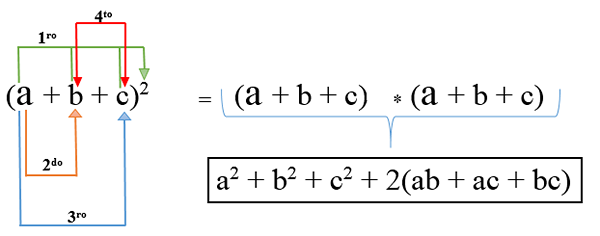
Exemplo 1

(3x + 2y + 4z)² = (3x)² + (2 e)² + (4z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4y² + 16z² + 12xy + 24xz + 16yz.

Binômio de cubo

É um produto notável complexo. Para desenvolvê -lo, o binomial é multiplicado por seu quadrado, como segue:

para. Para binomial para o cubo de uma soma:

• O primeiro termo cubo, mais o triplo do quadrado do primeiro termo pelo segundo.
• Mais triplicar o primeiro termo, no segundo quadrado.
• Mais o cubo do segundo termo.

(A + b)³ = (a + b) _* (A + b)²

(A + b)³ = (a + b) _* (para² + 2AB + b²)

(A + b)³ = a³ + 2º²B + ab² + BA² + 2AB² + b³

(A + b)³ = a³ + 3º²B + 3AB² + b³.

Exemplo 1

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = a³ + 9 a² + 27a + 27.

b. Para o binomial para o cubo de uma subtração:

• O cubo do primeiro termo, exceto o triplo do quadrado do primeiro termo pelo segundo.
• Mais triplicar o primeiro termo, no segundo quadrado.
• Menos o cubo do segundo termo.

(A - B)³ = (a - b) _* (A - B)²

(A - B)³ = (a - b) _* (para² - 2AB + b²)

(A - B)³ = a³ - 2º²B + ab² - BA² + 2AB² - b³

(A - B)³ = para³ - 3º²B + 3AB² - b³.

Exemplo 2

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Pode atendê -lo: dados não agrupados: exemplos e exercícios resolvidos

(B - 5)³ = b³ - 15b² +75b - 125.

Cubo trinomial

Desenvolve multiplicando -o por seu quadrado. É um produto notável muito extenso, porque há 3 termos levantados no cubo, além do triplo de cada termo crítico, multiplicado por cada um dos termos, além de seis vezes o produto dos três termos. Visto de uma forma melhor:

(A + B + C)³ = (A + b + c) _* (A + B + C)²

(A + B + C)³ = (A + b + c) _* (para² + b² + c² + 2AB + 2AC + 2BC)

(A + B + C)³ = A³ + b³ + c³ + 3º²B + 3AB² + 3º²C + 3ac² + 3b²C + 3bc² + 6ABC.

Exemplo 1

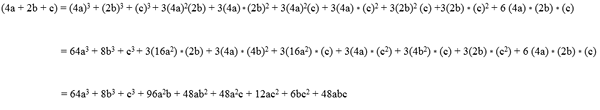
Exercícios resolvidos de produtos notáveis

Exercício 1

Desenvolva o seguinte binomial para o cubo: (4x - 6)³.

Solução

Lembrando que um binomial para o cubo é igual ao primeiro termo elevado ao cubo, exceto o triplo do quadrado do primeiro termo pelo segundo; mais triplicar o primeiro termo, no segundo quadrado, exceto o cubo do segundo termo.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288x² + 432X - 36.

Exercício 2

Desenvolva o seguinte binomial: (x + 3) (x + 8).

Solução

Você tem um binomial onde há um termo comum, que é x e o segundo termo é positivo. Para desenvolvê -lo, apenas o termo comum deve ser aumentado, mais a soma dos termos que não são comuns (3 e 8) e depois multiplique -os pelo termo comum, mais a soma da multiplicação dos termos que não são comuns.

(x + 3) (x + 8) = x² + (3 + 8) x + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Referências

1. Anjo, a. R. (2007). Álgebra Elementar. Pearson Education,.
2. Arthur Goodman, L. H. ( mil novecentos e noventa e seis). Álgebra e trigonometria com geometria analítica. Pearson Education.
3. Das, s. (s.F.). Matemática mais 8. Reino Unido: Sagar Ratna.
4. Jerome e. Kaufmann, k. eu. (2011). Álgebra elementar e intermediária: uma abordagem combinada. Flórida: Cengage Learning.
5. Pérez, c. D. (2010). Pearson Education.