Características do prisma pentagonal, peças, vértices, bordas, volume

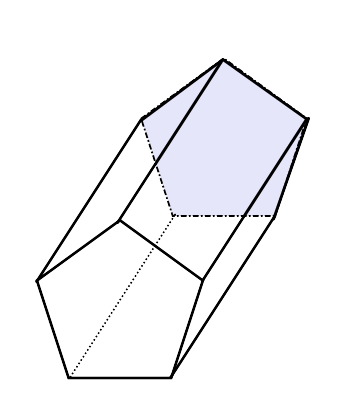
A Prism pentagonal É uma figura geométrica tridimensional cujas bases, idênticas, têm uma forma de Pentágono e também têm um total de 5 fintes na forma de paralelogramo.

Se os rostos são retangulares, diz -se que é um Prisma pentagonal direta, Enquanto se as bordas estiverem inclinadas para as bases, então é um prisma pentagonal oblíqua. Na imagem a seguir, há um exemplo de cada.

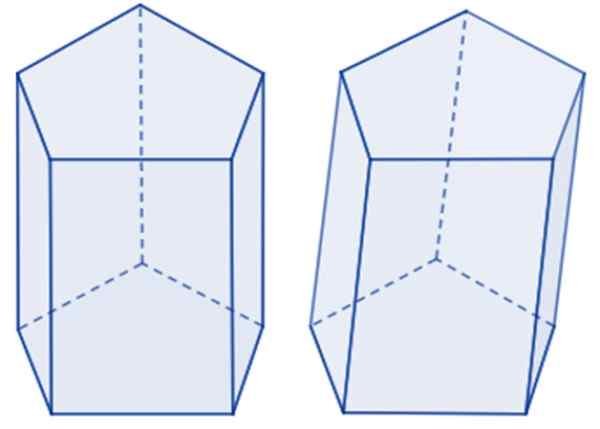Prisma pentagonal para a esquerda e oblíqua para a direita. Fonte: Wikimedia Commons.

O Pentágono base pode ser regular se seus cinco lados tiverem a mesma medida, assim como os ângulos internos, caso contrário, é um pentágono irregular. Se a base do prisma é regular, é sobre prisma pentagonal regular. Caso contrário, é um prisma pentagonal irregular.

Base irregular Prisms pentagonais usados ​​na construção moderna. Fonte: Flare de papel de parede.

Prisma pentagonal é uma estrutura harmoniosa que é usada na arquitetura e design de objetos, como o edifício moderno mostrado na figura superior. As janelas em forma de pentágono irregulares formam a base dos prismas.

[TOC]

Características do prisma pentagonal

-É uma figura geométrica tridimensional, as superfícies que o compõem contêm um certo volume.

-Suas bases são pentagons e seus rostos laterais podem ser retângulos ou paralelogramas.

-Tem vértices -os cantos das bordas prisma e bordas -bordas ou margens-.

-Se as bordas que unem as bases são perpendiculares a elas, o prisma é reto e, se forem inclinadas, o prisma é oblíquo.

-Quando a base é um pentágono cujos ângulos internos são menores de 180º, o prisma é convexo, Mas se um ou mais ângulos internos são maiores que 180º, é um prisma côncavo.

Elementos do prisma pentagonal

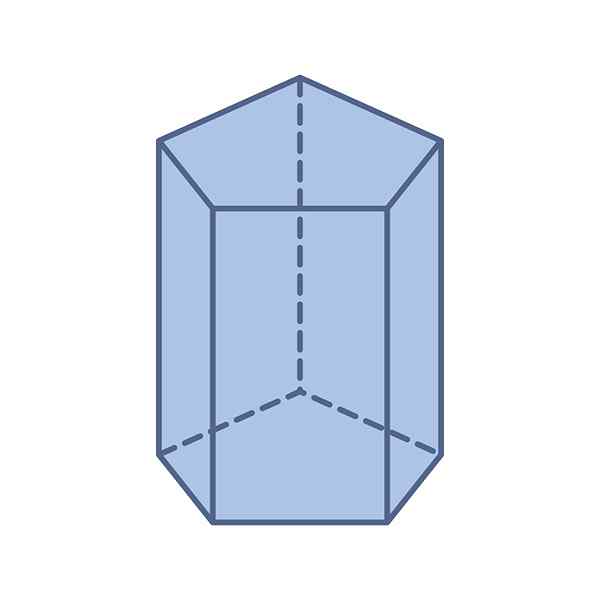
-Bases: Tem duas bases pentagonais e congruentes -suas medições são as mesmas -regulares ou irregulares.

Pode servir a você: Fórmula Geral: Equações Quadráticas, Exemplos, Exercícios

-Rostos: Um prisma pentagonal tem um total de 7 faces: as duas bases pentagonais e os cinco paralelogramas que compõem as laterais.

-Borda: segmento que se junta a duas bases, mostradas em vermelho na Figura 3 ou aquele que se junta a dois lados.

-Altura: Distância entre os rostos. Se o prisma for reto, essa distância coincide com o tamanho da borda.

-Vértice: ponto comum entre uma base e dois lados lados.

A figura inferior mostra um prisma pentagonal de base regular, no qual os segmentos que formam a base têm igual medida, chamados para.

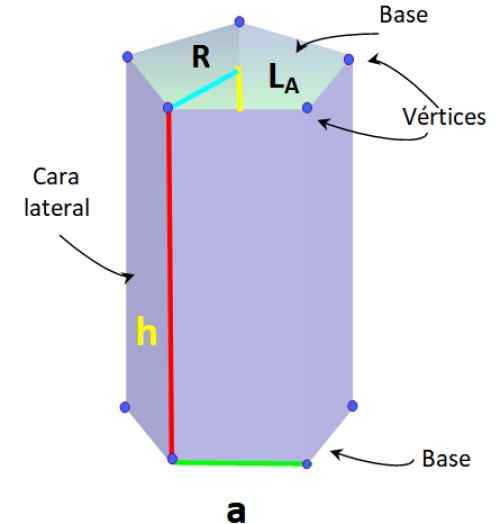 Elementos de prisma pentagonal regulares. Fonte: f. Zapata.

Esse tipo de prisma também possui os seguintes elementos, típicos do Pentágono regular:

-Rádio r: Distância entre o centro do Pentágono e um dos vértices.

-Apothem l_PARA: segmento que se junta ao centro com o ponto médio de um dos lados do Pentágono.

Quantos vértices um prisma pentagonal tem?

Em um Pentágono, existem 5 vértices e, como o prisma pentagonal tem dois pentágonos como bases, esse corpo tem um total de 10 vértices.

Quantas bordas um prisma pentagonal tem?

Você pode calcular o número de arestas para corpos geométricos com faces planas, como prismas, usando o Teorema de Euler Para poliedros convexos. Leonhard Euler (1707-1783) é um dos maiores matemáticos e físicos da história.

O teorema estabelece uma relação entre o número de faces, que chamaremos de C, a quantidade de vértices V e o total de arestas a da seguinte forma:

C+V = A+2

Para o prisma pentagonal que temos: c = 7 e v = 10. Limpeza para, o número de arestas:

Pode servir a você: Função Bijectiva: O que é, como é feito, exemplos, exercícios

A = C+V-2

Substituindo valores:

A = 7 + 10 - 2 = 15

Um prisma pentagonal tem 15 arestas.

Como obter o volume de um prisma pentagonal?

O volume do prisma pentagonal mede o espaço bloqueado pelos lados e as bases. É uma quantidade positiva que é calculada pela seguinte propriedade:

Qualquer plano que corta para o prisma perpendicularmente às suas bordas gera uma interseção da mesma maneira que a base, ou seja, um pentágono das mesmas dimensões.

Portanto, o volume do prisma pentagonal é o produto da área base e a altura do prisma.

Ser PARA_B a área base pentagonal e h A altura do prisma, então o volume V é:

V = a_B x h

Esta fórmula é geral, sendo válida para qualquer prisma, regular ou irregular, reto ou oblíquo.

O volume de um prisma sempre vem em unidades de comprimento alto ao cubo. Se o comprimento dos lados e a altura do prisma são apresentados em metros, o volume será expresso em m³, que "metros cúbicos" são lidos. Outras unidades incluem CM³, km³, polegadas³ e mais.

- Volume regular de prisma pentagonal

No prisma pentagonal regular, as bases são pentágions regulares, o que significa que o lado e os ângulos internos são os mesmos. Dada a simetria do corpo, a área do Pentágono e, portanto, o volume é facilmente calculado de várias maneiras:

Conhecendo a altura e a medição do lado

Ser para A medida do lado da base pentagonal. Nesse caso, a área é calculada por:

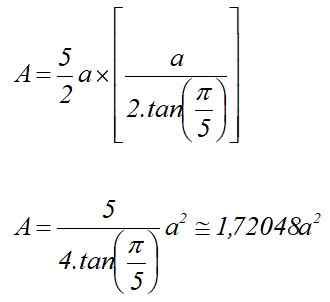
Portanto, o volume do prisma pentagonal regular da altura h é:

Pode atendê -lo: números imaginários: propriedades, aplicações, exemplos

V = 1.72048 a²⋅ h

Conhecendo a altura e a medida do rádio

Quando o Rádio r Da base pentagonal, essa outra equação pode ser usada para a área base:

A = (5/2) r²⋅ sen 72º

Dessa maneira, o volume do prisma pentagonal é dado por:

V = (5/2) r² ⋅ h ⋅ sen 72º

Onde h É a altura do prisma

Conhecendo a altura, medida de apoteme e valor do perímetro

A área base pentagonal pode ser calculada se seu perímetro p for conhecido, que é simplesmente a soma dos lados, bem como a medida do apothem l l l l l l l l l l l l l l l l l_PARA:

A = p. eu_PARA / 2

Multiplicando essa expressão pelo valor da altura h, Temos o volume do prisma:

V = P. eu_PARA .H / 2

- Volume irregular de prisma pentagonal

A fórmula dada no início é válida quando a base do prisma é um pentágono irregular:

V = a_B x h

Para calcular a área base, vários métodos são usados, por exemplo:

-Método de triangulação, que consiste em dividir o Pentágono em triângulos e quadriláteros, cujas respectivas áreas são facilmente calculadas. A área do Pentágono será a soma das áreas dessas figuras mais simples.

-Método dos determinantes de Gauss, para o qual você precisa conhecer os vértices da figura.

Uma vez que o valor da área é determinado, ela é multiplicada pela altura do prisma para obter o volume.

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Math Open Reference. Área de Polígono. Recuperado de: MathpenRef.com.
3. Fórmulas do Universo. Teorema de Euler para poliedros. Recuperado de: universoformulas.com.
4. Fórmulas do Universo. Área de um pentágono comum. Recuperado de: universoformulas.com.
5. Wikipedia. Prisma. Recuperado de: é.Wikipedia.com.
6. Wikipedia. Prism pentagonal. Recuperado de: é.Wikipedia.com.