Propriedades regulares de polígonos, elementos, ângulos, exemplos

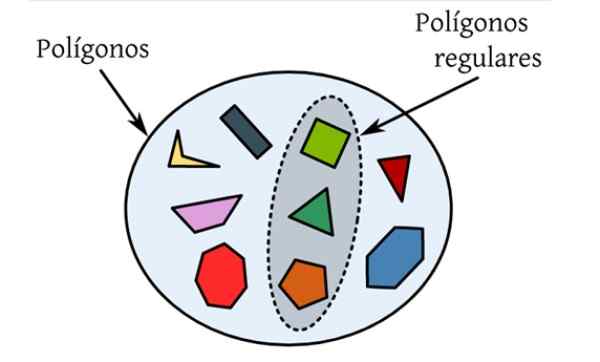
O Polígonos regulares Eles são aqueles que têm todos os seus lados e seus iguais ângulos internos. Na figura seguinte, há um conjunto de polígonos diferentes, que são figuras planas limitadas por uma curva fechada e somente aquelas que são destacadas atendem às condições a serem regulares.

Por exemplo, o triângulo equilátero é um polígono regular, uma vez que seus três lados medem o mesmo, assim como seus ângulos internos, que valem 60 º cada.

figura 1. Polígonos regulares são aqueles cujos lados e ângulos internos são os mesmos, como o triângulo equilátero e o quadrado. Fonte: Wikimedia Commons.

O quadrado é um quadrilateral com quatro lados de igual medida e cujos ângulos internos são 90º. É seguido pelo Pentágono comum, com cinco lados de tamanho igual e cinco ângulos internos de 108º cada.

Quando um polígono é regular, essa palavra é adicionada ao seu nome especial, portanto temos o hexágono comum, o heptagon comum e assim por diante.

[TOC]

Propriedades de polígonos regulares

As propriedades mais importantes dos polígonos regulares podem ser resumidas da seguinte forma:

-Os lados medem o mesmo, portanto são Equilaterais.

-São Equiagular, Bem, todos os seus ângulos internos têm igual medida.

-Eles sempre podem se registrar em uma circunferência, o que significa que eles se encaixam perfeitamente em um, o que é chamado circunferência circunscrita.

-Para um polígono regular de N lados, a medida de um ângulo interno α é:

α = [180 (n-2)]/n

-Diagonais n-3)/2 podem ser extraídos dos vértices de um polígono, seja regular ou não.

-A soma de ângulos externos É igual a 360º.

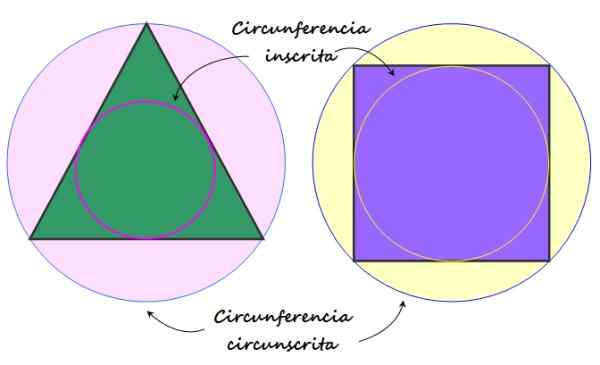Figura 2. Circunferência registrada e circunferência circunscrita para polígono regular. Fonte: f. Zapata.

Elementos de um polígono comum

Depois, apresentamos os principais elementos de um polígono comum, visualizado na figura inferior.

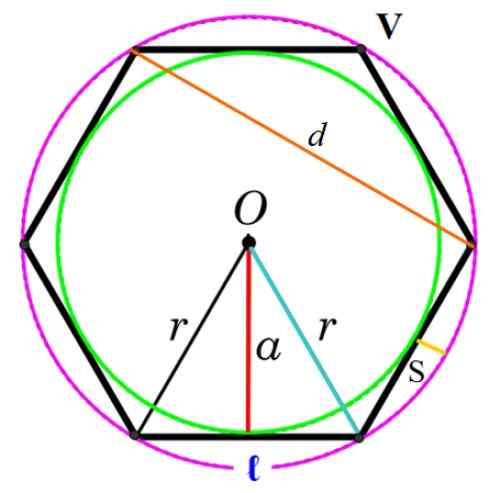Figura 3. Elementos do polígono comum. Fonte: f. Zapata.

Vértice

Ponto comum que tem dois lados consecutivos, indicados como V na figura.

Lado

É o segmento que se junta a dois vértices consecutivos do polígono e é indicado como ℓ ou l.

Diagonal

Segmento que se junta a dois vértices não consecutivos do polígono, na figura que é denotada como d.

Centro

É o centro comum da circunferência registrada e a circunferência circunscrita, indicada pela carta ou. Também pode ser visto como o único ponto que a equidista de ambos os vértices e os pontos médios de cada lado.

Rádio

É o rádio r da circunferência circunscrita e coincide com a distância entre O e um vértice.

Pode servir a você: axiomas de probabilidade: tipos, explicação, exemplos, exercícios

Apótema

Se denomina apótema ao raio da circunferência inscrito no polígono, representado na figura com uma letra para. O apothem é perpendicular ao lado e une isso com o centro O (segmento vermelho na Figura 3).

Conhecendo o raio r e o comprimento do lado, o apotem é calculado por:

Como, com efeito, o apotem é uma das categorias de um triângulo retângulo (veja a Figura 3), o outro Cateto sendo o valor de ℓ/2 (metade de um lado) e a hipotenusa do rádio r do polígono.

Quando o teorema de Pitágoras é aplicado ao referido triângulo, esta equação é obtida, o que é válido não apenas para o hexagon, mas para qualquer polígono regular.

Ângulo central

É o ângulo cujo vértice coincide com o centro ou cujos lados são os segmentos que unem o centro com dois vértices consecutivos. Sua medida em graus sexagesimal é 360º/n, onde n É o número de lados do polígono.

Sagita

É a diferença entre o raio do polígono e o apotem (veja a Figura 3). Denotando sagita como s:

S = r - a

Perímetro e área

Perímetro

É facilmente calculado adicionando os comprimentos dos lados. Como qualquer lado tem o mesmo comprimento L e existem n lados, o perímetro P é expresso como:

P = n.eu

Área

Em um polígono regular, a área A é dada pelo produto entre o semi-perímetro (metade do perímetro) e o comprimento do apoteme para.

A = p.A /2

Como o perímetro depende do número de lados n, acontece que:

A = (nl).A /2

Dois polígonos regulares podem ter o mesmo perímetro, mesmo que não tenham o mesmo número de lados, pois dependeria do comprimento dos lados.

No livro V do seu Coleção, O Pappus matemático de Alexandria (290-350), o último dos grandes matemáticos gregos da antiguidade, mostrou que, entre todos os polígonos regulares com o mesmo perímetro, aquele com a maior área é a com o maior número de lados.

Ângulos

A Figura 4 mostra os ângulos relevantes em um polígono regular, indicado com as letras gregas α, β e γ.

Ângulo central

Anteriormente, mencionamos o ângulo central, entre os elementos do polígono comum, é o ângulo cujo vértice está no centro do polígono e os lados são os segmentos que unem o centro com dois vértices consecutivos.

Para calcular a medida do ângulo central α, 360º é dividido por n, o número de lados. Ou 2π radianos entre n:

Pode atendê -lo: função injetiva: o que é consiste, para que é e exemplos

α = 360º/n

Equivalente em radianos para:

α = 2π /n

Ângulo interno ou ângulo interno

Na Figura 4, o ângulo interno β é aquele cujo vértice coincide com uma das figura e seus lados são lados da figura também. É calculado em graus sexagesimal por:

β = [180 (n-2)]/n

Ou em radianos usando:

β = [π (n-2)]/n

Ângulos externos

Eles são denotados pela carta grega γ. Na figura, observa -se que γ + β = 180º. Portanto:

γ = 180º - β

A soma de todos os ângulos externos a um polígono regular é 360º.

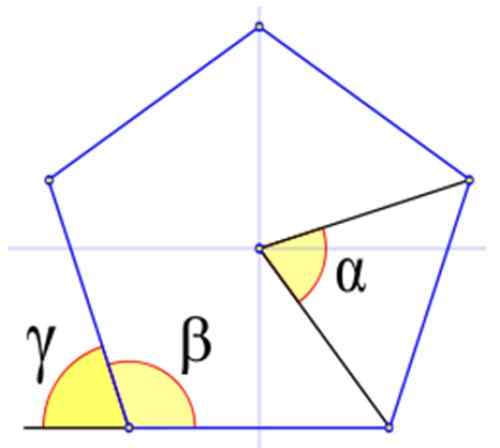Figura 4. Os ângulos em um polígono regular, neste exemplo um pentágono comum. Fonte: Wikimedia Commons.

Exemplos de polígonos regulares

Abaixo, temos os 8 primeiros polígonos regulares. Observamos que, à medida que o número de lados aumenta, o polígono se torna cada vez mais à circunferência em que eles são registrados.

Podemos imaginar que tornar o comprimento dos lados cada vez mais pequeno e aumentando o número deles, obtemos a circunferência.

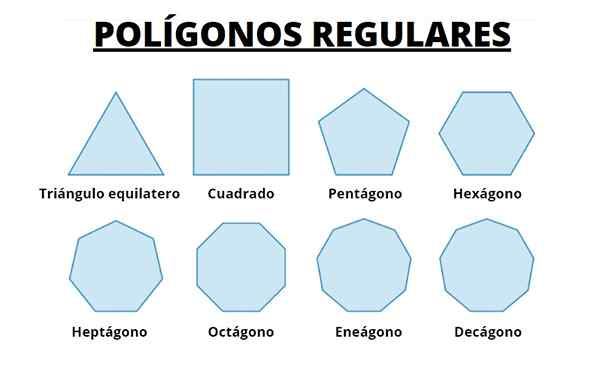Figura 5. Os oito primeiros polígonos regulares. Fonte: Wikimedia Commons.

- Polígonos regulares na vida diária e na natureza

Polígonos regulares são encontrados em toda parte na vida cotidiana e até na natureza. Vejamos alguns exemplos:

Sinais de trânsito

Na sinalização que vemos em rodovias e estradas abundam polígonos regulares, como triângulos equiláteis, quadrados e de Rhombus. Na Figura 6, vemos um sinal de alto sinal de forma.

Figura 5.- Sinal de trânsito com forma octogonal. Fonte: Pixabay.

Mobília

Inúmeras peças de móveis são quadradas, por exemplo, como uma figura geométrica característica, bem como muitas mesas, cadeiras e bancos são quadrados. Um paralelepípedo é geralmente uma caixa com lados em forma de retângulo (que não é um polígono comum), mas eles também podem fazer quadrados quadrados.

Arquitetura e construção

Os ladrilhos ou ladrilhos dos pisos e paredes, tanto em residências quanto nas ruas, geralmente têm a forma de polígonos regulares.

Os tesels são superfícies cobertas inteiramente com ladrilhos com figuras geométricas diversas. Com o triângulo, o quadrado e o hexágono podem ser feitos tesselves regulares, aqueles que usam apenas um único tipo de figura para revestir perfeitamente, sem espaços vazios (veja a Figura 6).

Além disso, os edifícios usam polígonos regulares em elementos como janelas e decoração.

Figura 6. Ladrilho quadrado. Fonte: Pixabay.

- Hexágonos regulares na natureza

Surpreendentemente, o hexagon regular é um polígono que aparece frequentemente na natureza.

Pode atendê -lo: distribuições discretas

Honeycombs feitos pelas abelhas para armazenar o mel tem uma forma muito aproximada para um hexágono comum. Como o Pappus de Alexandria observou, dessa maneira as abelhas otimizam o espaço para salvar o máximo de mel possível.

E também existem hexágonos regulares na concha de tartarugas e flocos de neve, que também adotam várias formas geométricas muito bonitas.

Exercício resolvido

Um hexágono regular faz parte de um semicírculo de 6 cm de raio, como mostrado na figura. Qual é o valor da área sombreada?

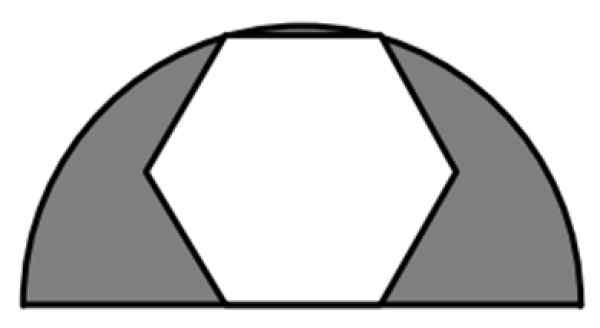Figura 7. Um hexágono regular registrado em um semicírculo. Fonte: f. Zapata.

Solução

A área sombreada é a diferença entre a área do semicírculo Radius r = 6 cm e a área hexagona completa, um polígono regular de 6 anos. Então, precisaremos de fórmulas para a área de cada uma dessas figuras.

Área semicírculo

PARA₁ = π r² /2 = π (6 cm)² /2 = 18π cm²

Área hexágona regular

A fórmula para calcular a área de um polígono regular é:

A = p.A /2

Onde P É o perímetro e para É o apothem. Como o perímetro é a soma dos lados, precisaremos do valor destes. Para hexágono regular:

P = 6ℓ

Portanto:

A = 6ℓa /2

Para encontrar o valor do lado ℓ É necessário construir figuras auxiliares, que explicaremos abaixo:

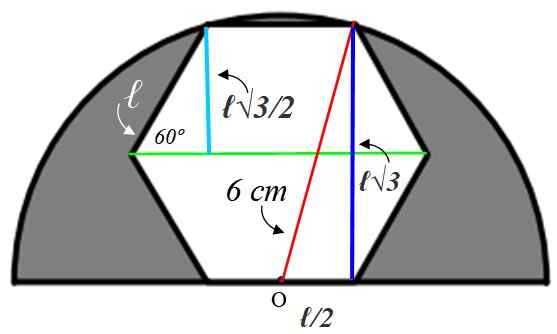
Vamos começar com o pequeno triângulo retângulo à esquerda, cuja hipotenusa é ℓ. Vale a pena um ângulo interno do hexágono:

α = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120º

O raio que desenhamos em bisecta verde esse ângulo, portanto o ângulo agudo do pequeno triângulo é 60º. Com as informações fornecidas, este triângulo é resolvido, encontrando o lado azul claro, que mede o mesmo que o apotem:

Cateto oposto = a = ℓ x sin 60º = ℓ√3 / 2 cm

Este valor é o dobro da perna azul escura do grande triângulo para a direita, mas daquele triângulo sabemos que a hipotenusa mede 6 cm porque é o raio do semicírculo. O Cateto restante (abaixo) vale ℓ/2 desde o ponto ou está no meio do lado.

Como os ângulos internos deste triângulo não são conhecidos, podemos elevar o teorema de Pitágoras para ele:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) /13 cm = 12 /√13 cm

Com este valor, o apotem é calculado:

a = ℓ√3 /2 cm = (12 /√13) x (√3 /2) cm = 6√3 /√13 cm

Vamos chamar um₂ para a área hexágona regular:

= 28. 8 cm²

Área de figura sombreada

PARA₁ - PARA₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Referências

1. Baldor, a. 1973. Geometria e trigonometria. Editorial cultural da América Central.
2. Desfrute de matemática. Tesels. Recuperado de: desfrutar.com.
3. E. PARA. 2003. Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
4. Hexágonos na natureza. Recuperado de: Malvargamath.WordPress.com.
5. Jiménez, r. 2010. Matemática II. Geometria e trigonometria. Segunda edição. Prentice Hall.
6. Polígonos regulares. Recuperado de: companheiro.Engenharia.USAC.Edu.Gt.
7. Wikipedia. Apótema. Recuperado de: é.Wikipedia.org.