Elementos Pentadecágono, Classificação, Características, Exercício

A PentadecAntagon É uma figura plana construída com quinze segmentos consecutivos e fechados. Este tipo de figuras é chamado polígono e eles são nomeados de acordo com a quantidade de lados que têm.

O triângulo, com três lados e o quadrilátero, de quatro, são exemplos de polígonos muito familiares, mas os polígonos podem ter mais lados.

figura 1.  Pentágono regular com vértices vermelhos. Fonte: Wikimedia Commons.

Os elementos básicos do Pentadecágono são os mesmos que qualquer polígono, independentemente da quantidade de lados que possui. Esses elementos são:

-Lados, que são os segmentos que compõem o pentadecágono por um total de 15.

-Vértices, Também 15, que são as extremidades dos lados adjacentes.

-Ângulos internos, Aqueles que são formados dentro do Pentadecágono entre dois lados adjacentes.

-Ângulos externos, formado entre um lado e o prolongamento de um dos lados consecutivos.

-Diagonais, Os segmentos de linha que se juntam a dois vértices não adjacentes.

[TOC]

Classificação

Um pentadecágono pode ser regular qualquer irregular, dependendo do tamanho de seus lados e da medida de seus ângulos internos. Se você tem todos os lados e os ângulos internos iguais -Quilátero e equiangle - é regular, como mostra a Figura 1, caso contrário, é irregular.

Também pode ser classificado como convexo qualquer côncavo. Um Pentágono côncavo tem um ou mais ângulos internos maiores que 180º, enquanto um sempre convexo tem ângulos internos inferiores a 180º. O Pentágono comum é convexo.

Outro critério de classificação é considerado se seus lados não consecutivos - ou suas extensões - forem cortados ou não. Quando eles não são cortados, como no caso da Figura 1, diz -se que é um pentadecágon simples. E se eles forem cortados, então é complexo.

Pode atendê -lo: geometria analítica

O Pentágono comum

O Pentágono regular, cujos lados e ângulos internos têm a mesma medida, é uma figura de grande simetria, porque os seguintes elementos adicionais são definidos aos descritos anteriormente:

-Centro: O ponto que a equidista dos vértices e dos lados.

-Rádio: A distância do centro para um dos vértices regulares do Pentágono.

-Ângulo central: Aquele que tem seu vértice no centro da figura e suas laterais passam por dois vértices adjacentes.

-Apótema, É o segmento perpendicular que se junta ao centro de um lado com o centro da figura.

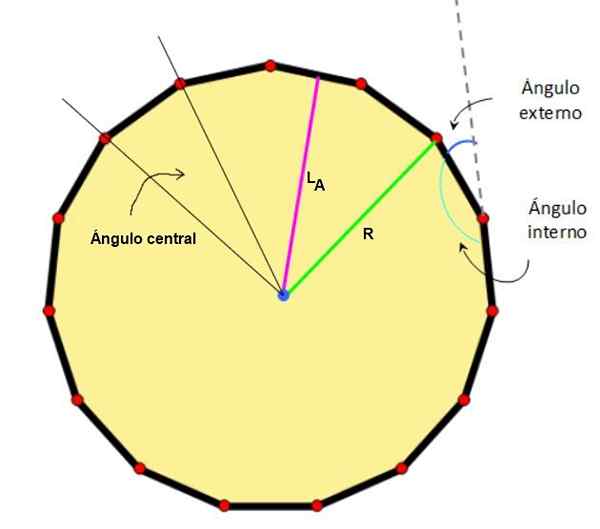Figura 2. Centro, apotem, rádio e ângulos notáveis ​​de um pentadecágono. Fonte: Wikimedia Commons/F. Zapata.

- Características do Pentágono Regular

Ângulos internos

A fórmula a seguir é usada para calcular a medida I dos ângulos internos de qualquer polígono regular, onde n É o número de lados:

Nesta fórmula, a medida que eu vem em graus, para expressá -la em Radianes, é multiplicada pelo fator π/180. Vamos ver qual é a medida dos ângulos internos do Pentágono comum, substituindo n = 15:

I = [(15-2) × 180º]/15 = 156º

Equivalente a 13π/15 radianos. Como os ângulos internos do Pentágono regular são menores de 180º, é um polígono convexo.

Soma de ângulos internos

É possível calcular a soma dos ângulos internos pela seguinte fórmula:

S = (n-2) x 180º

Como sempre, n representa o número de lados. Esta fórmula é válida para n = 3, 4, 5 .. .

Fazendo n = 15, obtemos:

S = (15 - 2) x 180º = 2340º

Ângulos externos

Um ângulo interno e um ângulo externo são suplementares, ou seja, sua soma é 180º, como observado na Figura 2. Portanto, um ângulo externo das medidas de Pentadecágono:

Pode servir a você: Binomial conjugado: como é resolvido, exemplos, exercícios

180 º - 156º = 24º.

Perímetro e área

O perímetro é a medida do contorno do polígono e está facilmente adicionando todos os lados. Sim para É o comprimento do lado, basta se multiplicar por n, O número de lados.

Para um pentágono regular do lado a, o perímetro P é:

P = 15a

Se for uma figura irregular, na qual a medida dos lados difere, o perímetro está adicionando o comprimento de todos os seus lados.

Quanto à área, podemos calculá -la de várias maneiras. Por exemplo, temos a fórmula que permite obtê -la sabendo o comprimento de seus lados:

Executando as operações indicadas, ele permanece aproximadamente:

A = 17.6426⋅A²

Há outra opção, aplicável a polígonos regulares. Trata -se de dividi -los em triângulos básicos iguais ao polígono para. A altura do triângulo é o comprimento do apothem l_PARA, definido acima.

A área do referido triângulo é calculada com a fórmula bem conhecida: base x altura /2. Dessa maneira, a área de triângulo único é:

Área = a. eu_PARA /2

Para ter a área total do polígono, basta se multiplicar pelo número de lados n, que neste caso é 15:

A = 15⋅A⋅ L_PARA /2

E como o perímetro da figura é p = 15⋅A, então:

A = P⋅ L_PARA /2

Diagonais

As diagonais são os segmentos que unem dois vértices não consecutivos, como afirmado acima. Saber quantas diagonais um polígono regular tem de n Lados, incluindo Pentadecágono, há a seguinte fórmula:

Onde d é o número de diagonais.

Agora substituímos n = 15, para obter o total de diagonais:

Pode atendê -lo: polígonos regulares: propriedades, elementos, ângulos, exemplos

D = [15 × (15-3)]/2 = 90 diagonais.

Construção com regra e bússola

Pentadecágono é construído com regra e bússola a partir de uma circunferência. O 360º deve ser dividido em 15 partes iguais de 24º. Primeiro, as construções auxiliares indicadas na animação são realizadas para obter um ângulo de 60º, que é dividido por 36º e 24º.

Figura 3. Construção com regra e bússola de um pentágono comum. Fonte: Wikimedia Commons.

Exercício resolvido

Se o perímetro de um pentadecágono registrado em um círculo de raio r é de 12,56 cm. Calcular:

a) o rádio.

b) sua área.

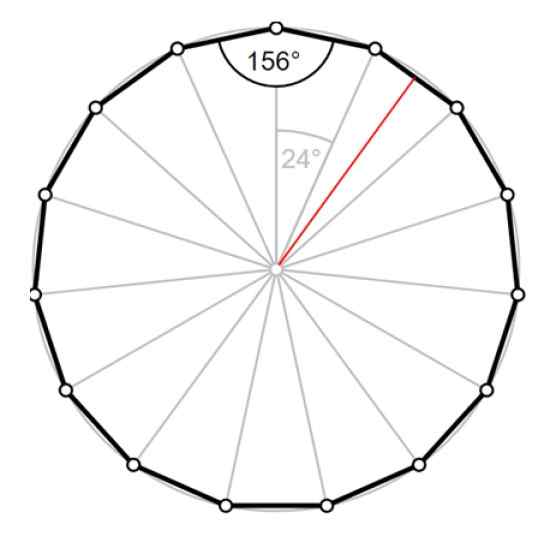Figura 4. Pentadecágono: ângulo central, ângulo interno e apotema vermelho. Fonte: Wikimedia Commons/F. Zapata.

Solução para

O perímetro é p = 15⋅A = 12.56 cm, portanto o lado de pentadecágono é 0.8373 cm. O rádio Podemos calculá -lo com a ajuda de um dos triângulos na Figura 4.

O apothem l_PARA corresponde à altura do triângulo, desenhado em vermelho, que divide o ângulo de 24º em dois ângulos de 12º.

Existem dois triângulos certos com um ângulo interno de 12º cada, e para qualquer um deles, podemos aplicar trigonometria para encontrar a hipotenusa, que é o comprimento r do raio.

Desta maneira:

sen 12º = (a /2) /r

R = (a /2) /sen 12º = (0.8373 cm / 2) / sen12º = 2.01 cm.

Solução b

Podemos calcular a área de Pentadecágono usando a fórmula:

A = P⋅ L_PARA /2

Já sabemos o perímetro p = 12.56 cm e o comprimento do apotem é calculado pela tangente ou pelo cosseno 12º:

Cos 12º = L_PARA / R

eu_PARA = R. cos 12 º = 2.01 cm. cos 12 º = 1.97 cm

Substituindo:

A = 12.56 cmulas 1.97 cm /2 = 12.35 cm²

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Aprenda matemática. Figuras geométricas. Recuperado de: Rodrigoanchorena.WixSite.com.
3. Sangaku Maths. Elementos de um polígono e sua classificação. Recuperado de: sangakoo.com.
4. Wikipedia. Pentadecágono. Recuperado de: é.Wikipedia.org.
5. Wolfram Math World. Pentadecagon. Recuperado de: Mathworld.Volfrâmio.com.