Par ordenado

O que é um par ordenado?

Um par ordenado ou duo É um conjunto de dois elementos que são escritos de acordo com a ordem estabelecida por um determinado critério. O referido critério especifica qual dos dois elementos vai primeiro e qual deles vai atrás.

O par ordenado é indicado como (x, y), onde "x" é o primeiro elemento do par e "y" é o segundo, também chamado Componentes. Em geral (x, y), não é o mesmo torque arrumado (y, x). Além da ordem, outra característica importante dos pares ordenados é a igualdade: dois pares ordenados (a, b) e (c, d) são os mesmos apenas se a = c e b = d.

figura 1.- Graças aos pares arrumados, o filhote sabe que os ossos estão enterrados nos locais (3,1) e (-4,2), enquanto sua casa está em (0,0). Fonte: f. Zapata.

Exemplos de pares ordenados seriam aqueles que são compostos de idade e o peso de um curso de estudantes de matemática. O par ordenado (15, 62) corresponde a um aluno de 15 anos, diferente do par improvável (62,15).

O conceito de torque ordenado é muito importante em várias áreas da matemática, como o avião cartesiano, frações, vetores no avião, relacionamentos e funções. Um aspecto importante é que seus elementos não têm necessariamente numéricos, por exemplo, eles podem ser ordenados com:

• País da cidade
• Nome sobrenome
• Esposa esposo

E muitas outras combinações.

Exemplos de pares ordenados

Frações

Uma fração é representada como o quociente de dois números inteiros P/Q, por exemplo, a fração ½, que é equivalente ao número decimal 0.5.

No entanto, essa fração não é a única que representa o decimal 0.5, assim como o seguinte:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2)…

Dessa maneira, qualquer fração pode ser representada como um par ordenado (p, q), onde p e q são inteiros, com P ocupando a posição do numerador e Q a do denominador. Há uma restrição importante e que q (o denominador) deve ser diferente de 0, uma vez que as frações da forma p/0 não são definidas.

Pode atendê -lo: conjunto finito: propriedades, exemplos, exercícios resolvidos

E outra condição importante é que duas frações A/B e C/D são iguais desde que sejam cumpridas que:

A ∙ d = b ∙ c

Funções e seus gráficos

Uma função pode ser expressa como um conjunto de pares arrumados. Por exemplo, ao representar graficamente uma função no plano cartesiano, o primeiro elemento recebe a posição da variável independente, enquanto a segunda é atribuída a variável dependente. Este é um par ordenado.

Para a função y = f (x), o torque arrumado pode ser expresso como [x, f (x)]]. Por exemplo, considere o conjunto inicial:

A = 1, 2, 3, 4

Neste conjunto, existem os primeiros componentes de um par ordenado de acordo com a função y = x². O conjunto dos segundos componentes é:

B = 1, 4, 9, 16

E os pares ordenados são formados são:

(1,1); (2,4); (3, 9); (4; 16)

Respeito.

Vetores no avião

Os vetores podem ser representados no plano cartesiano por pares ordenados, onde o primeiro elemento representa o componente horizontal "X" e o segundo o componente vertical "y". Para distinguir os vetores dos pontos do avião, eles são denotados por letras em negrito e os colchetes são usados ​​em vez dos parênteses, assim:

v =

Por exemplo, o vetor v = tem um componente horizontal igual a 4 e componente vertical igual a 7. Seu gráfico é:

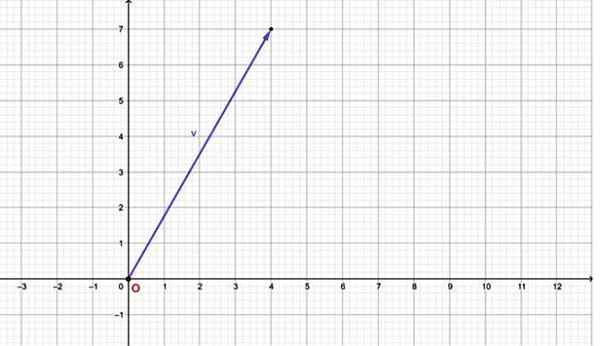Figura 2.- Um vetor plano pode ser expresso através de um par ordenado. Fonte: f. Zapata.

Observe que este vetor tem sua origem coincidindo com a origem do sistema de coordenadas (0,0). Se o vetor tiver sua origem em qualquer outro ponto, ele também poderá ser expresso na forma de um torque ordenado através de um par de ordenados, para fazer isso, veja as seguintes seções.

Pode atendê -lo: hierarquia de operações

Operações de Pares ordenadas

Adição

Deixe os alvos (a, b) e (c, d) ser pares (d). Um novo torque é obtido por meio de sua soma de acordo com:

(a, b)+(c, d) = (a+c, b+d)

Elemento neutro

O elemento neutro da adição de pares ordenados é o torque (0,0), pois quando adiciona ao par ordenado (a, b), a soma é a última:

(a, b) + (0,0) = (a, b)

Soma do oposto

Ao adicionar um par ordenado (a, b) com seu oposto (-a, -b), o torque ordenado (0,0) é obtido:

(a, b) + (-a, -b) = (0,0)

Comunicação

A ordem das adições não altera a soma:

(a, b) + (c, d) = (c, d) + (a, b)

Associatividade

O resultado da adição de três pares ordenados não é alterado quando agrupado para executar a operação:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Subtração de pares ordenados

Deixe os alvos (a, b) e (c, d) ser, a subtração é realizada da seguinte forma:

(a, b)-(c, d) = (a-c, b-d)

produtos

No produto, existem duas opções: i) Multiplique um torque ordenado por uma constante e ii) multiplique duas (ou mais) boatos.

Multiplicação por uma constante

Seja k uma constante e o torque ordenado (a, b), o produto entre a constante e o torque é:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Multiplicação de pares ordenados

O produto entre os pares ordenados (a, b) e (c, d) é realizado da seguinte forma:

(a, b) x (c, d) = (ac - bd, bc+ad)

Elemento neutro

O elemento neutro da multiplicação é (1.0), pois, multiplicando qualquer torque ordenado por isso, seguindo a regra de multiplicação descrita acima, o torque original é:

(a, b) x (1,0) = (a - 0, b + 0) = (a, b)

Pode servir a você: inverso multiplicativo: explicação, exemplos, exercícios resolvidos

Associatividade

Como a ordem dos fatores não altera o produto, ele pode ser agrupado de maneiras diferentes para multiplicar três ou mais pares arrumados e o resultado é o mesmo:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Exercícios resolvidos

Exercício 1

Você pediu pares (x², X-2) = (16, 2). Qual é o valor de x?

Solução

A aplicação da igualdade de pares ordenados é obtida primeiro:

x² = 16 ⇒ x₁ = 4, x₂ = -4

Para saber qual dos dois valores escolhem, uso de:

X-2 = 2

x = 2 + 2 = 4

Portanto, o valor solicitado de x é 4.

Exercício 2

Expresse como um par de ordenado o vetor que vai do ponto (1, 3) ao ponto (7, 11) e o representa graficamente.

Solução

Ser v O vetor pesquisado. Para determinar o par ordenado que o representa e que contém suas coordenadas, as coordenadas do ponto de chegada e o ponto de origem são subtraídas, nessa ordem. Então:

v = =

O vetor é então representado v como aquele que vai de (1,3) a (7, 11) e o equipamento v cuja origem é fixada à origem do sistema de coordenadas (0,0). Como você pode ver, eles têm a mesma direção e significado.

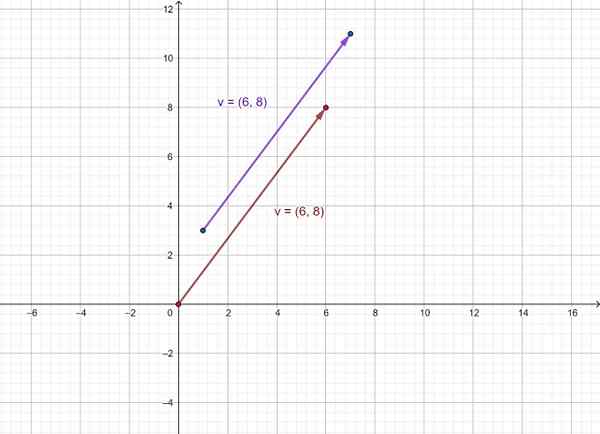Figura 3. Representação de um vetor como um par ordenado. Fonte: f. Zapata.

Referências

1. Deepal. Par ordenado. Recuperado de: Deepai.org.
2. Mathemovil. Representação cartesiana de um vetor por um par ordenado. Recuperado de: Matemovil.com.
3. Tutors do time do colégio. Par ordenado. Recuperado de: WarsityTorm.com
4. Priestri, Juan. Relacionamentos e funções. Faculdade de Engenharia. Departamento de Matemática. Universidade de Buenos Aires. Recuperado de: assuntos.fi.Uba.ar.
5. Universidade de Denver. Relações. Recuperado de: matemática.Ucdenver.Edu.