Recursos de ondas senoidais, peças, cálculo, exemplos

As ondas senoidais São padrões de ondas que podem ser descritos matematicamente pelas funções seno e cosseno. Eles descrevem, com razão, eventos naturais e sinais variáveis ​​no tempo, como tensões geradas por usinas elétricas e depois usadas em residências, indústrias e ruas.

Elementos elétricos, como resistências, capacitores e indutâncias, que se conectam a entradas de tensão sinusoidais, também produzem respostas também senoidal. A matemática usada em sua descrição é relativamente simples e foi completamente estudada.

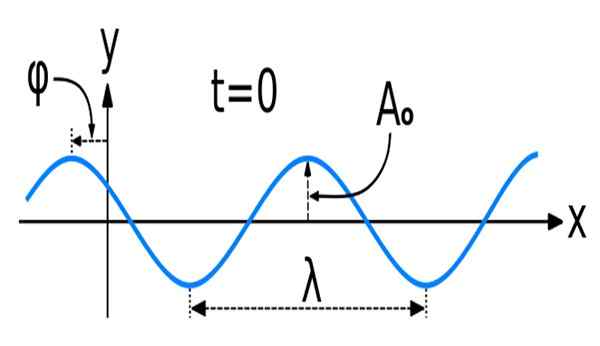
figura 1. Uma onda senoidal com algumas de suas principais características espaciais: amplitude, comprimento de onda e fase. Fonte: Wikimedia Commons. WAVE_NEW_SINE.SVG: Kraaiennestoriginalmente criado como uma onda de cosseno, por usuário: PELEGS, como arquivo: Wave_new.Trabalho SVGDerivative: Dave3457 [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenças/BY-SA/3.0)]

A matemática das ondas sinusoidais ou sinusoidais, como elas também são conhecidas, é a das funções seno e cosseno.

Essas são funções repetitivas, o que significa periodicidade. Ambos têm da mesma maneira, com a condição de que o cosseno é deslocado para a esquerda em relação à mama em uma sala de ciclo. É observado na Figura 2:

Figura 2. As funções sen x e cos x são deslocadas uma em relação ao outro. Fonte: f. Zapata.

Então cos x = sin (x + π/2). Com a ajuda dessas funções, uma onda seno. Para fazer isso, a magnitude em questão é colocada no eixo vertical, enquanto no eixo horizontal está localizado.

A qualidade repetitiva dessas funções também é apreciada no gráfico acima: o padrão é repetido continuamente e regularmente. Graças a essas funções, você pode expressar tensões e correntes do tipo siniano variando com o tempo, colocando no eixo vertical em vez do e, a v ou um Yo para representar tensão ou corrente e no eixo horizontal em vez do x, O t do tempo.

A maneira mais geral de expressar uma onda senoidal é:

v (t) = V_m pecado (ωT+φ)

Em seguida, aprofundaremos o significado dessa expressão, definindo alguns termos básicos para caracterizar a onda senoidal.

[TOC]

Festas

Período, amplitude, frequência, ciclo e fase são conceitos se aplicam a ondas periódicas ou repetitivas e são importantes para caracterizá -las adequadas.

Período

Uma função periódica como as mencionadas, que é repetida em intervalos regulares, sempre atende à seguinte propriedade:

f (t) = f (t + t) = f (t + 2t) = f (t + 3t) =… .

Onde T É uma quantidade chamada aceno, E é o tempo necessário para repetir uma fase do mesmo. Nas unidades do sistema internacional, o período é medido em segundos.

Amplitude

De acordo com a expressão geral da onda senoidal v (t) = V_m sin (ωt+φ), v_m É o valor máximo da função, que ocorre quando sin (ωt+φ) = 1 (Lembrando que o maior valor que o seio e a função cosseno admite ambos é 1). Este valor máximo é precisamente o Amplitude de onda, também conhecido como amplitude de pico.

No caso de uma tensão, será medido em volts e, se for uma corrente, estará em amplificadores. Na onda seno.

Pode servir a você: Termômetro de resistência: características, operação, usos

Ciclo

Faz parte da onda contida em um período. No número anterior, o período foi tomado medindo -o de dois picos ou sulcos consecutivos, mas pode começar a ser medido a partir de outras partes da onda, enquanto são limitadas por um período.

Nota na figura a seguir, como um ciclo tampa de um ponto para outro com o mesmo valor (altura) e a mesma inclinação (inclinação).

Figura 3. Em uma onda senoidal, um ciclo sempre ocorre por um período. O importante é que o ponto de partida e o fim estão na mesma altura. Fonte: Boylestad. Introdução à análise do circuito. Pearson.

Frequência

É a quantidade de ciclos que ocorrem em 1 segundo e está ligada ao argumento da função sinusal: ωt. A frequência é indicada como F E é medido em ciclos por segundo ou Hertz (Hz) no sistema internacional.

A frequência é a quantidade inversa do período, portanto:

F = 1/t

Enquanto frequência F está relacionado ao Frequência angular ω (pulsação) como:

Ω = 2πF

A frequência angular é expressa em Radianes /segundo no sistema internacional, mas os radianos não têm dimensão, portanto a frequência F e frequência angular Ω Eles têm as mesmas dimensões. Observe que o produto ωt dá radianos como resultado e deve ser levado em consideração ao usar a calculadora para obter o valor de Sen ωt.

Estágio

Corresponde ao deslocamento horizontal experimentado pela onda, com relação a um tempo gasto como referência.

Na figura seguinte, a onda verde é avançada em relação ao vermelho em um tempo t_d. Duas ondas sinusoidais estão em Estágio Quando sua frequência e fase são iguais. Se a fase difere, então eles estão em brecha. Figura 2 ondas também estão desatualizadas.

Figura 4. Ondas sinusidais pelo pelotão. Fonte: Wikimedia Commons. Nenhum autor legível por máquina fornecido. Kanjo ~ Commonswiki assumiu (com base em reivindicações de direitos autorais). [Domínio público].

Se a frequência das ondas for diferente, elas estarão em fase quando a fase ωt+φ Seja o mesmo nas duas ondas em certos momentos.

Gerador de ondas senoidal

Existem muitas maneiras de obter um sinal em forma de seno. Executões caseiros fornecem -lhes.

Aplicação da lei de Faraday

Uma maneira bastante simples de obter um sinal seno. Isso indica que em um circuito fechado de corrente, por exemplo, um loop, colocado no meio de um campo magnético, uma corrente induzida é gerada quando o campo magnético flui através dele muda com o tempo. Consequentemente, a Tensão induzida qualquer FEM induzido.

O fluxo do campo magnético varia se o loop for girado com rapidez angular constante no meio do campo criado entre os pólos n e s do ímã mostrado na figura.

Pode atendê -lo: Netuno (planeta)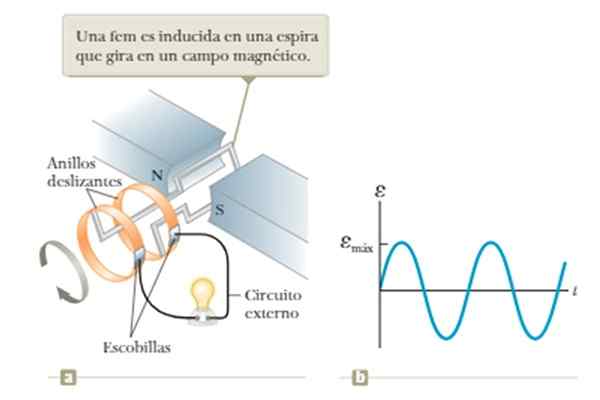Figura 5. Gerador de ondas baseado na lei de indução de Faraday. Fonte: Fonte: Raymond A. Serway, Jonh W. Jewett [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenças/BY-SA/4.0)].

A limitação deste agente é a dependência da tensão obtida com a frequência de rotação do loop, como será visto em mais detalhes no Exemplo 1 da seção de exemplos posteriormente.

Oscilador de Wien

Outra maneira de obter uma onda seno. Dessa forma, são obtidas ondas senoida.

A figura mostra um gerador de sinal senoidal, com o qual outras formas de onda também podem ser obtidas: triangular e quadrados, entre outros.

Figura 6. Um gerador de sinal. Fonte: Fonte: Wikimedia Commons. Opgreg na Wikipedia inglesa [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenças/BY-SA/3.0)].

Como calcular ondas senoidais?

Para realizar cálculos que envolvem ondas seno. Essas calculadoras têm modos para trabalhar os ângulos em graus ou Radianes, e é fácil converter de uma maneira para a outra. O fator de conversão é:

180 º = π Radianes.

De acordo com o modelo da calculadora, você deve navegar através da tecla de modo para encontrar a opção de grau, que permite trabalhar em funções trigonométricas em graus, ou a opção RAD, para trabalhar diretamente os ângulos em Radianes.

Por exemplo, pecado 25 º = 0.4226 com a calculadora colocada no modo deg. Ao converter 25 º para Radianes, você recebe 0.4363 Radianes e sen 0.4363 rad = 0.425889 ≈ 0.4226.

O osciloscópio

O osciloscópio é um aparelho que permite visualizar em uma tela sinais de tensões e correntes alternativas e diretas. Possui botões para ajustar o tamanho do sinal em uma grade, como mostrado na figura a seguir:

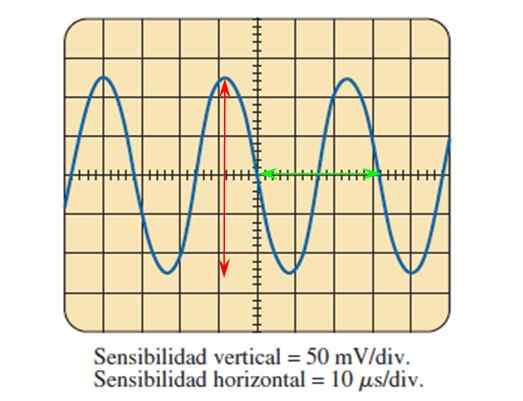Figura 7. Um sinal sinusoidal medido com um osciloscópio. Fonte: Boylestad.

Através da imagem fornecida pelo osciloscópio e conhecendo o ajuste da sensibilidade em ambos os eixos, é possível calcular os parâmetros de onda descritos acima.

Pode atendê -lo: galáxias elípticas: formação, características, tipos, exemplos

A figura mostra o sinal de tensão senoidal em função do tempo, no qual cada divisão do eixo vertical vale 50 milivolts, enquanto no eixo horizontal, cada divisão vale 10 microssegundos.

A amplitude de pico a pico é contar as divisões que a onda abrange verticalmente, ajudando com a seta vermelha:

5 divisões são contadas com a ajuda da seta vermelha, de modo que a tensão de pico de pico é:

V_pp = 5 divisões x 50 mV/divisão = 250 mV.

Tensão pico V_p É medido no eixo horizontal, sendo 125 mV.

Para encontrar o período em que um ciclo é medido, por exemplo, o delimitado pela Arqueiro Verde, que cobre 3.2 divisões, então o período é:

T = 3.2 divisões x 10 microssegundos/divisão = 32 microssegundos = 32 μs

Exemplos

Exemplo 1

Para o gerador na Figura 3, demonstre da lei de Faraday que a tensão induzida tem seno. Suponha que o loop consista em n voltas em vez de um, tudo com a mesma área A e está girando com rapidez angular constante ω no meio de um campo magnético B uniforme.

Solução

A lei de Faraday diz que o FEM induzido ε é:

ε = -n (dφ_B /dt)

Onde Φ_B É o fluxo do campo magnético, que será variável, pois depende de como o loop é exposto ao campo a cada momento. O sinal negativo simplesmente descreve o fato de que esse FEM se opõe à causa que a produz (Lei de Lenz). O fluxo devido a um único loop é:

Φ_B = B.PARA.cos θ

θ é o ângulo que o vetor normal do plano do loop está se formando com o campo B À medida que a rotação ocorre (veja a figura), esse ângulo varia naturalmente como:

θ = ωt

De maneira que: Φ_B = B.PARA.cos θ = b.PARA.cos ωt. Agora você só precisa derivar essa expressão em relação ao tempo e, com ela, o FEM induzido é obtido:

ε = -n.d (b.PARA.cos ωt) /dt

Como o campo B É uniforme e a área da SPASE não varia, eles deixam a derivada:

ε = -NBA. D (cos ωt) /dt = ωnba. Sen ωt

Exemplo 2

Um loop tem uma área de 0.100 m² e virar para 60.0 REV/S, com seu eixo de rotação perpendicular a um campo magnético uniforme de 0.200 t. Sabendo que a bobina tem 1000 voltas para encontrar: a) o FEM máximo que é gerado, b) a orientação da bobina em relação ao campo magnético quando o FEM máximo induzido ocorre.

Figura 8. Uma espiral de n voltas quebradas no meio de um campo magnético uniforme e gera um sinal seno. Fonte: r. Serway, Física para Ciência e Engenharia. Volume 2. Cengage Learning.

Solução

a) O máximo feminino é ε_Máx = Ωnba

Antes de prosseguir para substituir os valores, a frequência de 60 rotações/s para unidades do sistema internacional deve ser passada. Sabe -se que 1 Revolução é equivalente a uma curva ou 2p Radianes:

60.0 REV/S = 120P RADIANES/S

ε_Máx = 120p Radianes x 1000 voltas x 0.200 t x 0.100 m² = 7539.82 V = 7.5 kV

b) Quando esse valor ocorre Sen ωt = 1 portanto:

ωt = θ = 90º,

Nesse caso, o plano espiral é paralelo a B, de modo que o vetor normal para o referido plano se forma 90º com o campo. Isso ocorre quando o vetor preto na Figura 8 é perpendicular ao vetor verde que representa o campo magnético.

Referências

1. Boylestad, r. 2011. Introdução à análise do circuito. 12º. Edição. Pearson. 327-376.
2. Figueroa, d. 2005. Eletromagnetismo. Série física para ciência e engenharia. Volume 6. Editado por d. Figueroa. Universidade de Simon Bolivar. 115 e 244-245.
3. Figueroa, d. 2006. Laboratório de Física 2. Equinox editorial. 03-1 e 14-1.
4. Ondas senoidais. Recuperado de: iessierradegara.com
5. Serway, r. 2008.Física para Ciência e Engenharia. Volume 2. Cengage Learning. 881-884