Números transcendentes que são, fórmulas, exemplos, exercícios

O números transcendentes Eles são aqueles que não podem ser obtidos como resultado de uma equação polinomial. O oposto de um número transcendente é um Número algébrico, que são soluções de uma equação polinomial do tipo:

para_n xⁿ + para_N-1 x^N-1 +… + A₂ x² + para₁ x + a₀ = 0

Onde os coeficientes para_n, para_N-1,… para₂, para₁, para₀ São números racionais, chamados Coeficientes polinomiais. Se um número x é uma solução da equação anterior, esse número não será transcendente.

figura 1. Dois números de grande importância na ciência são números transcendentes. Fonte: Public DomainParturas.líquido.

Analisaremos alguns números e veremos se eles são ou não transcendentes:

a) 3 não é transcendente porque é uma solução de x - 3 = 0.

b) -2 não pode ser transcendente porque é uma solução de x + 2 = 0.

c) ⅓ é 3x - 1 = 0 solução

d) uma solução de equação x² - 2x + 1 = 0 é √2 -1, então o referido número por definição não é transcendente.

e) Nem é √2 porque é o resultado da Equação X² - 2 = 0. Ao levantar √2 quadrado, resulta em 2, que subtraído de 2 não importa para zero. Então √2 é um número irracional, mas não é transcendente.

[TOC]

O que são números transcendentes?

O problema é que não há regra geral para obtê -los (mais tarde, diremos uma forma), mas alguns dos mais famosos são o número pi e ele Número Neper, denotado respectivamente por: π e e.

O número π

O número π Parece naturalmente observando que o quociente matemático entre o perímetro P de um círculo e seu diâmetro D, independentemente de ser um círculo pequeno ou grande, sempre dá o mesmo número, chamado pi:

π = P/D ≈ 3.14159…

Isso significa que, se o diâmetro da circunferência for tomado como uma unidade de medição, para todos eles, grandes ou pequenos, o perímetro sempre valerá p = 3,14… = π, Como pode ser visto na animação da Figura 2.

Pode servir você: Teorema de Bolzano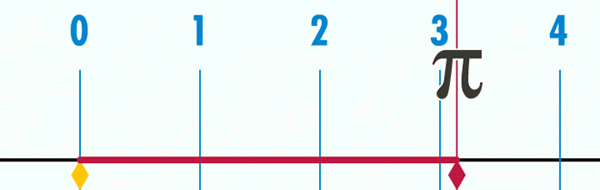Figura 2. O comprimento do perímetro de um círculo às vezes é o comprimento do diâmetro, sendo aproximadamente 3,1416.

Para determinar mais decimais, você deve medir mais precisão P e D e depois calcular o quociente, o que foi feito de maneira matemática. A conclusão é que os decimais do quociente não têm fim e nunca são repetidos, de modo que o número π Além de ser transcendente, também é irracional.

Um número irracional é esse número que não pode ser expresso como a divisão de dois números inteiros. 

Sabe -se que todo número transcendente é irracional, mas não é verdade que todos irracionais são transcendentes. Por exemplo √2 é irracional, mas não é transcendente.

Figura 3. Os números transcendentes são irracionais, mas a declaração recíproca não é verdadeira.

O número e

O número transcendente é a base dos logaritmos neperianos e sua abordagem decimal é:

e ≈ 2.718281828459045235360… .

Se você quisesse escrever o número e Exatamente, seria necessário escrever infinitos decimais, porque todo número transcendente é irracional, como dito antes.

Os dez primeiros dígitos de e Eles são fáceis de lembrar:

2.7 1828 1828 E embora pareça seguir um padrão repetitivo, isso não é alcançado nas decimais de ordem maior que nove.

Uma definição mais formal de e É o seguinte:

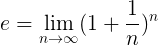
O que significa que o valor exato de e A operação indicada nesta fórmula é alcançada, quando o número natural n Tende ao infinito.

Isso explica por que só podemos obter abordagens para e, Como por mais grande o número n ser colocado, você sempre pode encontrar um n idoso.

Vamos procurar algumas abordagens por conta própria:

-Quando n = 100 então (1 + 1/100)¹⁰⁰ = 2.70481 que mal coincide no primeiro decimal com o valor "verdadeiro" de e.

-Se você é escolhido n = 10.000 você tem (1 + 1/10.000)^10.000 = 2.71815 que coincide com o valor "exato" de E nos três primeiros decimais.

Pode atendê -lo: lados homólogos

Este processo deve ser seguido para poder obter o valor "verdadeiro" de e. Acho que não temos tempo para alcançá -lo, mas vamos fazer mais uma tentativa:

Vamos usar n = 100.000:

(1 + 1/100.000)^100.000 = 2.7182682372

Que ele tem apenas quatro decimais coincidindo com o valor considerado preciso.

O importante é entender que quanto maior o valor de n escolhido para calcular e_n, mais próximo será do valor verdadeiro. Mas esse valor verdadeiro só será mantido quando n for infinito.

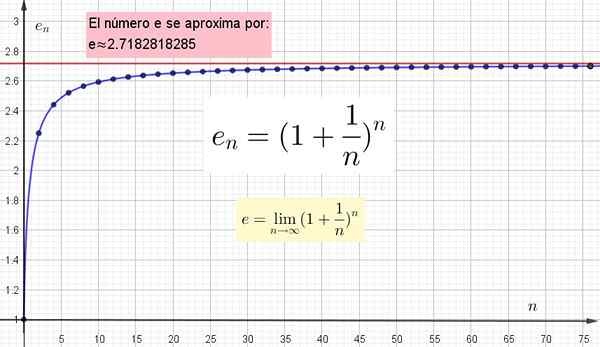Figura 4. É mostrado graficamente como o valor mais alto de n é mais próximo de e, mas para atingir o valor exato n deve ser infinito.

Outros números transcendentes

Além desses números famosos, existem outros números transcendentes, por exemplo:

- 2^√2

Qualquer número algébrico, que não é 0 ou 1, elevado a um expoente irracional será um número transcendente.

-Número 10 de Champernowne: 

C_10 = 0,123456789101112131415161718192021… .

-O número de Champernowne na base 2:

C_2 = 0,110111001011011… .

-O número γ ou gama constante de Euler-Mascheroni:

γ ≈ 0,577 215 664 901 532 860 606

Que é obtido fazendo o seguinte cálculo:

γ ≈ 1 + ½ + ⅓ + ¼ +… + 1/n - ln (n)

Para quando n Seja muito grande. Para ter o valor exato do número gama, seria necessário calcular com n infinito. Algo semelhante ao que fizemos acima.

E há muitos outros números transcendentes. O grande matemático Georg Cantor, nascido na Rússia e viveu entre 1845 e 1918, mostrou que o conjunto de números transcendentes é muito maior que o conjunto de números algébricos.

Fórmulas onde o número transcendente π aparece

O perímetro da circunferência

P = π d = 2 π r, onde p é o perímetro, d o diâmetro e r o raio da circunferência. Deve -se lembrar que:

Pode atendê -lo: quanto você precisa adicionar a 3/4 para obter 6/7?

-O diâmetro da circunferência é o segmento mais longo que se junta a dois pontos e que sempre passa pelo seu centro,

-O raio é metade do diâmetro e é o segmento que vai do centro para a borda.

Área circular

A = π r² = ¼ π D²

Superfície de uma esfera

S = 4 π r^2.

Sim. Embora não pareça, a superfície de uma esfera é a mesma que a de quatro círculos do mesmo raio que a esfera.

Volume da esfera

V = 4/3 π r³

Exercícios

- Exercício 1

A pizzaria "exótica" vende pizzas de três diâmetro: 30 cm pequenos, mediana de 37 cm e 45 cm. Uma criança está com muita fome e percebeu que duas pequenas pizzas têm o mesmo custo que um grande. O que será melhor para ele, compre duas pequenas pizzas ou uma grande?

Figura 5.- A área de uma pizza é proporcional ao quadrado do raio, sendo a constante de proporcionalidade. Fonte: Pixabay.

Solução

Quanto maior a área, maior a quantidade de pizza, por esse motivo, a área de uma pizza grande será calculada e comparada à de duas pequenas pizzas:

Grande área de pizza = ¼ π D² = ¼ ⋅3,1416⋅45² = 1590,44 cm²

Pequena área de pizza = ¼ π D² = ¼ ⋅3,1416⋅30² = 706,86 cm²

Portanto, duas pequenas pizzas terão uma área de 

2 x 706,86 = 1413,72 cm² .

É claro: haverá mais pizza comprando um único de dois pequenos.

- Exercício 2

A pizzaria "exótica" também vende um raio de 30 cm semi -homem -pizza para a mesma forma retangular de 30 x 40 cm. Qual você escolheria?

Figura 6.- A superfície de um semi -falador é o dobro da superfície circular da base. Fonte: f. Zapata.

Solução

Conforme declarado na seção anterior, a superfície de uma esfera é quatro vezes maior que a de um círculo do mesmo diâmetro; portanto, um semi -lide de 30 cm de diâmetro terá:

30 cm semi -homem -pizza: 1413,72 cm² (duas vezes uma circular do mesmo diâmetro)

Pizza retangular: (30 cm) x (40 cm) = 1200 cm² .

Semi -homem -pizza tem uma área maior.

Referências

1. Fernández J. O número e. Origem e curiosidades. Recuperado de: matemática de soja.com
2. Desfrute de matemática. Número de Euler. Recuperado de: desfrutar.com.
3. Figuera, j. 2000. Matemática 1ª. Diversificado. Edições Co-Bo.
4. Garcia, m. O número e no cálculo elementar. Recuperado de: matemática.Ciens.Ucv.ir.
5. Wikipedia. Número PI. Recuperado de: Wikipedia.com
6. Wikipedia. Números transcendentes. Recuperado de: Wikipedia.com