Número de Euler ou número e quanto vale, propriedades, aplicações

Ele Número Euler ou Número E É uma constante matemática bem conhecida que aparece com frequência em numerosas aplicações científicas e econômicas, juntamente com o número π e outros números importantes em matemática.

Uma calculadora científica lança o seguinte valor para o número e:

figura 1. O número de Euler aparece freqüentemente na ciência. Fonte: f. Zapata.

E = 2.718281828…

Mas muitos outros decimais são conhecidos, por exemplo:

E = 2.71828182845904523536…

E computadores modernos permitiram trilhões decimais ao número e.

É um número irracional, O que significa que ele tem uma quantidade infinita de decimais sem qualquer padrão repetitivo (a sequência 1828 aparece duas vezes no início e não se repete mais).

E também significa que o número E não pode ser obtido como o quociente de dois números inteiros.

[TOC]

História

O número e Ele foi identificado pelo cientista Jacques Bernoulli em 1683, quando estudou o problema de interesse composto, mas anteriormente ele apareceu indiretamente nas obras do matemático escocês John Napier, que inventou os logaritmos para 1618.

No entanto, foi Leonhard Euler em 1727 quem lhe deu o nome e o nome e estudou intensivamente suas propriedades. É por isso que também é conhecido como o Número Euler e também como uma base natural para os logaritmos neperianos (um expoente) usados.

Quanto vale o número E?

O número E Vale:

E = 2.71828182845904523536…

Os pontos suspeitos significam que há uma quantidade infinita de decimais e, de fato, milhões deles são conhecidos com computadores atuais.

Representações do número E

Existem várias maneiras de definir e que descrevemos abaixo:

O número e como um limite

Uma das várias maneiras pelas quais o número E é expresso é o que o cientista Bernoulli encontrou em seu trabalho sobre o interesse composto:

Em que você tem que fazer o valor n Um número muito grande.

É fácil verificar, com a ajuda de uma calculadora, que quando quando n É muito grande, a expressão anterior tende ao valor de e dado anteriormente.

Pode servir a você: Função Bijectiva: O que é, como é feito, exemplos, exercícios

Claro que podemos nos perguntar o tamanho disso n, Então, tentamos com números redondos, como estes, por exemplo:

n = 1000; 10.000 ou 100.000

No primeiro caso, você obtém E = 2.7169239… . No segundo e = 2.7181459… e no terceiro está muito mais próximo do valor de e: 2.7182682. Já podemos parecer que com n = 1.000.000 ou maior, a abordagem será ainda melhor.

Em linguagem matemática, o procedimento de fazer n Ele fica mais perto e mais de um valor muito grande, é chamado limite para o infinito E é indicado assim:

Para denotar o infinito, o símbolo "∞" é usado.

O número e como uma soma

Também é possível definir o número E por meio desta operação:

Os números que aparecem no denominador: 1, 2, 6, 24, 120 ... correspondem à operação n!, onde:

n! = n. (N-1).(N-2). (N-3) ..

E por definição 0! = 1.

É fácil verificar se quanto mais adições são adicionadas, maior o número e.

Vamos fazer alguns testes com a calculadora, adicionando cada vez mais adições:

1 +1+ (1/2) + (1/6) = 2.71667

1 +1+ (1/2) + (1/6) + (1/24) = 2.75833

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806

Quanto mais termos eles são adicionados à soma, mais o resultado é semelhante a e.

Os matemáticos criaram uma notação compacta para essas somas que envolvem muitos termos, usando o símbolo da soma σ:

Esta expressão é lida como "soma de n = 0 para a infinidade de 1 entre n fatorial".

O número e do ponto de vista geométrico

O número E possui uma representação gráfica relacionada à área sob o gráfico da curva:

y = 1/x

Quando os valores de x estão entre 1 e E, esta área vale 1, conforme ilustrado na figura a seguir:

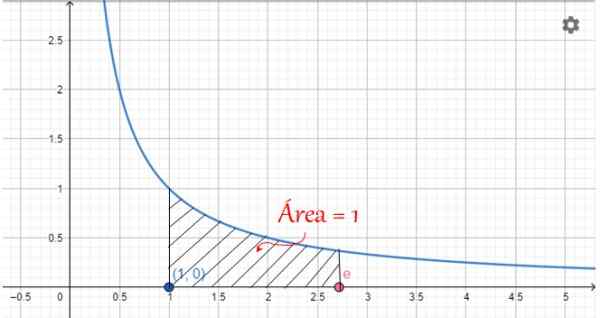Figura 2. Representação gráfica do número e: a área sob curva 1/x, entre x = 1 e x = e o'clock. Fonte: f. Zapata.

Propriedades Número E

Algumas das propriedades do número E são:

Pode atendê -lo: função crescente: como identificá -lo, exemplos, exercícios

-É irracional, em outras palavras, não pode ser obtido simplesmente dividindo dois números inteiros.

-O número e É também um Número transcendente, o que significa que e Não é uma solução de nenhuma equação polinomial.

-Está relacionado a outros quatro números famosos no campo da matemática, a saber: π, i, 1 e 0, através da identidade de Euler:

e^πi + 1 = 0

-As chamadas números complexos pode ser expresso através de E.

-Ele constitui a base dos logaritmos naturais ou neperianos hoje (a definição original de John Napier difere um pouco).

-É o único número que seu logaritmo neperiano vale 1, ou seja:

 ln e = 1

Formulários

Estatisticas

O número E aparece com muita frequência no campo de probabilidade e estatística, aparecendo em várias distribuições, como o normal ou gaussiano, o de Poisson e outros.

Engenharia

Na engenharia, é frequente, pois a função exponencial y = e^x Está presente em mecânica e eletromagnetismo, por exemplo. Entre as muitas aplicações que podemos citar:

-Um cabo ou corrente que fica sujeito às extremidades, adota a forma da curva dada por:

y = (e^x + e^-x) /2

-Um condensador C descarregou inicialmente, que se conecta em série a uma resistência r e uma fonte de tensão V para carregar, adquire uma certa carga q, dependendo do tempo t dado por:

Q (t) = CV (1-e^-T/rc)

biologia

A função exponencial y = a.e^Bx, Com a e B constante, é usado para modelar o crescimento celular e o crescimento bacteriano.

Físico

Na física nuclear, a decadência radioativa e a determinação das idades são modeladas por radiocarbono datado.

Economia

No cálculo do interesse composto, o número e surge naturalmente.

Suponha que você tenha uma certa quantia de dinheiro P_qualquer, para investir em uma taxa de juros anual.

Se o dinheiro for deixado por 1 ano, depois desse período você terá:

P (1 ano) = P_qualquer + P_qualquer.i = p_qualquer (1+ i)

Depois de mais um ano sem tocá -lo, você terá:

Pode servir a você: probabilidade teórica: como divulgá -lo, exemplos, exercícios

P (2 anos) = P_qualquer + P_qualquer.I + (P_qualquer + P_qualquer .i) i = p_qualquer +2 p_qualquer.I + p_qualquer.Yo²  = PO (1+i)²

E dessa maneira por n anos:

P = p_qualquer (1+i)ⁿ

Agora lembre -se de uma das definições de E:

Parece um pouco com a expressão para P, então deve haver um relacionamento.

Vamos distribuir a taxa de juros nominal Yo em n Períodos de tempo, dessa maneira, a taxa de juros composta será I/N:

P = p_qualquer [1+ (I/N)]ⁿ

Esta expressão parece um pouco mais sobre o nosso limite, mas ainda não é exatamente o mesmo.

No entanto, após algumas manipulações algébricas, pode -se mostrar que fazer essa mudança de variável:

h = n/i → i = n/h

Nosso dinheiro P se torna:

P = p_qualquer [1+ (1/h)]^oi = P_qualquer [1+ (1/h)]^hYo

E o que está entre as chaves, mesmo que seja escrito com a letra h, É igual ao argumento do limite que define o número e, perdendo apenas o limite.

Vamos fazer  h → ∞, e o que está entre as chaves é transformado no número e. Isso não significa que temos que esperar um grande momento infinitamente para retirar nosso dinheiro.

Se parecermos bem, ao fazer H = n/i E tendendo a ∞, o que realmente fizemos é distribuir a taxa de juros em períodos de tempo muito, muito pequenos: muito pequeno:

I = n/h

Isso é chamado Capitalização contínua. Nesse caso, a quantidade de dinheiro é facilmente calculada da seguinte forma:

P = p_qualquer .e^Yo

Onde eu é a taxa de juros anual. Por exemplo, depositando € 12 a 9 % ao ano, por meio de capitalização contínua, após um ano você tem:

P = 12 x e^{0.09 × 1} € = 13.€ 13

Com um ganho de 1.13 €.

Referências

1. Desfrute de matemática. Juros compostos: composição periódica. Recuperado de: desfrutar.com.
2. Figuera, j. 2000. Matemática 1ª. Diversificado. Edições Co-Bo.
3. Garcia, m. O número e no cálculo elementar. Recuperado de: matemática.Ciens.Ucv.ir.
4. Jiménez, r. 2008. Álgebra. Prentice Hall.
5. Larson, r. 2010. Cálculo de uma variável. 9NA. Edição. McGraw Hill.