Ângulos opostos pelo vértice (com um exercício resolvido)

O Ângulos opostos pelo vértice São aqueles que cumprem o seguinte: os lados de um deles são os prolongamentos dos lados do outro ângulo. Ele Teorema fundamental Dos ângulos opostos pelo vértice, diz: Dois ângulos opostos pelo vértice têm a mesma medida.

Muitas vezes o idioma é abusado dizendo que os ângulos opostos pelo vértice são os mesmos, o que não está correto. O fato de dois ângulos terem a mesma medida não significa que eles sejam iguais. É como dizer que duas crianças que têm a mesma altura são iguais.

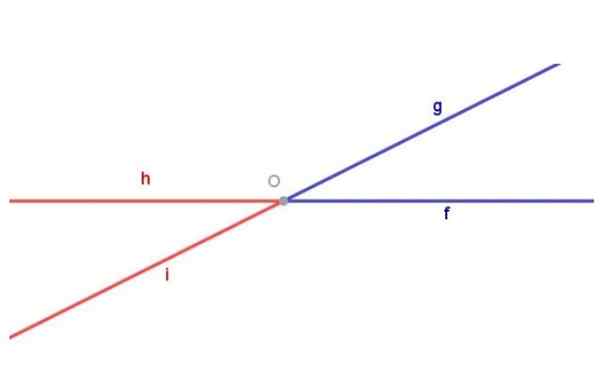
figura 1. Ângulos opostos pelo vértice. Preparado por: Fanny Zapata.

Lembre -se de que um ângulo é definido como a figura geométrica composta por duas semi -rigorosas com a mesma origem.

A Figura 1 mostra o ângulo NÉVOA (Azul) composto pelo semi -recreativo [De) e a semi -forte [OG) de origem comum QUALQUER. A Figura 1 também mostra o ângulo Hoi (vermelho) composto pelo semi -recreativo [Ouvi) e a semi -forte [OH) ambos com origem QUALQUER. 

Dois ângulos opostos pelo vértice são duas figuras geométricas diferentes. Para destacar isso, na Figura 1, o ângulo coloriu NÉVOA Azul, enquanto o ângulo Hoi Ele coloriu vermelho. 

Os ângulos azuis e vermelhos da Figura 1 são opostos pelo vértice porque: o semi -direito [De) do ângulo azul é o prolongamento do semi -direito [OH) do ângulo vermelho e o semi -direito [OG) do ângulo azul é o prolongamento do semi -direito [Ouvi) do ângulo vermelho.

[TOC]

Conceitos importantes sobre ângulos

Lados e vértices de um ângulo

A figura geométrica que consiste em duas semi -rigorosas com origem comum é um ângulo. A imagem a seguir mostra o ângulo POQ formado pelos dois semi -direito [Op) e [OQ) de origem comum QUALQUER:

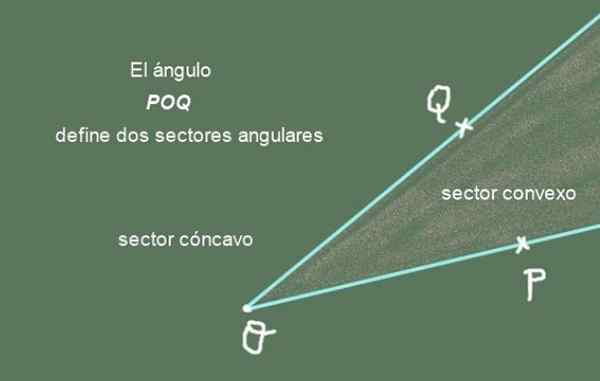Figura 2. O ângulo POQ define dois setores angulares. Preparado por: f. Zapata.

A semi -forte [Op) e [OQ) são os lados do ângulo POQ, enquanto o ponto comum ou é chamado Vértice do ângulo.

Pode atendê -lo: regra de ressecros

Setor angular: Um ângulo divide o plano que o contém em dois setores angulares. Um deles é o setor angular convexo e o outro é o setor angular côncavo. A união dos dois setores dá o avião completo.

A Figura 2 mostra no ângulo POQ e seus dois setores angulares. O setor angular convexo é aquele que tem uma forma pontiaguda, enquanto o côncavo é o setor angular do plano que falta o setor convexo.

Ângulos formados por duas linhas que são cortadas

Duas linhas de um plano que são interceptadas formam quatro ângulos e dividem o avião em quatro setores angulares.

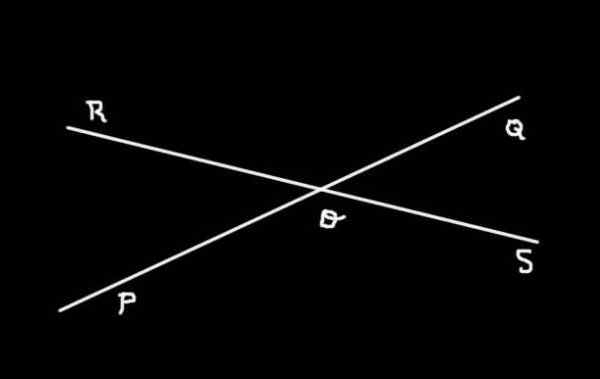Figura 3. As linhas (PQ) e (RS) são interceptadas em O e formam 4 ângulos. Preparado por: f. Zapata.

A Figura 3 mostra as duas linhas (PQ) e (RS) interceptado em QUALQUER. Lá você pode ver que quatro ângulos estão determinados:

-SOQ, Qor, ROP e POS

Os ângulos SOQ e Qor, Qor e ROP, ROP e POS, POS e SOQ são  ângulos adjacentes entre eles, enquanto SOQ e ROP Eles são opostos pelo vértice. Eles também são Ângulos opostos pelo vértice Os ângulos Qor e POS.

Linhas perpendiculares e ângulo reto

Duas linhas de secagem (linhas retas se cruzam) são Linhas retas perpendiculares Se eles determinam quatro setores angulares de igual medida. Se cada um dos quatro setores for simétrico com o setor angular adjacente, eles terão a mesma medida.

Cada um dos ângulos que determinam as duas linhas perpendiculares é chamado ângulo reto. Todos os ângulos retos têm a mesma medida.

Semi -Stramight na mesma linha e ângulo plano

Dada uma linha e um ponto, dois semi -rastreados são definidos. Esses dois semi -rastreados definem dois ângulos planos.

Na Figura 3, a linha pode ser observada (RS) e o ponto QUALQUER que pertence a (RS). O ângulo Sor É um ângulo plano. Também pode ser afirmado que o ângulo Ros É um ângulo plano. Todos os ângulos planos têm a mesma medida.

Pode atendê -lo: propriedade clausurativa

Ângulo nulo e ângulo total

Um único semi -recreativo define dois ângulos: um deles no setor angular convexo é o ângulo nulo E o outro, o do setor angular côncavo é o ângulo total. Na Figura 3 ângulo nulo SOS e ele ângulo total SOS. 

Medição 

Existem dois sistemas numéricos que são frequentemente usados ​​para dar a medição de um ângulo. 

Um deles é o sistema sexagesimal, ou seja, com base no número 60. É uma herança das culturas mesopotâmicas antigas. O sistema de medição de outros ângulos é o sistema Radián, com base no número π (PI) e é um legado dos sábios gregos antigos que desenvolveram geometria.

Sistema Sexagesimal

Ângulo nulo: No sistema sexagesimal, o ângulo nulo mede 0º (zero graus).

Ângulo total: A medida 360º é atribuída (trezentos e sessenta graus).

Ângulo plano: No sistema sexagesimal, o ângulo plano mede 180º (cento e oitenta graus).

Ângulo reto: Duas linhas perpendiculares dividem o plano em quatro ângulos de igual medida chamados ângulos retos. A medida de um ângulo reto é um quarto do ângulo total, ou seja, 90º (noventa graus).

Transportador ou goniômetro

O transportador é o instrumento usado para medir os ângulos. Consiste em um semicírculo (geralmente plástico transparente) dividido em 180 seções angulares. Como um semicírculo forma um ângulo plano, a medida entre duas seções consecutivas é 1º.

O goniômetro é semelhante ao transportador e consiste em um círculo dividido em 360 seções angulares.

Um ângulo cujos lados começam no centro do goniômetro interceptam dois setores e a medida desse ângulo em graus é igual ao número n de seções entre os dois setores interceptados, neste caso a medida será nº (lê ““ “ENEVERSOS”).

Pode atendê -lo: centímetros quadrados a metros quadrados (cm² a m²)

Teorema dos ângulos opostos pelo vértice

Formalmente, o teorema é declarado dessa maneira:

Se dois ângulos se opõem ao vértice, eles têm a mesma medida.

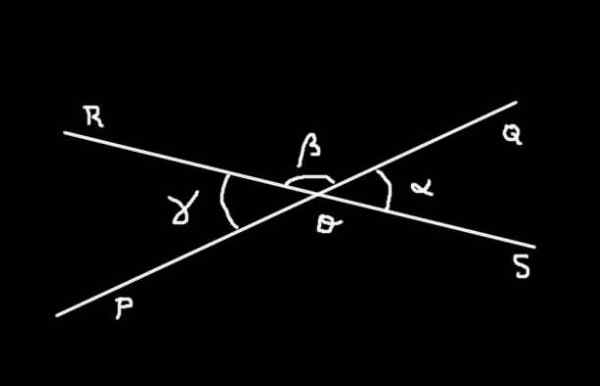Figura 4. α, β e γ são as medidas dos ângulos SOQ, Qor e ROP. Preparado por: f. Zapata.

Demonstração

O ângulo SOQ Tem medida α; o ângulo Qor Tem medida β e o ângulo ROP Tem γ medida. A soma do ângulo SOQ mais ele Qor formar o ângulo plano Sor da medida 180º.

Quer dizer que:

α + β = 180º

Por outro lado e usando o mesmo raciocínio com os ângulos Qor e ROP se tem:

β + γ = 180º

Se observarmos as duas equações anteriores, a única maneira que ambos são cumpridos é que α é igual a γ.

Como SOQ Tem medida α e é contestada pelo vértice a ROP da medida γ, e como α = γ, conclui -se que os ângulos opostos pelo vértice têm a mesma medida.

Exercício resolvido

Em referência à Figura 4: Suponha que β = 2 α. Encontre a medida dos ângulos SOQ, Qor e ROP Em graus sexagesimal.

Solução

Como a soma do ângulo SOQ mais ele Qor formar o ângulo plano Sor se tem:

α + β = 180º

Mas eles nos dizem que β = 2 α. Substituindo esse valor de β permanecemos:

α + 2 α = 180º

Quer dizer:

3 α = 180º

O que significa que α é a terceira parte de 180º:

α = (180º / 3) = 60º

Então a medida de SOQ é α = 60º. A medida de Qor é β = 2 α = 2*60º = 120º. Finalmente como ROP é oposto pelo vértice a SOQ Então, de acordo com o teorema, já demonstrou que eles têm a mesma medida. Isto é, a medida de ROP é γ = α = 60º. 

Referências

1. Baldor, J. PARA. 1973.Geometria plana e espacial. Cultural da América Central. 
2. Leis e fórmulas matemáticas. Sistemas de medição de ângulo. Recuperado de: IngeMecanica.com.
3. Wikipedia. Ângulos opostos pelo vértice. Recuperado de: é.Wikipedia.com
4. Wikipedia. Transportador. Recuperado de: é.Wikipedia.com
5. Zapata f. Goniômetro: história, peças, operação. Recuperado de: Lifer.com