Características, tipos e exemplos do movimento retilíneo

Ele movimento retilineal É aquele em que o celular se move ao longo de uma linha reta e, portanto, passa em uma dimensão, portanto também recebe o nome de Movimento unidimensional. Esta linha reta é a trajetória ou caminho seguido pelo objeto que se move. Os carros que viajam ao longo da avenida da Figura 1 seguem esse tipo de movimento.

Este é o modelo mais simples de movimento que pode ser imaginado. Os movimentos diários de pessoas, animais e coisas geralmente combinam transferências em linha reta com movimentos ao longo de curvas, mas alguns geralmente observam alguns que são exclusivamente retilíneos.

figura 1. Carros se movendo ao longo de uma avenida retilínea. Fonte: Pixabay.

Aqui estão alguns bons exemplos:

- Ao correr ao longo de uma pista retilínea de 200 metros.

- Dirigindo um carro em uma estrada reta.

- Soltar um objeto livremente de uma certa altura.

- Quando uma bola é jogada verticalmente.

https: // giphy.com/gifs/j5xx3bynaqv06wtoxq

Agora, o objetivo de descrever um movimento é alcançado especificando características como:

- Posição

- Deslocamento

- Velocidade

- Aceleração

- Tempo.

Para que um observador detecte o movimento de um objeto, é necessário ter um ponto de referência (origem o) e estabelecer um endereço específico para se mover, que pode ser o eixo x, O eixo e ou qualquer outro.

Quanto ao objeto que se move, isso pode ter inúmeras maneiras. Não há limitações a esse respeito, no entanto, em tudo o que se segue, será assumido que o celular é uma partícula; um objeto tão pequeno que suas dimensões não são relevantes.

Sabe -se que esse não é o caso de objetos macroscópicos; No entanto, é um modelo com bons resultados na descrição do movimento global de um objeto. Dessa forma, uma partícula pode ser um carro, um planeta, uma pessoa ou qualquer outro objeto que se mova.

Começaremos nosso estudo da cinemática retilínea com uma abordagem geral do movimento e, em seguida, casos específicos serão estudados como aqueles já nomeados.

[TOC]

Características gerais do movimento retilíneo

A descrição a seguir é geral e aplicável a qualquer tipo de movimento dimensional. A primeira coisa é escolher um sistema de referência. A linha ao longo da qual o movimento ocorre será o eixo x. Os parâmetros do movimento:

Posição

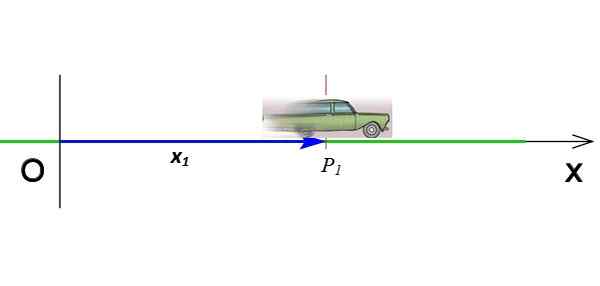Figura 2. Posição de um celular que se move no eixo x. Fonte: Wikimedia Commons (modificado por F. Zapata).

É o vetor que vai da origem até o ponto em que o objeto está em um instante dado. Na Figura 2, o vetor x₁ Indica a posição do celular quando está na coordenada P₁ e com o tempo t₁. As unidades vetoriais de posição no sistema internacional são metros.

Deslocamento

Deslocamento é o vetor que indica a mudança na posição. Na Figura 3, o carro passou da posição P₁ para a posição P₂, Portanto, seu deslocamento é δx = x₂ - x₁. Deslocamento é a subtração de dois vetores, é simbolizado com a letra grega δ ("delta") e, por sua vez, é um vetor. Suas unidades no sistema internacional são metros.

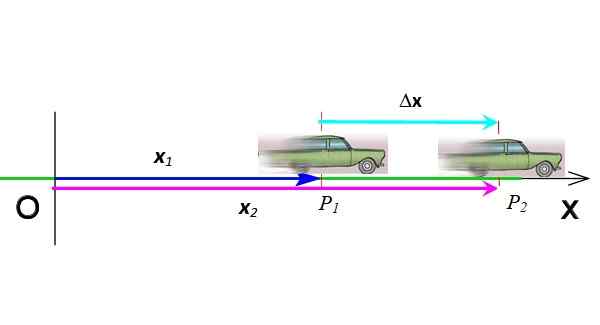Figura 3. Deslocamento vetorial. Fonte: preparado por f. Zapata.

Os vetores são indicados com ousado em texto impresso. Mas estar na mesma dimensão, se desejar, você pode fazer sem a notação vetorial.

Pode atendê -lo: ramos da física clássica e moderna

Distância percorrida

A distância d Visitou pelo objeto em movimento é o valor absoluto do vetor de deslocamento:

D = ΙxΙ = δx

Sendo um valor absoluto, a distância percorrida é sempre maior ou igual a 0 e suas unidades são as mesmas que as de posição e deslocamento. A notação de valor absoluto pode ser feita com barras de módulos ou simplesmente remover a letra em negrito no texto impresso.

Velocidade média

Quão rápido a posição muda? Existem telefones celulares lentos e rápidos. A chave sempre foi a velocidade. Para analisar esse fator, a posição é analisada x função do tempo t.

A velocidade média v_m (Veja a Figura 4) É a inclinação da linha de secagem (fúcsia) para a curva x vs t e fornece informações globais sobre deslocamento móvel no intervalo de tempo considerado.

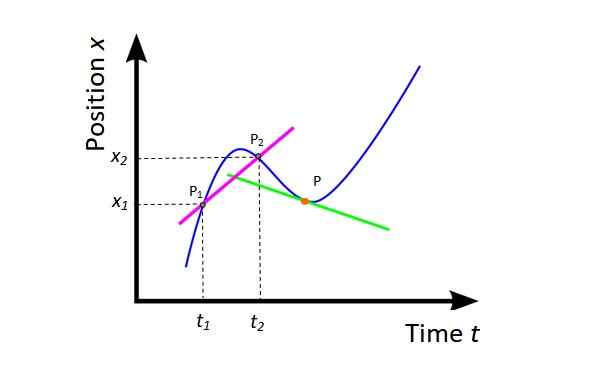Figura 4. Velocidade média e velocidade instantânea. Fonte: Wikimedia Commons, modificada por F. Zapata.

v_m = (x₂ - x₁) / (t₂ -t₁) = Δx / Δt

A velocidade média é um vetor cujas unidades no sistema internacional são medidores /segundo (EM).

Velocidade instantânea

A velocidade média é calculada tomando um intervalo de tempo mensurável, mas não informa sobre o que acontece dentro do referido intervalo. Para saber a velocidade a qualquer momento, você precisa fazer o intervalo de tempo muito pequeno, matematicamente, é equivalente a fazer:

ΔT → 0

A equação é dada anteriormente para velocidade média. Dessa maneira, a velocidade instantânea ou a velocidade é obtida:

Geometricamente, o derivado da posição em relação ao tempo é a inclinação da linha tangente à curva x vs t em um determinado ponto. Na Figura 4, o ponto é laranja e a linha tangente é verde. A velocidade instantânea neste ponto é a inclinação dessa linha.

Velocidade

A velocidade é definida como o valor absoluto ou o módulo de velocidade e é sempre positivo (sinalização, estradas e rodovias são sempre positivas, nunca negativas). Os termos "velocidade" e "velocidade" podem ser usados ​​diariamente, mas na física a distinção entre vetor e escalada é necessária.

v = ΙvΙ = v

Aceleração média e aceleração instantânea

A velocidade pode mudar no curso do movimento e a realidade é que ele deve fazê -lo. Há uma magnitude que quantifica essa mudança: aceleração. Se percebermos que a velocidade é a mudança de posição em relação ao tempo, a aceleração é a mudança de velocidade em relação ao tempo.

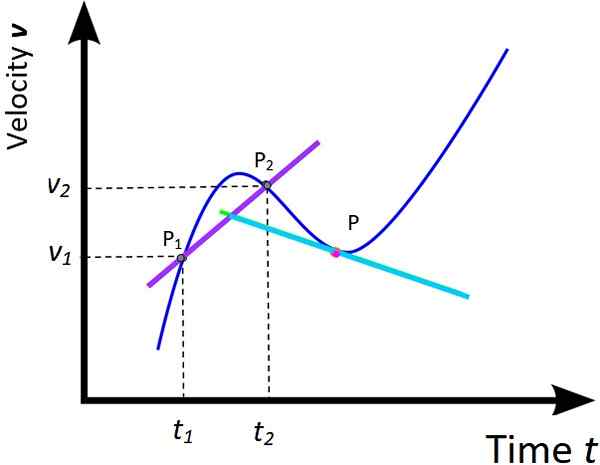Figura 5. Aceleração média e aceleração instantânea. Fonte: Wikimedia Commons, modificada por F. Zapata.

O tratamento dado ao gráfico de x vs t Das duas seções anteriores podem ser estendidas ao gráfico correspondente de v vs t. Consequentemente, uma aceleração média e aceleração instantânea são definidas como:

para_m = (v₂ - v₁) / (t₂ -t₁) = Δv / Δt  (Pendente da morada)

Aceleração e desaceleração

No movimento único -dimensional, os vetores por convenção têm sinais positivos ou negativos à medida que vão de uma maneira ou de outra. Quando a aceleração tem o mesmo significado que a velocidade, aumenta sua magnitude, mas quando faz o sentido oposto e a velocidade diminui sua magnitude. É dito então que o movimento está atrasado.

Pode servir a você: Leyden Bottle: Peças, Operação, Experiências

Pessoal

A classificação dos movimentos retilinês geralmente é feita com base em:

- Se a aceleração é ou não constante.

- O movimento passa ao longo de uma linha horizontal ou vertical.

Movimento com aceleração constante

https: // giphy.com/gifs/ylzfnbidhm7rp391fi

Quando a aceleração é constante, a aceleração média para_m É igual à aceleração instantânea para E há duas opções:

- Que a aceleração vale 0, nesse caso, a velocidade é constante e tem um movimento retilíneo uniforme ou mru.

- A aceleração constante diferente de 0, na qual a velocidade cresce ou diminui linearmente ao longo do tempo (o movimento retilíneo variou uniformemente ou MRUV):

Onde v_F  e t_F Eles são velocidade e tempo finais, respectivamente, e v_qualquer e t_qualquer Eles são velocidade e tempo iniciais. Sim t_qualquer = 0, Ao limpar a velocidade final, você já tem a equação familiar para a velocidade final:

v_F = v_qualquer + NO

Para este movimento, as seguintes equações também são válidas:

- Posição dependendo do tempo: x = x_qualquer + v_{qualquer .}T +½ em²

- Velocidade dependendo da posição: v_F² = v_qualquer² + 2º.Δx  (Com δx = x - x_qualquer)

Movimentos horizontais e movimentos verticais

Os movimentos horizontais são aqueles que passam ao longo do eixo horizontal ou do eixo x, enquanto os verticais o fazem ao longo do eixo e eixo. Os movimentos verticais sob a ação da gravidade são os mais frequentes e interessantes.

Nas equações anteriores, é tomado A = g = 9.8 m/s² direcionado verticalmente para baixo, a direção que quase sempre é escolhida com um sinal negativo.

Desta maneira, v_F = v_qualquer + NO Ele se transforma em v_F = v_qualquer - Gt E se a velocidade inicial for 0 porque o objeto foi retirado livremente, é ainda mais simplificado para v_F = - gt. Enquanto a resistência do ar não for levada em consideração, é claro.

Exemplos resolvidos

Exemplo 1

No ponto, um pequeno pacote é liberado para que esteja se movendo ao longo do transportador com rodas deslizantes ABCD mostradas na figura. Enquanto desce pelas seções inclinadas AB e CD, o pacote carrega uma aceleração de 4,8 m/s², Enquanto na seção horizontal BC mantém velocidade constante.

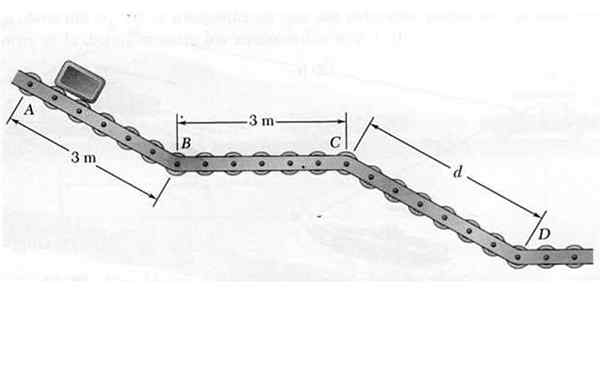Figura 6. O pacote que se move no caminho deslizante do Exemplo Solvido 1. Fonte: Self feito.

Sabendo que a velocidade com que o pacote em d é de 7,2 m/s, determine:

a) A distância entre C e D.

b) O tempo necessário para o pacote chegar ao fim.

Solução

O movimento do pacote é realizado nas três seções retilíneas mostradas e para calcular o solicitado, a velocidade é necessária nos pontos B, C e D. Vamos analisar cada seção separadamente:

Seção AB

Como o tempo não está disponível nesta seção, ele será usado v_F² = v_qualquer² + 2º.Δx  Com vo = 0:

v_F² = 2a.Δx → v_F²= 2. 4,8 m/s² . 3 m = 28.8 m²/s² → v_F  = 5.37 m/s = V_B

O tempo que o pacote leva para viajar a seção AB é:

t_Ab = (v_F - v_qualquer) /A = 5.37 m/s/4,8 m/s² = 1.19 s

Seção BC

A velocidade na seção BC é constante, portanto v_B = v_C = 5.37 m/s. O tempo que leva para o pacote viajar nesta seção é:

Pode servir a você: refração leve: elementos, leis e experimentos

t_Bc = distância _Bc  / v_B = 3 m/ 5.37 m/s = 0.56 s

Seção de CD

A velocidade inicial desta seção é v_C = 5.37 m/s, A velocidade final é v_D = 7,2 m/s, via v_D²  = v_C² + 2. para. d O valor de d:

D = (v_D²  - v_C²)/2.a = (7.2²  - 5.37²)/2 x 4.8 m = 2.4 m

O tempo é calculado como:

t_{CD =} (v_D  - v_C)/A = (7.2-5.37)/ 4.8 s = 0.38 s.

As respostas para as perguntas levantadas são:

a) d = 2.4 m

b) O tempo de viagem é t_Ab + t_Bc + t_CD = 1.19 s +0.56 S +0.38 s = 2.13 s.

Exemplo 2

Uma pessoa está sob um portão horizontal que é inicialmente aberto e 12 m de altura. A pessoa lança verticalmente um objeto em direção ao portão com velocidade de 15 m/s.

Sabe -se que o portão fecha 1,5 segundos depois que a pessoa lançou o objeto a partir de uma altura de 2 metros. A resistência do ar não será levada em consideração. Responda às seguintes perguntas, justificando:

a) Você consegue passar o objeto pelo portão antes de fechar?

b) O objeto sempre colidirá contra o portão fechado? Se afirmativo, quando isso acontece?

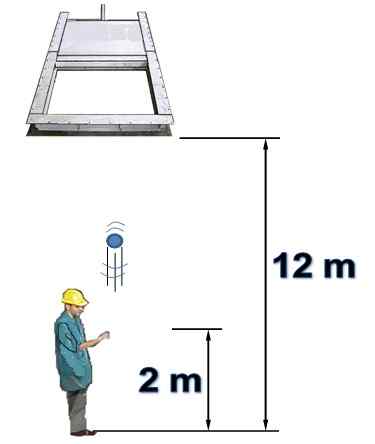Figura 7. Um objeto é lançado verticalmente (Exemplo 2 resolvido). Fonte: Self feito.

Responda para)

Existem 10 metros entre a posição inicial da bola e o portão. É um lançamento vertical, no qual este endereço é considerado positivo.

Você pode descobrir a velocidade que ele carrega quando chegar a esse ponto, com este resultado o tempo necessário para fazê -lo e compará -lo com o tempo de fechamento do portão, que é 1.5 segundos:

v_F ²= v_qualquer ²- 2.g. Δe → v_F = (15² - 2 x 9.8 x10)^1/2 M = 5.39 m/s

T = (V_F - v_qualquer) /g = (5.39 - 15) / (-9.8) s = 0.98 s

Como desta vez é menor que 1.5 segundos, conclui -se que o objeto pode passar pelo portão pelo menos uma vez.

Resposta b)

Já sabemos que o objeto gerencia. A velocidade, quando atinge o auge do portão, tem a mesma magnitude que quando ele sobe, mas na direção oposta. Portanto, trabalhe com -5.39 m/se o tempo necessário para alcançar esta situação é:

T = (V_F - v_qualquer) /G = (-5.39 - 15) / (-9.8) S = 2.08 s

Como o portão permanece aberto apenas para 1.5 s, é evidente que não tem tempo de passar antes de fechar, pois encontra. A resposta é: o objeto se colidir com o portão fechado após 2.08 segundos após ser lançado, quando está descendente.

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).69-116.
2. Giancoli, d. Física. (2006). Princípios com aplicações. 6^º Edição. Prentice Hall. 22-25.
3. Kirkpatrick, l. 2007. Física: uma olhada no mundo. 6^ta Edição abreviada. Cengage Learning. 23 - 27.
4. Resnick, r. (1999). Físico. Volume 1. Terceira edição em espanhol. México. Empresa Editorial Continental S.PARA. claro.V. 21-22.
5. Rex, a. (2011). Fundamentos da Física. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14^º. Ed. Volume 1. 50 - 53.
7. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7^MA. Edição. México. Editores de aprendizado do Cengage. 23-25.
8. Serway, r., Vulle, c. (2011). Fundamentos da Física. 9^{n / D} Ed. Cengage Learning. 43 - 55.
9. Wilson, J. (2011). Física 10. Pearson Education. 133 - 149.