Momento de fórmulas de inércia, equações e exemplos de cálculo

Ele momento de inércia De um corpo rígido em relação a um certo eixo de rotação, representa sua resistência a mudar sua velocidade angular em torno desse eixo. É proporcional à massa e também à localização do eixo de rotação, uma vez que o corpo, de acordo com sua geometria, pode girar mais facilmente em torno de certos eixos do que em outros.

Suponha que um objeto extenso (consistindo de muitas partículas) que possa girar em torno de um eixo. Suponha que um força age F, aplicado tangencialmente ao elemento de massa Δm_Yo, que produz um torque ou momento, dado por τ_líquido = ∑r_Yo x F_Yo. O vetor r_Yo É a posição de Δm_Yo (Veja a Figura 2).

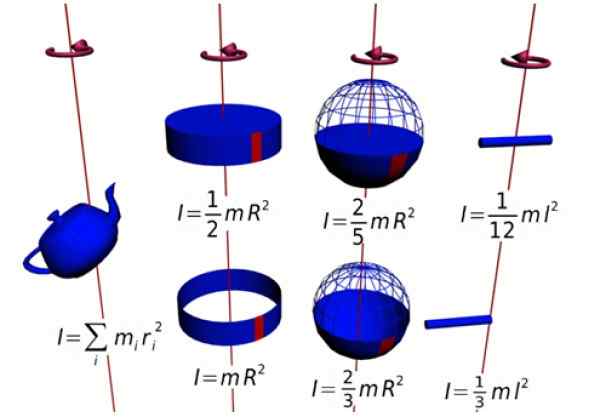
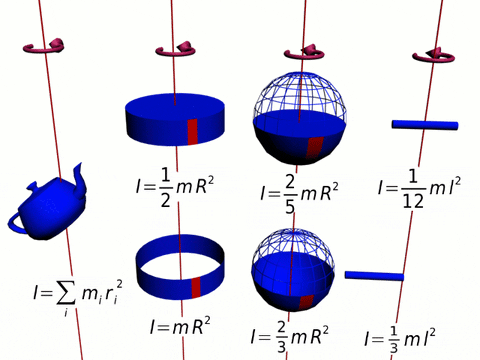figura 1. Momentos de inércia de várias figuras. Fonte: Wikimedia Commons.

Este momento é perpendicular ao plano de rotação (endereço +K = deixando papel). Como a força e a posição radial são sempre perpendiculares, o produto cruzado permanece:

τ_líquido = ∑ f_Yo r_Yo k = ∑ (ΔM_Yo para_Yo) r_Yo  k = ∑ ΔM_Yo (para_Yo r_Yo ) k

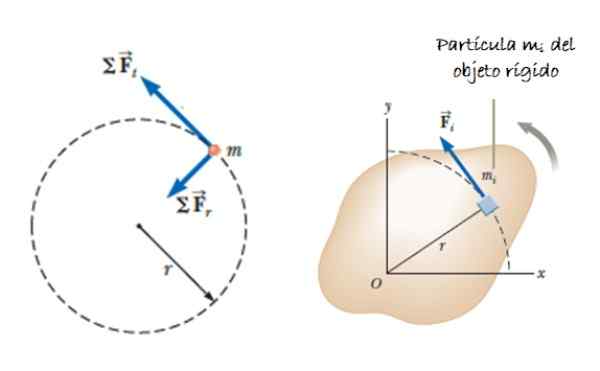Figura 2. Uma partícula pertencente a um sólido rígido em rotação. Fonte: Serway, r. 2018. Física para Ciência e Engenharia. Volume 1. Cengage Learning.

Aceleração a_Yo representa o componente tangencial da aceleração, uma vez que a aceleração radial não contribui para o torque. Dependendo da aceleração angular α, podemos indicar que:

para_Yo = α r_Yo

Portanto, o torque líquido é assim:

τ_líquido = ∑ ΔM_Yo (α r_Yo²) K = (∑ r_Yo² Δm_Yo) α k

A aceleração angular α é a mesma para todo o objeto; portanto, não é afetado pelo subscrito "i" e pode deixar a soma, que é precisamente o momento de inércia do objeto simbolizado com a letra I:

I = ∑ r_Yo² Δm_Yo

Este é o momento de inércia de uma distribuição de massa discreta. Quando a distribuição é contínua, a soma é substituída por uma integral e Δm se torna um diferencial em massa Dm. A integral é feita acima de tudo o objeto:

I = ∫_M(r²) Dm

As unidades do momento da inércia no sistema internacional se forem kg x m². É uma quantidade escalar e positiva, pois é o produto de uma massa pelo quadrado de uma distância.

[TOC]

Exemplos de cálculo

Um objeto estendido, como uma barra, disco, esfera ou outro, cuja densidade ρ É constante e saber que a densidade é o quociente de massa - volume, o diferencial de massa Dm Está escrito como:

ρ = dm/dv → dm = ρDv

Substituindo na integral para o momento da inércia, temos:

I = ∫r² ρdv = ρ ∫r²Dv

Esta é uma expressão geral, válida para um objeto tridimensional, cujo volume V e posição r São funções de coordenadas espaciais x, e e z. Observe que, sendo constante, a densidade está fora da integral.

A densidade ρ Também é conhecido como densidade volumétrica, mas se o objeto for muito plano, como uma folha ou muito fina e estreita como uma haste, outras formas de densidade podem ser usadas, vamos ver:

Pode atendê -lo: movimento de rotação da terra

- Para uma folha muito fina, a densidade a ser usada é σ, a densidade da superfície (massa por unidade de área) e dá é o diferencial de área.

- E se for uma barra fina, onde apenas o comprimento é relevante, a densidade de massa linear é usada λ e um diferencial de comprimento, de acordo com o eixo usado como referência.

Nos exemplos a seguir, todos os objetos são considerados rígidos (não -deformáveis) e têm densidade uniforme.

Momento de inércia de uma barra fina em relação a um eixo que passa pelo seu centro

Aqui vamos calcular o momento de inércia de uma barra fina, rígida e homogênea, de comprimento l e massa m, com relação a um eixo que passa pelos meios.

Em primeiro lugar, é necessário estabelecer um sistema de coordenadas e construir uma figura com geometria adequada, como esta:

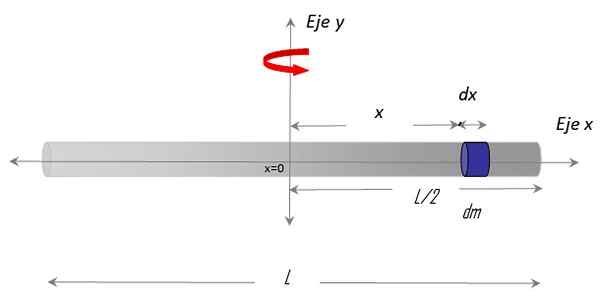Figura 3. Geometria para calcular o momento de inércia de uma haste fina em relação a um eixo vertical que passa pelo seu centro. Fonte: f. Zapata.

Ele foi escolhido X eixo ao longo da barra e o Eixo y como eixo de rotação. O procedimento para estabelecer integral também exige a escolha de um diferencial em massa no bar, chamado Dm, que tem um comprimento diferencial Dx e está localizado na posição x arbitrário, com relação ao centro x = 0.

De acordo com a definição de densidade de massa linear λ:

λ = m/l

Quando a densidade é uniforme, que é válida para M e L, é também para DM e DX:

λ = dm/dx → dm = λdx.

Por outro lado, o elemento de massa está em posição x, Então, substituindo essa geometria na definição, temos uma integral definida, cujos limites são os extremos da barra de acordo com o sistema de coordenadas:

Substituindo a densidade linear λ = m/l:

Para encontrar o momento de inércia da barra em relação a outro eixo de rotação, por exemplo, um que passa por uma de suas extremidades, você pode usar o teorema de Steiner (consulte o exercício resolvido no final) ou realizar um cálculo direto semelhante ao que mostrado aqui, mas modificando adequadamente a geometria.

Momento de inércia de um álbum em relação a um eixo que passa pelo seu centro

Um álbum muito fino, de espessura desprezível é uma figura plana. Se a massa for distribuída uniformemente em toda a área A, a densidade de massa σ é:

σ = M/a

Muito Dm como dá corresponde à massa e à área do anel diferencial mostrado na figura. Assumiremos que todo o conjunto gira em torno do eixo e.

Você pode imaginar que o álbum é composto que muitos anéis concêntricos de rádio r, cada um com seu respectivo momento de inércia. Adicionando as contribuições de todos os anéis até chegar ao rádio R, Você terá a inércia total do álbum.

σ = dm/da → dm = σdá

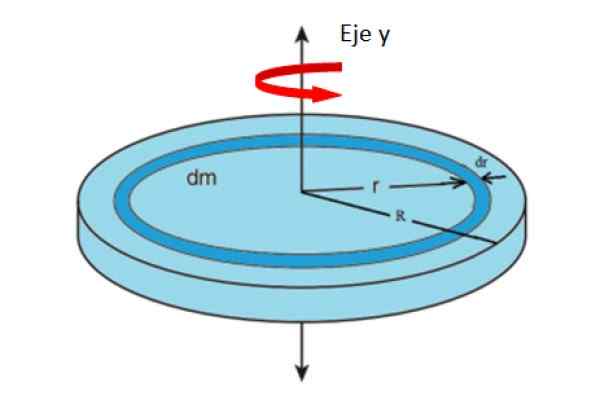Figura 4. Geometria para calcular o momento de inércia de um álbum, com relação ao eixo axial. Fonte: f. Zapata.

Onde m representa toda a massa do álbum. A área de um álbum depende de seu raio r como:

Pode atendê -lo: velocidade de propagação de uma onda

A = π.r²

Derivando sobre r:

Da /dr = 2 = 2π.R → da = 2π.rdr

Substituindo o acima na definição de i:

Depois de avaliar os resultados integrais:

Substituindo σ = m/(π.R² ) é deixado:

Momento de inércia de uma esfera sólida em relação a um diâmetro

Uma esfera Radius R pode ser considerada como uma série de discos empilhados um no outro, onde cada álbum de massa infinitesimal Dm, rádio r e espessura Dz, Tem um momento de inércia dada por:

deu_disco = (½) r²Dm

Para encontrar esse diferencial, a fórmula da seção anterior foi simplesmente tomada e substituída M e R por Dm e r, respectivamente. Um álbum como esse pode ser visto na geometria da Figura 5.

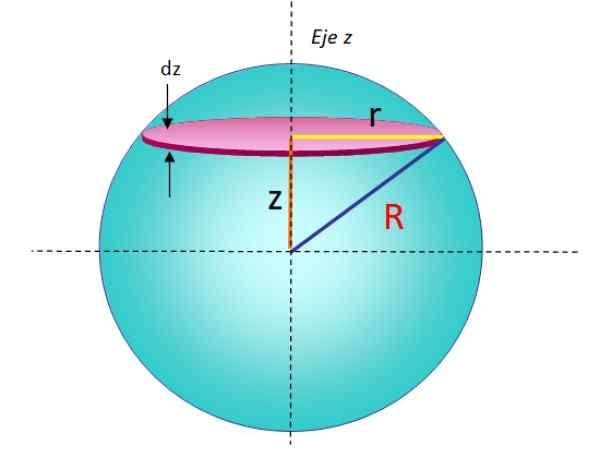Figura 5. Geometria para calcular o momento de inércia de uma esfera de raio sólido em relação a um eixo que passa por um diâmetro. Fonte: f. Zapata.

Ao adicionar todos os momentos de inércia infinitesimal de discos empilhados, é obtido o momento de inércia total da esfera:

Yo_esfera = ∫di_disco

Que é equivalente a:

I = ∫_esfera (½) r²Dm

Para resolver a integral, você precisa expressar Dm apropriadamente. Como sempre, é alcançado a partir da densidade:

ρ = m/v = dm/dv → dm = ρ.Dv

O volume de um disco diferencial é:

Dv = área base x altura

A altura do álbum é a espessura Dz, Enquanto a área base é πr², portanto:

Dv = πr²Dz

E substituir no integrado seria assim:

I = ∫_esfera(½) r²Dm = ∫ (½) r²(ρπr²Dz)

Mas antes de integrar, deve. Através do teorema de Pitágoras:

R² = r² + z² → R² = R² - z²

 Isso nos leva a:

I = ∫_esfera(½) ρ r²(πr²dz) = ∫_esfera(½) ρ π r⁴Dz= ∫_esfera(½) ρ π (r² - z²)² Dz

Para integrar toda a esfera, notamos que Z varia entre -r e r, portanto:

Sabendo que ρ = m/v = m/[(4/3) πr³] Finalmente, é obtido, depois de simplificar:

Momento de inércia de um cilindro sólido em relação ao eixo axial

Para este objeto, um método semelhante ao usado para a esfera é usado, só que desta vez é mais fácil se o cilindro for imaginado para conchas de rádio cilíndricas r, grossura Dr e altura H, Como se fossem as camadas de uma cebola.

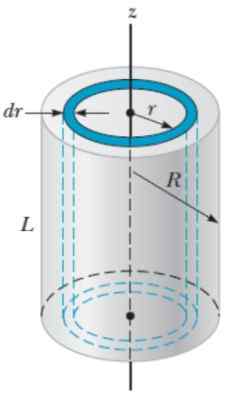Figura 6. Geometria para calcular o momento de inércia de um raio sólido RAIU CILIND. Fonte: Serway, r. 2018. Física para Ciência e Engenharia. Volume 1. Cengage.

O volume Dv de uma camada cilíndrica é:

Dv = 2π.Rl.Dr

Portanto, a massa de Cascaron é:

Pode servir a você: Escala Microscópica: Propriedades, Conde Partículas, Exemplos

Dm = ρ.Dv = ρ. 2π.r.eu.Dr

Esta expressão é substituída na definição de momento de inércia:

 Já que ρ = m / (π.R²EU) é sobrou:

A equação anterior indica que o momento de inércia do cilindro não depende de seu comprimento, mas de sua massa e apenas seu raio. Sim eu mudou, o momento da inércia em relação ao eixo axial continuaria sendo o mesmo. Por esta razão, Yo do cilindro coincide com o do álbum fino calculado anteriormente.

Momento de inércia de uma folha retangular em relação a um eixo que passa pelo seu centro

O Eixo y Horizontal como eixo de rotação. A figura abaixo mostra a geometria necessária para realizar integração:

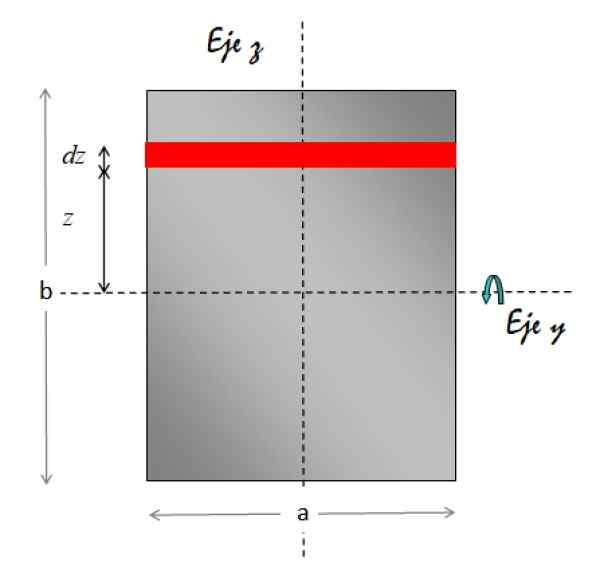Figura 7. Geometria para o cálculo do momento de inércia de uma placa retangular em relação a um eixo paralelo para a folha e que passa pelo seu centro. Fonte: f. Zapata.

O elemento de área indicado em vermelho é retangular. Sua área é base x altura, portanto:

da = a.Dz

Portanto, o diferencial de massa é:

Dm = σ.da = σ.(para.Dz)

Quanto à distância do elemento de área do eixo de rotação, é sempre z. Substituímos tudo isso na integral do momento da inércia:

Agora a densidade de massa da superfície σ é substituída por:

σ = m/ab

E é definitivamente assim:

Observe que é como o da barra fina.

Momento de inércia de uma folha quadrada em relação a um eixo que passa pelo seu centro

Para um quadrado ao lado eu, Na expressão anterior válida para um retângulo, o valor de b por um eu:

Teoremas do momento da inércia

Existem dois teoremas especialmente úteis para simplificar o cálculo de momentos de inércia em relação a outros eixos, que de outra forma poderiam ser complicados de encontrar para a falta de simetria. Esses teoremas são:

Teorema de Steiner

Também chamado Teorema do eixo paralelo, relaciona o momento da inércia em relação a um eixo com outro que passa pelo centro de massa do objeto, desde que os eixos sejam paralelos. Para aplicá -lo, a distância d precisa ser conhecida entre os dois eixos e, claro, a massa m do objeto.

Ser Yo_z o momento de inércia de um objeto estendido em relação a Z, eu eixo_Cm O momento da inércia em relação a um eixo que passa pelo centro de massa (CM) do referido objeto, então é cumprido que:

Yo_z = I_Cm + MD²

Ou na notação da figura a seguir: Yo_{z '} = I_z + MD²

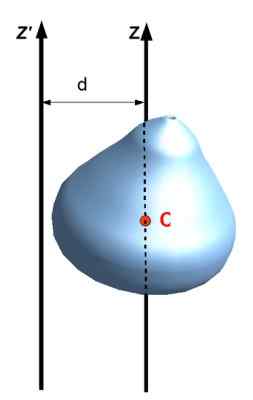Figura 8. Teorema de Steiner ou eixos paralelos. Fonte: Wikimedia Commons. Jack See [CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0)]

Teorema do eixo perpendicular

Este teorema se aplica a superfícies planas e diz: o momento de inércia de um objeto plano em torno de um eixo perpendicular a ele é a soma dos momentos de inércia em torno de dois eixos perpendiculares ao primeiro eixo:

Yo_z = I_x + Yo_e

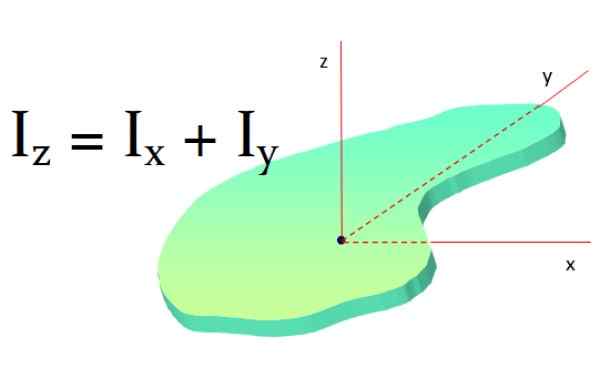Figura 9. Teorema do eixo perpendicular. Fonte: f. Zapata.

Se o objeto tiver simetria de tal forma que Yo_x e Yo_e Eles são iguais, então é cumprido que:

Yo_z = 2i_x

Exercício resolvido

Encontre o momento de inércia da barra em relação a um eixo que passa por uma de suas extremidades, como a mostrada na Figura 1 (abaixo e à direita) e Figura 10.

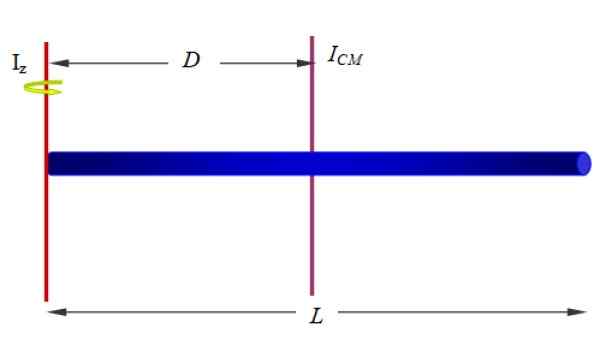Figura 10. Momento de inércia de uma barra homogênea em torno de um eixo que passa por uma extremidade. Fonte: f. Zapata.

Solução:

Já temos o momento de inércia do bar em torno de um eixo que passa por seu centro geométrico. Como o bar é homogêneo, seu centro de massa é nesse ponto, então este será nosso Yo_Cm Para aplicar o teorema de Steiner.

Se o comprimento da barra for eu, O eixo z está a uma distância d = l/2, portanto:

Yo_z = I_Cm + MD²= (1/12) ml²+M (l/2)²= (1/3) ml²

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill. 313-340
2. Rex, a. 2011. Fundamentos da Física. Pearson. 190-200.
3. Teorema do eixo paralelo. Recuperado de: hiperfísica.Phy-Atr.GSU.Edu.
4. Serway, r. 2018. Física para Ciência e Engenharia. Volume 1. Cengage.
5. Universidade Sevilla. Momento de inércia de sólidos esféricos. Recuperado de: Laplace.nós.é.
6. Universidade Sevilla. Momento de inércia de um sistema de partículas. Recuperado de: Laplace.nós.é.
7. Wikipedia. Teorema do eixo paralelo. Recuperado de: em.Wikipedia.org