Sanduíche Explicação e Exercícios

O Lei de Sanduíche ou tortilha é um método que permite operar com frações; Especificamente, ele permite dividir frações. Em outras palavras, através desta lei, você pode fazer divisões de números racionais. A lei de Sandwich é uma ferramenta útil e simples para lembrar.

Este artigo será considerado apenas o caso de divisão de números racionais que não são números inteiros. Esses números racionais também são conhecidos como números fracionários ou quebrados.

Explicação

Suponha que você precise dividir dois números fracionários a/b ÷ c/d. A lei de sanduíche consiste em expressar esta divisão da seguinte maneira:

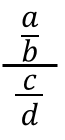
Esta lei estabelece que o resultado é obtido multiplicando o número localizado na extremidade superior (neste caso, o número "A") pelo número de extremidade inferior (neste caso "D") e dividindo essa multiplicação entre o produto do produto do números médios (neste caso, "B" e "C"). Assim, a divisão anterior é igual a × d/b × c.

Pode ser observado na maneira de expressar a divisão anterior que a linha média é mais longa que a dos números fracionários. Também é apreciado que é semelhante a um sanduíche, já que as tapas são os números fracionários que você deseja dividir.

Essa técnica de divisão também é conhecida como C duplo, pois um grande "C" pode ser usado para identificar o produto de números extremos e um "C" menor para identificar o produto dos números médios:

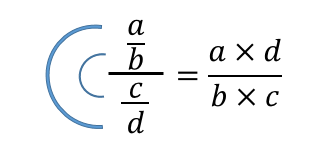
Ilustração

Números fracionários ou racionais são números da forma m/n, onde "m" e "n" são números inteiros. O inverso multiplicativo de um número racional m/n consiste em outro número racional que, multiplicando -o por m/n, resulta no número um (1).

Este inverso multiplicativo é indicado por (m/n)^-1 E é igual a n/m, já que m/n × n/m = m × n/n × m = 1. Por notação, você também precisa (m/n)^-1= 1/(m/n).

A justificativa matemática da Lei de Sandwich, bem como outras técnicas existentes para dividir frações, reside no fato de que, dividindo dois números racionais A/B e C/D, no fundo o que está sendo feito é a multiplicação de A/B Para o inverso multiplicativo de C/D. Isto é:

A/b ÷ c/d = a/b × 1/(c/d) = a/b × (c/d)^-1= a/b × d/c = a × d/b × c, como obtido anteriormente.

Para não funcionar mais, algo que deve ser levado em consideração antes de usar a lei do sanduíche é que ambas as frações são o mais simplificadas possível, pois há casos em que não é necessário usar a lei.

Por exemplo, 8/2 ÷ 16/4 = 4 ÷ 4 = 1. A lei do sanduíche poderia ter sido usada, obtendo o mesmo resultado após simplificar.

Outra coisa importante a considerar é que essa lei também pode ser usada quando um número fracionário é exigido por um número inteiro. Nesse caso, um 1 deve ser colocado sob o número inteiro e passar a usar a lei do sanduíche como antes. Isso ocorre porque qualquer número inteiro K cumpre que k = k/1.

Exercícios

Abaixo está uma série de divisões nas quais a lei do sanduíche é usada:

• 2 ÷ (7/3) = (2/1) ÷ (7/3) = (2 × 3)/(1 × 7) = 6/7.
• 2/4 ÷ 5/6 = 1/2 ÷ 5/6 = 1 × 6/2 × 5 = 6/10 = 3/5.

Nesse caso, as frações 2/4 e 6/10 foram simplificadas, dividindo entre 2 para cima e para baixo. Este é um método clássico para simplificar as frações que consistem em encontrar os divisores comuns do numerador e do denominador (se houver) e dividir ambos entre o divisor comum até que uma fração irredutível seja obtida (na qual não há divisores comuns).

• (xy+y)/z ÷ (x+1)/z²= (xy+y) z²/z (x+1) = (x+1) yz²/z (x+1) = yz.

Referências

1. Almaguer, g. (2002). Matemática 1. Limusa editorial.
2. Álvarez, J., Jácome, J., López, J., Cruz, e. d., & Tetumo, j. (2007). Matemática básica, elementos de suporte. Univ. J. Autônomo de Tabasco.
3. Bails, b. (1839). Princípios da aritmética. Impresso por Ignacio cumprido.
4. Barker, l. (2011). Textos nivelados para matemática: número e operações. Materiais criados pelo professor.
5. Barrios, a. PARA. (2001). Matemática 2ª. Editorial Progreso.
6. Eguiluz, m. eu. (2000). Frações: uma dor de cabeça? Novos livros.