Sinais de lei

Explicamos a lei dos sinais, com exemplos e exercícios resolvidos

Esquema da Lei dos Sinais

Qual é a lei dos sinais?

O Sinais de lei É o conjunto de regras usadas em cálculos aritméticos e algébricos com números reais para atribuir corretamente o sinal ao resultado, quando quantidades positivas e negativas estão envolvidas.

Existem regras adequadas de acordo com a operação realizada: soma, subtração, multiplicação e divisão, que são as mais básicas, e também existem regras de sinais relacionados às operações de potencialização e arquivamento.

Em uma determinada operação, seja manual ou com calculadora, é necessário aplicar corretamente a lei dos sinais para garantir um resultado correto, pois apenas uma pequena alteração nos sinais altera significativamente os valores.

A lei dos sinais para cada operação aritmética básica e os casos que podem surgir são examinados abaixo.

Lei dos sinais em soma

1) Se os números a serem adicionados têm o mesmo sinal

Os números são adicionados como de costume e o resultado é adicionado ao sinal dos números, independentemente de ser positivo ou negativo.

É importante ter em mente que números positivos geralmente não estão antes do sinal, mas são escritos diretamente. Por outro lado, números negativos são escritos entre parênteses, especialmente quando são precedidos pelo símbolo de uma operação aritmética, a fim de evitar confusão.

Exemplos de somas de números com o mesmo sinal:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21

2) Se os números a serem adicionados tiverem sinal diferente

Os números são subtraídos e o sinal do número que tem o maior valor absoluto é agregado ao resultado, positivo ou negativo.

Como exemplo, execute a operação 5 + (−14). Como o valor absoluto de (-14) é maior que o valor absoluto de 5, 5 unidades são subtraídas de 14, o que fornece 9 e esse resultado é colocado sinal negativo:

Pode atendê -lo: prismas e pirâmides

5 + (−14) = −9

Mais exemplos dessa regra aplicados à soma de dois números de sinais diferentes são:

(−27) + 12 = −15

12 + (−7) = 5

Se na operação houver mais de duas adições com sinais diferentes, o propriedade associativa da soma:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

A operação é realizada pela primeira vez no pracete, que consiste na soma de dois números de sinal diferente, para o qual a regra descrita é aplicada: o resultado é subtraído e o sinal do número com o maior valor absoluto:

(−20) + 9 = −11

A operação é assim:

(−20) + 9 + (−7) = (−11) + (−7)

Agora você tem a soma de dois números do mesmo sinal, eles são normalmente adicionados e o resultado é colocado um sinal negativo:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Sinais no substituto

A subtração de dois números é definida como a soma do oposto. Por sua vez, o oposto de um número é dito número com o sinal alterado. Por exemplo, o oposto de 2 é (-2), o oposto de (-5) é 5 e assim por diante.

Com isso em mente, quando você tem a subtração de dois números:

A - b

Simplesmente se transforma na soma do oposto de B:

A + ( - b)

E prossiga conforme descrito na seção anterior. Nota para colocar um sinal + um número negativo não o altera, mas muito cuidadoso, o oposto não é verdadeiro.

Quando o número "A", que é o minuenda, é maior que o número "B", que é roubado, opera como na subtração de números naturais. Não há problema, já que um grande número está sendo subtraído de uma quantidade menor:

Pode atendê -lo: desigualdade do triângulo: demonstração, exemplos, exercícios resolvidos

25 - 8 = 17

Com os exemplos a seguir, o método de adicionar o oposto de subtrair é muito conveniente:

(−5) - 24 = (−5) +( - 24) = - 29
32 - (−23) = 32 + 23 = 55

Lei dos Sinais de Multiplicação

A lei dos sinais de multiplicação é aplicada dessa maneira:

• Ao multiplicar dois números do mesmo sinal, o resultado é sempre positivo.
• O produto de dois números de sinal oposto é sempre negativo.

O resumo da regra de sinais para multiplicação é mostrado na imagem:

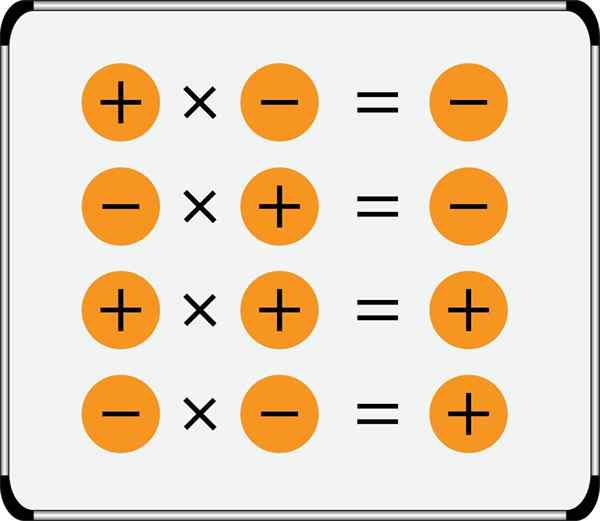
Observe que números positivos podem ser escritos sem o sinal anterior, mas os números negativos sempre o têm, além disso, dois símbolos aritméticos nunca são escritos um para o outro, eles sempre devem ser separados por um parêntese, por exemplo:

Incorreta: 3 × −4
Correto: 3 × (−4) = −12

(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

Para multiplicar mais de dois números, a propriedade associativa da multiplicação é usada, pois a ordem dos fatores não altera o produto, por exemplo, ao realizar:

(−2) × (−14) × 16

Você pode multiplicar os dois primeiros fatores, ou os dois últimos, se quiser, e depois multiplicar o resultado pelo fator restante. Nesse caso, os dois fatores serão multiplicados primeiro a partir da esquerda:

[(−2) × (−14)] × 16

O produto de dois números negativos é positivo, então (-2) × (-14) = 28 e permanece:

28 × 16 = 448

Lei dos Sinais de Divisão

É análogo à regra dos sinais de multiplicação:

• A proporção de dois números do mesmo sinal é sempre positiva.
• Ao dividir dois números de sinal, o resultado é sempre negativo.

Pode atendê -lo: diferença entre círculo e circunferência (com exemplos)

Por exemplo:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36

Lei dos sinais de empoderamento e arquivamento

Um expoente de número por escrito é:

paraⁿ

Onde "a" é a base e "n" é o expoente. Dois casos são distinguidos, de acordo com a paridade do expoente:

Caso 1: A é positivo

Quando a base é positiva, o resultado é positivo, independentemente de o expoente ser par ou estranho, como em:

2³ = 8
3⁴ = 81

Caso 2: A é negativo

Aqui estão dois casos:

• Quando o expoente é par, então o resultado é positivo.
• Se o expoente for estranho, é negativo.

Exemplos

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(−2)⁴ = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(-3)³ = (−3) ∙ (−3) ∙ (−3) = −27

Operações com símbolos de agrupamento

Eles geralmente parecem operações separadas com símbolos de agrupamento: parênteses, suportes e chaves. Estes são eliminados de dentro para fora, levando em consideração o seguinte:

• Se um símbolo de agrupamento for precedido por um sinal positivo, ele poderá ser removido sem alterar os sinais do conteúdo, por exemplo: + (−3 + 5 - 1) = −3 + 5 - 1 = 1.
• Se um sinal negativo precede o símbolo do grupo, ele será retirado investindo o sinal do conteúdo, por exemplo: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
• Quando existem operações combinadas de soma, subtração, multiplicação e divisão, as propriedades associativas e distributivas podem ser usadas para conveniência.

Exercícios resolvidos

a) 10 + 10

Solução: 20

b) (-8) + (-3)

Solução: -11

c) (3) + (-10) 

Solução: -7

d) (5) x (-3)

Solução: -15

e) (-10) x (-10)

Solução: 100

f) (18) ÷ (-3)

Solução: -6

G) (-10) ÷ (-2)

Solução: 5

h) 4 - ( - 7 + 9)

Solução: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11− 9 = 2