Lei de Fórmula Faraday, Unidades, Experiências, Exercício,

O Lei de Faraday No eletromagnetismo, estabelece que um fluxo de campo magnético em mudança é capaz de induzir uma corrente elétrica em um circuito fechado.

Em 1831, o físico inglês Michael Faraday experimentou motoristas em movimento dentro de um campo magnético e também campos magnéticos variados que cruzavam motoristas fixos.

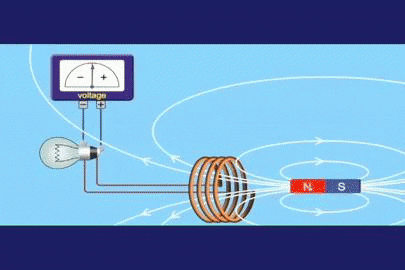figura 1. Experiência de indução de Faraday

Faraday percebeu que, se ele variar o fluxo de campo magnético no tempo, ele foi capaz de estabelecer uma tensão proporcional à referida variação. Se ε for a tensão ou força eletromotora induzida (feminino induzido) e φ é o fluxo do campo magnético, na forma matemática, ela pode ser expressa:

| ε | = Δφ/Δt

Onde o símbolo δ indica variação da quantidade e as barras no FEM indicam o valor absoluto deste. Como é um circuito fechado, a corrente pode circular em uma direção ou outra.

O fluxo magnético, produzido por um campo magnético através de uma superfície, pode variar de várias maneiras, por exemplo:

-Movendo um ímã de barra através de uma espiral circular.

-Aumentar ou diminuir a intensidade do campo magnético que atravessa o loop.

-Deixando o campo fixo, mas por algum mecanismo muda a área do loop.

-Combinando os métodos acima.

Figura 2. O físico inglês Michael Faraday (1791-1867).

[TOC]

Fórmulas e unidades

Suponha que haja um circuito fechado da área A, como uma espiral circular ou um insuor igual à Figura 1, e que existe um ímã que produz um campo magnético B.

O fluxo do campo magnético φ é uma quantidade escalar que se refere à quantidade de linhas de campo que atravessam a área a. Na Figura 1 estão as linhas brancas que deixam o pólo norte do ímã e retornam no sul.

Pode atendê -lo: Brayton Cycle: Process, Eficiência, Aplicações, Exercícios

A intensidade do campo será proporcional ao número de linhas por unidade de área, para que possamos ver que nos pólos é muito intenso. Mas podemos ter um campo muito intenso que não produz fluxo no loop, o que podemos alcançar alterando a orientação deste (ou do ímã).

Para levar em consideração o fator de orientação, o fluxo de campo magnético é definido como o produto escalar entre B e n, ser n O vetor unitário normal para a superfície da SPASE e que indica sua orientação:

Φ = B•n A = ba.cosθ

Onde θ é o ângulo entre B e n. Se, por exemplo, B e n Eles são perpendiculares, o fluxo do campo magnético é nulo, porque nesse caso o campo é tangente ao plano da SPASE e não pode atravessar sua superfície.

Em vez de B e n Eles são paralelos, isso significa que o campo é perpendicular ao plano spira e as linhas estão passando por ele ao máximo.

A unidade de sistema internacional para F é o Weber (W), onde 1 W = 1 T.m² (diz "Tesla por metro quadrado").

Lei de Lenz 

Na Figura 1, podemos ver que a polaridade da tensão muda à medida que o ímã se move. A polaridade é estabelecida pela lei de Lenz, que afirma que a tensão induzida deve se opor à variação que a produz.

Se, por exemplo, o fluxo magnético produzido pelo ímã aumentar, o motorista estabelece uma corrente que circula criando seu próprio fluxo, que se opõe a esse aumento.

Se, pelo contrário, o fluxo criado pelo ímã diminuir, a corrente induzida circula de tal maneira que seu próprio fluxo neutralize disse uma diminuição.

Pode atendê -lo: escalas termométricas

Para levar em consideração esse fenômeno, um sinal negativo para a lei de Faraday é colocado antes e não é mais necessário colocar as barras de valor absoluto:

ε = -Δφ/Δt

Esta é a lei de Faraday-Lenz. Se a variação do fluxo for infinitesimal, os deltas serão substituídos por diferenciais:

ε = -dφ/dt

A equação anterior é válida para um loop. Mas se tivermos uma bobina giratória, o resultado é muito melhor, porque o FEM multiplica N vezes:

ε = - n (dφ/dt)

Experimentos de Faraday

Para produzir a corrente que ilumina a lâmpada, entre o ímã e a espiral, deve haver um movimento relativo. Esta é uma das maneiras pelas quais o fluxo pode variar, porque dessa maneira a intensidade do campo que atravessa o loop muda.

No momento, o movimento do ímã cessa, a lâmpada sai, mesmo que o ímã ainda seja deixado na SPASE. O que é necessário para circular a corrente para a lâmpada é que o fluxo de campo varia.

Quando o campo magnético varia com o tempo, podemos expressá -lo como:

B = B (T).

Mantendo a área da SPASE constante e deixando -a fixada em um ângulo constante, que no caso da figura é 0º, então:

 Para o loop da Figura 1 (cos 0º = 1):

Spae de área variável

Se você puder alterar a área da SPASE, deixando sua orientação fixando e colocando -a no meio de um campo constante, o FEM induzido é dado por:

Uma maneira de conseguir isso é colocar uma barra que deslize em um trilho condutor a uma certa velocidade, como mostrado na figura a seguir.

Pode servir você: ÍO (satélite) Figura 3. Gerador deslizante. Fonte: Serway, r. Física para Ciência e Engenharia.

A barra e o trilho, mais uma lâmpada ou uma resistência conectada ao fio do motorista, formam um circuito fechado na forma de span.

Ao deslizar a barra, o comprimento x aumenta ou diminui e, com ela.

Variação do fluxo magnético por rotação

Como dissemos antes, se o ângulo entre B E o normal do loop é variado, o fluxo de campo muda de acordo com:

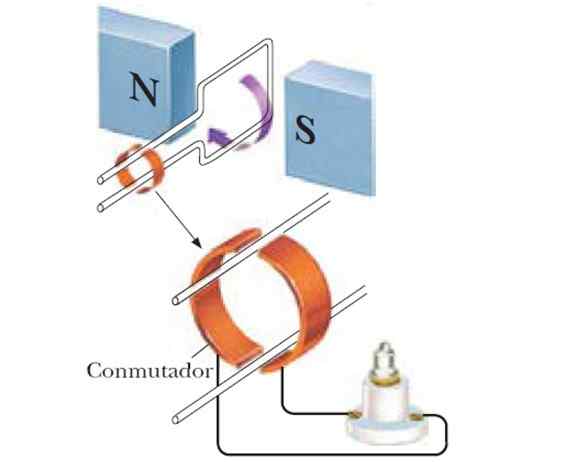Figura 4. Se o loop for girado entre os pólos de um ímã, um gerador sinusoidal será obtido. Fonte: f. Zapata.

Um gerador sinusoidal é obtido e, se um único número de bobinas forem usadas, o FEM induzido será maior:

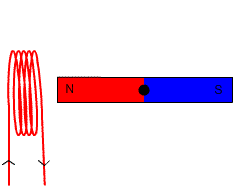Figura 5. Neste gerador, o ímã é girado para induzir a corrente na bobina. Fonte: Wikimedia Commons.

Exercício resolvido

Uma bobina circular de n voltas e rádio r, gira angularmente ω no meio de um campo magnético de magnitude B. Encontre uma expressão para o FEM máximo induzido na bobina.

Solução

A expressão para o FEM induzida pela rotação é aplicada quando a bobina tem n voltas, sabendo que:

-A área da bobina é A = πr²

-O ângulo θ varia dependendo do tempo como θ = ωt

É importante levar em consideração que θ = ωt é substituído pela primeira vez na lei de Faraday e então É derivado do tempo:

ε = -nba (cos θ) '= -nb (πr²).[cos (ωt)] '= nbω (πr²) Sen (ωt)

Como o FEM máximo é solicitado, isso ocorre sempre que sen ωt = 1, então finalmente:

ε_máx = Nbω (πr²)

Referências

1. Figueroa, d. 2005. Série: Física para Ciência e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB).
2. Giambattista, a. 2010. Física. Segunda edição. McGraw Hill.
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed. Prentice Hall.
4. Resnick, r. 1999. Físico. Vol. 2. 3ª ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V.
5. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 2.