Darcy Law

Explicamos qual é a lei de Darcy, suas equações, aplicações, limitações e propomos um exercício a ser resolvido

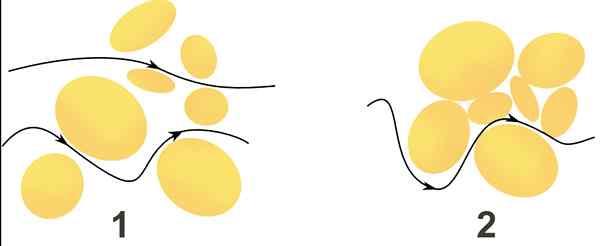
O fluxo de água através de dois meios porosos é indicado através de setas pretas. No meio 1, o fluxo se move mais rápido do que no meio do dia, uma vez que a velocidade depende do tamanho dos interstícios e da facilidade de comunicação entre eles. Fonte: Wikimedia Commons.

Qual é a lei de Darcy?

O Darcy Law É uma relação matemática aplicável ao fluxo de fluidos em meio permeável ou poroso, por exemplo, a água que drena na areia.

À medida que o fluido avança através do poroso, sua pressão hidrostática é variando, especificamente é maior nos pontos mais próximos da fonte e mais baixa nos pontos mais próximos da drenagem. Dessa maneira.

Por outro lado, o meio poroso é caracterizado por uma quantidade chamada Condutividade hidráulica K. Há claramente uma relação entre a porosidade, determinada por k, o gradiente hidráulico I e o fluxo por unidade de seção transversal q q.

A relação entre eles foi descoberta pelo engenheiro hidráulico francês Henry Darcy (1803-1858), que estava encarregado do abastecimento de água de sua cidade natal: Dijon.

A lei de Darcy foi apresentada em 1856, em um trabalho completo em que as quantidades físicas envolvidas na lei são detalhadas, os experimentos realizados e muito particularmente um aparelho chamado Permemeter.

Darcy Law Equations

A lei de Darcy mostra a relação entre várias quantidades físicas que descrevem o fluxo através de um meio poroso. Indica que o fluxo de água Q que se move por um certo meio poroso é diretamente proporcional à seção transversal perfurada e o gradiente hidráulico Yo:

Q ∝ a ∙ i

Pode servir a você: movimento retilíneo uniforme: características, fórmulas, exercícios

A constante de proporcionalidade é a permeabilidade k do ambiente poroso, também chamado Condutividade hidráulica. Dessa maneira, a lei de Darcy é apresentada como:

Q = k ∙ a ∙ i

Forma diferencial da lei de Darcy

A equação de Darcy pode ser expressa como uma relação diferencial entre a taxa de fluxo em cada ponto e o gradiente hidráulico local:

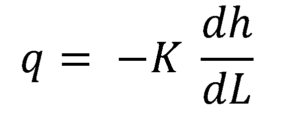
Como o gradiente hidráulico é uma quantidade negativa quando calculada na direção do fluxo, é necessário multiplicar pelo negativo da condutividade hidráulica para obter a taxa de fluxo médio q, em cada seção transversal.

Então as magnitudes presentes na lei de Darcy são analisadas em mais detalhes.

Fluxo, gradiente hidráulico e permeabilidade

1.- Fluxo q

O fluxo é definido como o volume de água que circula através de uma certa área de seção transversal até a direção do fluxo, por unidade de tempo:

Q = ΔV / ΔT

No sistema internacional de unidades de SI, o fluxo é medido em metros cúbicos por segundo, mas é frequentemente expresso em litros por minuto ou litros por segundo.

O fluxo por unidade de área q é frequentemente necessária, que é a razão entre o fluxo Q e a seção transversal:

Q = Q / A

No Si, q é expresso em m/s, e é por isso que q representa a velocidade média do fluido na seção transversal do tubo.

É importante observar que, enquanto o fluxo q é o mesmo em todas as seções do tubo, o fluxo por unidade de área q ou simplesmente a taxa de fluxo é maior nas seções mais estreitas e menores da maior parte.

2.- Gradiente hidráulico i

Quando um fluido circula ao longo de um meio poroso, a pressão hidrostática diminui na mesma direção do fluxo.

Pode servir a você: TON: Transformações, equivalências e exercícios resolvidos

Sabe -se que a pressão hidrostática, em um determinado ponto do tubo, é proporcional à altura h que marca um medidor de pressão do tubo aberto naquele local. A constante de proporcionalidade é o produto da densidade do fluido devido à aceleração da gravidade.

Dessa maneira, o gradiente hidráulico I é definido como a razão entre a diferença de altura ΔH das colunas de dois manômetros e ΔL, sendo esta a distância que separa os manóteres (veja a figura abaixo):

I = ΔH / ΔL

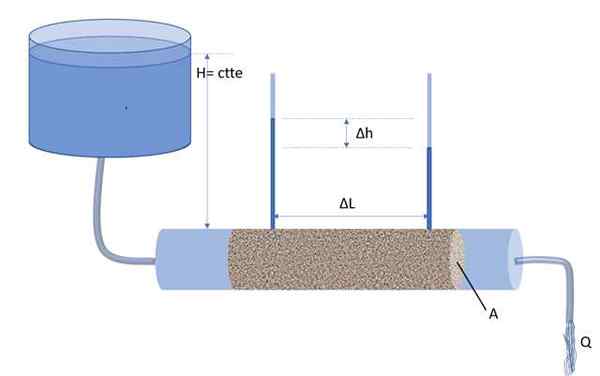O Permemetro, um aparelho inventado por Henry Darcy para quantificar o fluxo de água através de um meio poroso. Fonte: f. Zapata.

Este é o gradiente hidráulico médio na seção de ΔL longo, uma quantidade adimensional e também negativa.

Se você deseja encontrar o gradiente hidráulico em cada ponto do tubo, o limite é levado para ΔL tendendo a zero, resultando na derivada da função de gradiente hidráulico em relação à posição L, ao longo do fluxo:

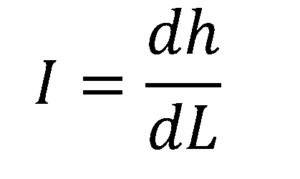
3.- Permeabilidade k

A permeabilidade de um meio poroso ou a condutividade hidráulica é a proporção entre o fluxo Q e o produto da seção transversal PARA Para o gradiente hidráulico Yo:

K = q / a ∙ i

A condutividade hidráulica tem unidades de velocidade, metros acima de si.

Uma unidade para K foi definida, chamada Darcy, Em homenagem a Henry Darcy e definido da seguinte forma:

A Darcy É a permeabilidade de um mililitro fluido, com uma viscosidade de uma centopéia, que se move ao longo de um centímetro em uma pressão diferencial de uma atmosfera, através de uma seção transversal de um centímetro quadrado.

Darcy Law Applications

A principal aplicação da lei de Darcy é prever o fluxo de água ao longo de um aqüífero, antes de perfurar poços.

Pode atendê -lo: análise dimensional

Além disso, a lei de Darcy é usada regularmente em engenharia agrícola e hidrológica. Também pode ser usado na indústria de petróleo para descrever o fluxo de gás e óleo em meios porosos. No entanto, nesse caso, K pode variar, dependendo do fluxo de gás ou óleo e pode não depender apenas e exclusivamente do substrato permeável.

Limitações

A lei de Darcy assume que a condutividade hidráulica k é uma quantidade do meio, o que é verdadeiro em muitos casos. No entanto, às vezes K depende da viscosidade dinâmica do fluido, que por sua vez pode depender da taxa de fluxo e dos gradientes de temperatura.

A suposição de Darcy é plausível ao considerar a água subterrânea, onde a viscosidade é praticamente constante, uma vez que seu valor quase não é afetado em vista das poucas diferenças de temperatura em todo o aqüífero.

Nos casos de fluxo de óleo por meios porosos, a equação de Darcy não pode ser aplicada conforme apresentado aqui, mas certas modificações são incorporadas que vão além do objetivo deste artigo.

Exercício resolvido

Determine a condutividade hidráulica de uma areia na praia, usando um permemeter de laboratório.

Suponha que o tubo do Permemeter tenha um diâmetro de 20 cm e que a distância entre os dois manômetros seja de 50 cm. Sabe -se também que a água flui a uma taxa de 300 decímetros cúbicos por minuto e a diferença de nível entre os dois manômetros é de 25 cm.

Solução

O fluxo que é 300 decímetros cúbicos por minuto, mas expressando em unidades do sistema internacional seria assim:

Q = 300 x 10^-3 m³ / 60 s = 5 x 10^-3 m³ / s

A seção transversal A é calculada por:

A = π ∙ r² = π ∙ (10 cm)² = π ∙ (0,1 m)² = 0,314 m²

O gradiente hidráulico I é um quociente entre a diferença de altura manométrica e a separação dos manômetros:

I = 25 cm / 50 cm = 0,5

De acordo com a definição de condutividade hidráulica k dada acima:

K = q / a ∙ i = (5 x 10^-3 m³ / s) / (0,314 m² ∙ 0,5) = 3.185 x 10^-2 m/s ≈ 2 m/min.