Explicação da lei de Coulomb, fórmula e unidades, exercícios, experimentos

O Lei de Coulomb É a lei física que governa a interação entre objetos carregados eletricamente. Foi afirmado pelo cientista francês Charles Augustin de Coulomb (1736-1806), graças aos resultados de seus experimentos através do equilíbrio de torção.

Em 1785, Coulomb experimentou inúmeras vezes com pequenas esferas de carga eletricamente, por exemplo, trazendo ou duas esferas, variando a magnitude de sua carga e também seu sinal. Sempre assistindo e registrando cuidadosamente cada resposta.

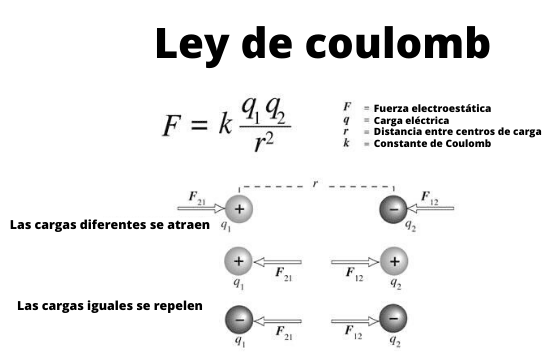
figura 1. Esquema que mostra a interação entre cargas elétricas específicas através da lei de Coulomb.

Essas pequenas esferas podem ser consideradas como Cargas específicas, isto é, objetos cujas dimensões são insignificantes. E eles cumprem, como se sabe desde a época dos gregos antigos, que as cargas do mesmo sinal são repelidas e as de diferentes sinais são atraídas.

Figura 2. O engenheiro militar Charles Coulomb (1736-1806) é considerado o físico mais importante da França. Fonte: Wikipedia Commons.

Com isso em mente, Charles Coulomb encontrou o seguinte:

-A força de atração ou repulsão entre duas cargas específicas é diretamente proporcional ao produto da magnitude das cargas.

-Essa força é sempre direcionada ao longo da linha que se junta às cargas.

-Finalmente, a magnitude da força é inversamente proporcional ao quadrado da distância que separa as cargas.

[TOC]

Fórmula e unidades da lei de Coulomb

Graças a essas observações, Coulomb concluiu que a magnitude da força F Entre duas cargas específicas q₁ e q₂, separou uma distância r, É matematicamente dado como:

Como a força é uma magnitude vetorial, para expressá -la, um vetor de unidade é completamente definido r Na direção da linha que une as cargas (um vetor de unidade tem magnitude igual a 1).

Além disso, a proporcionalidade necessária constante transformando a expressão anterior em uma igualdade é chamada k_e ou simplesmente k: o constante eletrostática qualquer Coulomb constante.

Finalmente, a lei de Coulomb para cargas pontuais é estabelecida, dada por:

A força, como sempre no sistema internacional de unidades, vem em Newton (n). Quanto às acusações, a unidade é chamada Coulomb (C) em homenagem a Charles Coulomb e, finalmente, a distância R vem em metros (M).

Observando atentamente a equação anterior, fica claro que a constante eletrostática deve ter unidades de n.m² / C², Para obter Newtons como resultado. O valor da constante foi determinado experimentalmente como:

Pode atendê -lo: vetores gratuitos: propriedades, exemplos, exercícios

k_e = 8.89 x 10 ⁹ N.m² / C² ≈ 9 x 10 ⁹ N.m² / C²

A Figura 1 ilustra a interação entre duas cargas elétricas: quando são o mesmo sinal, são repelidas, caso contrário, atraem.

Observe que a lei de Coulomb se encaixa na terceira lei ou lei de ação e reação de Newton, portanto as magnitudes de F₁ e F₂ Eles são iguais, o endereço é o mesmo, mas os sentidos são opostos.

Como aplicar a lei de Coulomb

Para resolver as interações entre as taxas elétricas, o seguinte deve ser levado em consideração:

- A equação é aplicada exclusivamente no caso de cargas específicas, ou seja, objetos carregados eletricamente, mas de dimensões muito pequenas. Se objetos carregados tiverem dimensões mensuráveis, é necessário dividi -las em cargas muito pequenas e depois adicionar as contribuições de cada uma dessas cargas, para as quais o cálculo abrangente é necessário.

- Força elétrica é uma magnitude vetorial. Se houver mais de duas cargas interagindo, a força líquida na carga q_Yo É dado pelo princípio da superposição:

F_Líquido = F_i1 + F_I2 + F_i3 + F_i4 +… = ∑ F_{eu j}

Onde o subscrito J Vale 1, 2, 3, 4 ... e representa cada uma das cargas restantes.

- Deve sempre ser consistente com as unidades. O mais frequente é trabalhar com a constante eletrostática nas unidades, se você precisar garantir que as cargas estejam em Coulomb e as distâncias nos medidores.

- Finalmente, a equação é aplicada quando as cargas estão em equilíbrio estático.

Exercícios resolvidos

- Exercício 1

Na figura seguinte, existem duas cargas específicas +q e +2q. Uma terceira carga pontual -Q é colocada em P. É solicitado a encontrar a força elétrica nessa carga devido à presença dos outros.

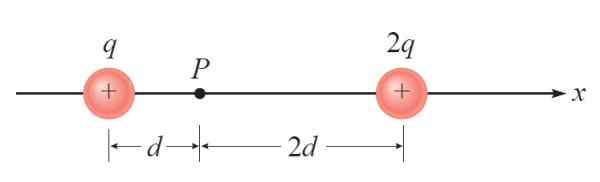Figura 3. Diagrama para o ano resolvido 1. Fonte: Giambattista, A. Física.

Solução

A primeira coisa é estabelecer um sistema de referência apropriado, que neste caso é o eixo horizontal ou o eixo x. A origem deste sistema pode estar em qualquer lugar, mas, por conforto, será colocado em P, como mostra a Figura 4A:

Pode servir você: Bethelgeuse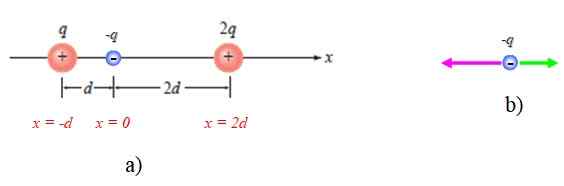Figura 4. Esquema para o ano resolvido 1. Fonte: Giambattista, A. Física.

Também é mostrado um esquema das forças -q, levando em consideração que é atraído para os outros dois (Figura 4b).

Vamos ligar F₁ Para a força que exerce a carga que, na carga -q, eles são direcionados ao longo do eixo x e pontos no sentido negativo, portanto:

O vetor unitário na direção do eixo x é x Com um sotaque circunflexo na equação. Esta é uma notação comum para um vetor de unidade. O menor sinal aparece porque a força F₁ pontos no sentido negativo do eixo.

Análogo é calculado F₂:

Observe que a magnitude de F₂ É metade do F₁, Embora a carga seja dupla. Para encontrar a força líquida, eles são finalmente adicionados F₁ e F₂:

F_Líquido = (-k + k/2).(Q² /d²) (x) N = - (K/2).(Q² /d²) (x) N

- Exercício 2

Dois esferitas de poliestireno de massa igual m = 9.0 x 10^-8 kg têm a mesma carga positiva q e são suspensos por um fio de seda em comprimento l = 0,98 m. As esferas são separadas a uma distância de d = 2 cm. Calcular o valor de.

Solução

A situação da declaração é descrita na Figura 5a.

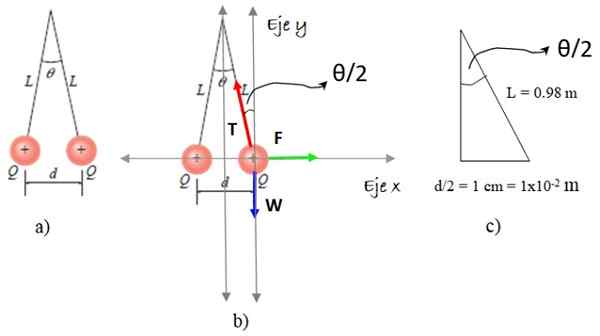Figura 5. Esquemas para a resolução do Exercício 2. Fonte: Giambattista, A. Física /F. Zapata.

Escolhemos um dos esferitas e, nela, desenhamos o diagrama corporal isolado, que inclui três forças: peso C, Tensão de corda T e repulsão eletrostática F, Como aparece na Figura 5b. E agora os passos:

Passo 1

O valor de θ/2 é calculado com o triângulo da Figura 5c:

θ/2 = Arcsen (1 x 10^-2/0.98) = 0.585º

Passo 2

Então você deve aplicar a segunda lei de Newton e a correspondência 0, já que as acusações estão em saldo estático. É importante destacar essa tensão T Está inclinado e tem dois componentes:

∑f_x = -T.sin θ + f = 0

∑f_e = T.cos θ - w = 0

etapa 3

Limpamos a magnitude da tensão da última equação:

Pode servir a você: Dinâmica: História, que estudos, leis e teorias

T = w/ cos θ = mg/ cos θ

Passo 4

Este valor é substituído na primeira equação para encontrar a magnitude de f:

F = t sin θ = mg (sin θ / cos θ) = mg. Tg θ

Etapa 5

Como f = k q² /d², Limpa Q:

Ao substituir os valores numéricos fornecidos pela declaração, é obtido:

Q = 2 × 10^-onze C.

Experimentos

Verificar a lei de Coulomb é simples por meio de um equilíbrio de torção semelhante ao usado em seu laboratório.

Existem duas pequenas esferas de saúco, uma das quais, a que no centro da balança é suspensa de um fio. O experimento consiste em tocar nas esferas saúco baixadas com outra esfera de metal carregada com carga q.

Figura 6. Equilíbrio de torção de Coulomb.

Imediatamente a carga é distribuída igualmente entre as duas esferas Saúco, mas então, assim como o mesmo sinal, eles repelir. Uma força que causa a torção do fio do fio e imediatamente se afasta da esfera fixa age na esfera suspensa.

Então vemos que ele varia algumas vezes até que o equilíbrio chegue. Em seguida, a torção da barra ou fio que a mantém é equilibrada pela força de repulsão eletrostática.

Se as esferas estivessem originalmente em 0, agora a esfera móvel terá transformado um ângulo θ. Ao redor do equilíbrio, há uma fita de graduação em graus para medir este ângulo. Ao determinar anteriormente a constante de torção, a força de repulsa e o valor da carga adquirida pelas esferas Saúco é facilmente calculada.

Referências

1. Figueroa, d. 2005. Série: Física para Ciência e Engenharia. Volume 5. Eletrostática. Editado por Douglas Figueroa (USB).
2. Giambattista, a. 2010. Física. Segunda edição. McGraw Hill.
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Resnick, r. 1999. Físico. Vol. 2. 3ª ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V.
5. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 2.