Gravicentro

Qual é o imposto?

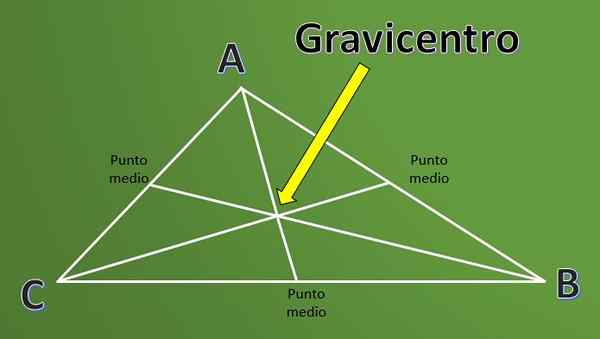
Ele Gravicentro É uma definição que é amplamente utilizada na geometria ao trabalhar com triângulos. Para entender a definição de gravicentro, é necessário conhecer a definição de "meio" de um triângulo.

As medianas de um triângulo são os segmentos de linha que começam em cada vértice e atingem o ponto médio do lado oposto ao referido vértice.

O ponto de interseção dos três medianos de um triângulo é chamado baricentro ou também é conhecido como tributação. Não basta apenas saber a definição, é interessante saber como esse ponto é calculado.

Cálculo do baricenteiro

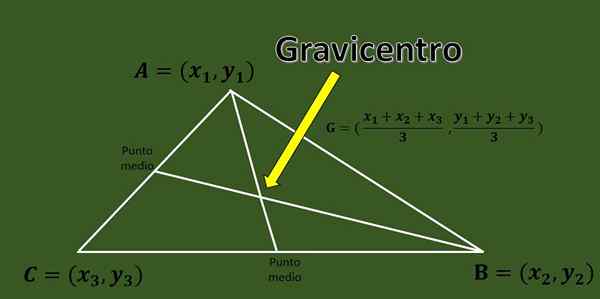
Dado um triângulo ABC com vértices a = (x1, y1), b = (x2, y2) e c = (x3, y3), o graviquentro é a interseção dos três medianos do triângulo.

Uma fórmula rápida que permite o cálculo da tributação de um triângulo, as coordenadas de seus vértices conhecidos é:

G = ((x1+x2+x3)/3, (y1+y2+y3)/3).

Com esta fórmula, você pode conhecer a localização do gravicento no avião cartesiano.

Características do imposto

Não é necessário rastrear os três medianos do triângulo, porque ao desenhar dois deles será evidenciado onde a tributação é.

A taxa de impostos divide cada mediana em 2 partes cuja proporção é 2: 1, ou seja, os dois segmentos de cada mediana são divididos em segmentos de comprimentos 2/3 e 1/3 do comprimento total, sendo maior a distância daquele que existe O que há entre o vértice e o folheto.

A imagem a seguir ilustra melhor esta propriedade.

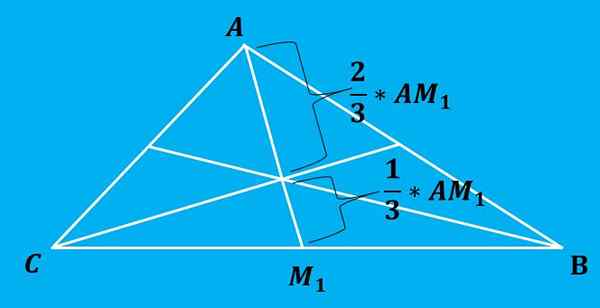
A fórmula para o cálculo da tributação é muito simples de aplicar. A maneira de obter essa fórmula é calculando as equações retas que cada mediana define e depois encontrar o ponto de corte dessas linhas.

Exercícios

Abaixo está uma pequena lista de problemas no cálculo do baricenter.

1.- Dado um triângulo de vértices a = (0,0), b = (1,0) e c = (1,1), calcule a tributação do referido triângulo.

Usando a fórmula dada, pode -se concluir rapidamente que o gravicento do triângulo ABC é:

G = ((0+1+1)/3, (0+0+1)/3) = (2/3, 1/3).

2.- Se um triângulo possui vértices a = (0,0), b = (1,0) e c = (1/2.1), quais são as coordenadas da tributação?

Como os vértices do triângulo são conhecidos, a fórmula para o cálculo da tributação é aplicada. Portanto, o Gravicentro tem coordenadas:

G = ((0+1+1/2)/3, (0+0+1)/3) = (1/2, 1/3).

3.- Calcule os possíveis contribuintes para um triângulo equilátero, de modo que dois de seus vértices sejam A = (0,0) e B = (2,0).

Neste exercício, apenas dois vértices do triângulo estão sendo especificados. Para encontrar os possíveis gravicentos, o terceiro vértice do triângulo deve primeiro calcular.

Como o triângulo é equilateral e a distância entre A e B é 2, o terceiro vértice C deve estar a uma distância 2 de A e B.

Usando o fato de que em um triângulo equilátero a altura coincide com a mediana e também usando o teorema de Pitágoras, pode -se concluir que as opções para as coordenadas do terceiro vértice são C1 = (1, √3) ou C2 = (1, 1, - - - √3).

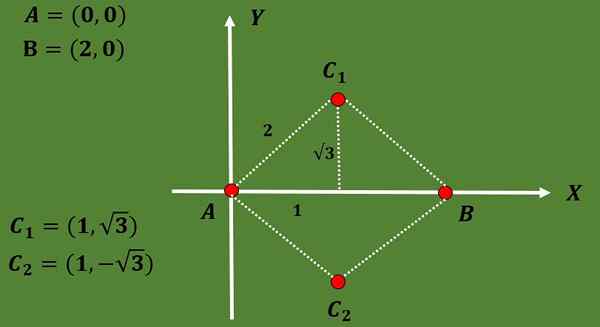
Para que as coordenadas dos dois possíveis graviques sejam:

G1 = ((0+2+1)/3, (0+0+√3)/3) = (3/3, √3/3) = (1, √3/3),

G2 = ((0+2+1)/3, (0+0 -√3)/3) = (3/3, -√3/3) = (1, -√3/3).

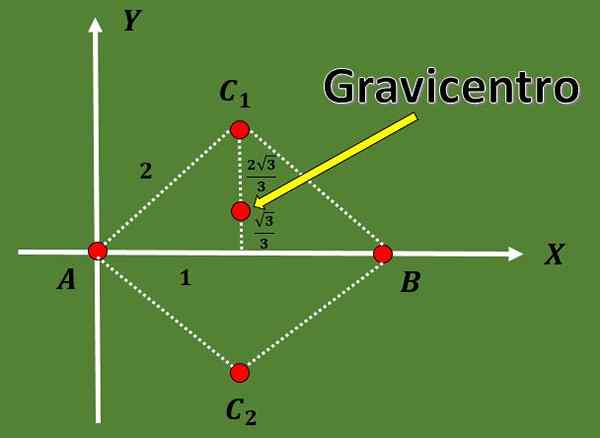
Graças às contas anteriores, também pode -se notar que a mediana é dividida em duas partes cuja proporção é 2: 1.