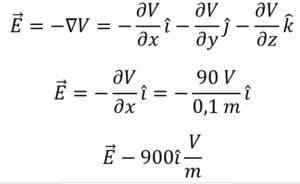Gradiente potencial

Qual é o gradiente potencial?

Ele Gradiente potencial É um vetor que representa a taxa de mudança do potencial elétrico em relação à distância em cada eixo de um sistema de coordenadas cartesianas. Assim, o vetor de gradiente potencial indica o endereço em que a taxa de câmbio do potencial elétrico é maior, dependendo da distância.

Por sua vez, o módulo de gradiente potencial reflete a taxa de mudança na variação potencial elétrica em uma direção específica. Se houver conhecimento do valor disso em cada ponto de uma região espacial, o campo elétrico poderá ser obtido do potencial gradiente.

O campo elétrico é definido como um vetor, que tem uma direção e magnitude específicas. Ao determinar a direção em que o potencial elétrico diminui mais rapidamente - será o ponto de referência - e, ao dividir esse valor pela distância percorrida, a magnitude do campo elétrico é obtida.

Características do potencial gradiente

O gradiente em potencial é um vetor delimitado por coordenadas espaciais específicas, que mede a taxa de mudança entre o potencial elétrico e a distância percorrida pelo referido potencial. 

As características mais destacadas do gradiente de potencial elétrico estão detalhadas abaixo:

1- O gradiente em potencial é um vetor. Portanto, tem uma magnitude e direção específicas.

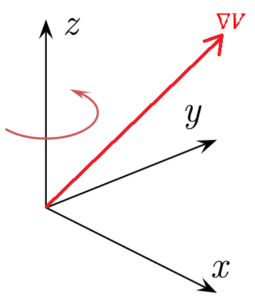
2- Como o gradiente potencial é um vetor no espaço, ele tem magnitudes direcionadas nos eixos X (largura), Y (alta) e Z (profundidade), se o sistema de coordenadas cartesiano for tomado como uma referência.

Pode atendê -lo: faltando sistema operacional: o que isso significa e como resolvê -lo

3- Este vetor é perpendicular à superfície do equipamento no ponto em que o potencial elétrico é avaliado.

4- O vetor de gradiente potencial é direcionado para a direção da variação máxima da função potencial elétrica em qualquer ponto.

5- O módulo de gradiente potencial é igual à derivada da função potencial elétrica em relação à distância percorrida na direção de cada um dos eixos do sistema de coordenadas cartesianas.

6- O gradiente em potencial tem valor zero nos pontos estacionários (máximo, mínimo e pontos de cadeira).

7- No sistema internacional de unidades (SI), as unidades de medição de gradiente em potencial são volts/medidores.

8- A direção do campo elétrico é a mesma em que o potencial elétrico diminui sua magnitude mais rapidamente. Por sua vez, o potencial gradiente pontos na direção em que o potencial aumenta seu valor em relação a uma mudança de posição. Então, o campo elétrico tem o mesmo valor do gradiente em potencial, mas com o sinal oposto.

Como calcular?

A diferença no potencial elétrico entre dois pontos (ponto 1 e 2) é dada pela seguinte expressão:

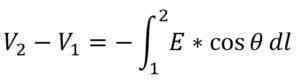
Onde:

• V1: potencial elétrico no ponto 1.
• V2: potencial elétrico no ponto 2.
• E: magnitude do campo elétrico.
• Ѳ: ângulo a inclinação do vetor de campo elétrico medido em relação ao sistema de coordenadas.

Ao expressar esta fórmula diferencialmente, o seguinte a seguir:

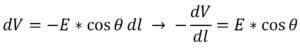
O fator E*cos (ѳ) refere -se ao módulo do componente de campo elétrico na direção do DL. Seja l o eixo horizontal do plano de referência, depois cos (ѳ) = 1, como este:

Pode atendê -lo: tecnologia

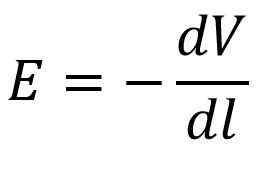
A seguir, o quociente entre a variação do potencial elétrico (DV) e a variação na distância percorrida (DS) é o potencial módulo de gradiente para o referido componente. 

A partir daí, segue -se que a magnitude do gradiente de potencial elétrico é igual ao componente do campo elétrico no endereço do estudo, mas com o sinal oposto.

No entanto, como o ambiente real é tridimensional, o gradiente em potencial em um determinado ponto deve ser expresso como a soma de três componentes espaciais nos eixos x e z e z do sistema cartesiano.

Quando o vetor de campo elétrico data em seus três componentes retangulares, você tem o seguinte:

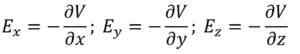
Se houver uma região no plano em que o potencial elétrico tenha o mesmo valor, o derivado parcial desse parâmetro em relação a cada uma das coordenadas cartesianas será anulada.

Assim, em pontos no equipamento, a intensidade do campo elétrico terá zero magnitude.

Finalmente, o potencial vetor de gradiente pode ser definido como exatamente o mesmo vetor de campo elétrico (em magnitude), com o sinal oposto. Assim, você tem o seguinte:

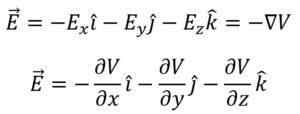
Exemplo

Dos cálculos anteriores que você precisa:

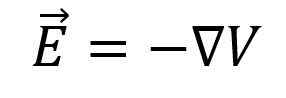
No entanto, antes de determinar o campo elétrico, dependendo do gradiente em potencial, ou vice -versa, a direção em que a diferença de potencial elétrico cresce deve ser determinada primeiro.

Depois disso, o quociente da variação do potencial elétrico e a variação da distância líquida percorrida é determinada.

Dessa maneira, é obtida a magnitude do campo elétrico associado, o que é igual à magnitude do gradiente potencial nessa coordenada.

Pode atendê -lo: 23 vantagens e desvantagens de estudar online

Exercício

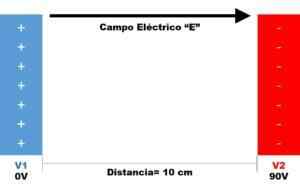
Existem duas placas paralelas, como refletido na figura a seguir.

Passo 1

O endereço de crescimento do campo elétrico no sistema de coordenadas cartesiano é determinado.

O campo elétrico cresce apenas na direção horizontal, dada o arranjo de placas paralelas. Consequentemente, é viável deduzir que os componentes do gradiente potencial no eixo y e o eixo z são nulos.

Passo 2

Os dados de juros são discriminados contra.

• Diferença de potencial: dv = v2 - v1 = 90 v - 0 v => dv = 90 v.
• Distância Diferença: DX = 10 centímetros.

Para garantir a congruência das unidades de medição usadas de acordo com o sistema internacional de unidades, as magnitudes que não são expressas em si devem ser convertidas conforme apropriado. Assim, 10 centímetros equivalem a 0,1 metros e, finalmente: dx = 0,1 m.

etapa 3

A magnitude do potencial vetor de gradiente é calculada conforme apropriado.