Tipos de funções transcendentes, definição, propriedades, exemplos

As Funções transcendentes Os elementos são funções trigonométricas exponenciais, logarítmicas, trigonométricas e inversas, hiperbólicas hiperbólicas e inversas. Ou seja, eles são aqueles que não podem ser expressos por uma proporção polinomial, polinomial ou raízes polinomiais. 

As funções transcendentes não elementares também são conhecidas como funções especiais e, entre elas, a função de erro pode ser nomeada. As funções algébricas (polinômios, quocientes polinomiais e raízes polinomiais) ao lado do Funções transcendentes Elementais constituem o que em matemática é conhecido como Funções elementares.

Também é considerado funções transcendentes que resultam de operações entre funções transcendentes ou entre funções transcendentes e algébricas. Essas operações são: a soma e a diferença de funções, produto e proporção de funções, bem como a composição de duas ou mais funções.

[TOC]

Definição e propriedades

Função exponencial

É uma função real da variável independente real da forma:

f (x) = a^x = a^x

onde para É um número real positivo (A> 0) corrigido chamado de base. Circunflejo ou supervisão são usados ​​para denotar a operação de potencialização.

Vamos colocar por precaução A = 2 Então a função é assim:

f (x) = 2^x = 2^x

Que será avaliado para vários valores da variável independente x:

Abaixo está um gráfico em que a função exponencial para vários valores básicos é representada, incluindo a base e (Número Neper e ≃ 2.72). A base e É tão importante que, em geral, ao falar sobre função exponencial, você pensa sobre E^x, Isso também é denotado exp (x).

figura 1. Função exponencial a^x, para vários valores da base a. (Elaboração própria)

Propriedades da função exponencial

Na Figura 1, pode -se observar que o domínio das funções exponenciais são números reais (dom f = R) e o alcance ou rota são os reais positivos (executados f = R⁺). 

Pode atendê -lo: simetria

Por outro lado, independentemente do valor da base A, todas as funções exponenciais passam pelo ponto (0, 1) e pelo ponto (1, a). 

Quando a base A> 1, Então a função está crescendo e quando 0 < a < 1 A função está diminuindo. 

As curvas de y = a^x e de y = (1/a)^x  Eles são simétricos em relação ao eixo E. 

Com exceção do caso A = 1, A função exponencial é injetiva, isto é, para cada valor da imagem, um corresponde e apenas um valor inicial.

Função logarítmica

É uma função real real da variável independente real com base na definição do logaritmo de um número. Logaritmo baseado para de um número x, É o número e para o qual a base deve ser levantada para obter o argumento x:

registro_para(x) = y ⇔ a^y = x

Isto é, o função logaritmo na base para É a função inversa à função exponencial com base em para.

Por exemplo:

registro₂1 = 0, desde 2^0 = 1

Outro caso, log₂4 = 2, porque 2^2 = 4

O logaritmo raiz de 2 é log₂√2 = ½, porque 2^½ = √2

registro₂ ¼ = -2, em vista que 2^(-2) = ¼ 

Abaixo está um gráfico da função logaritmo em várias bases.

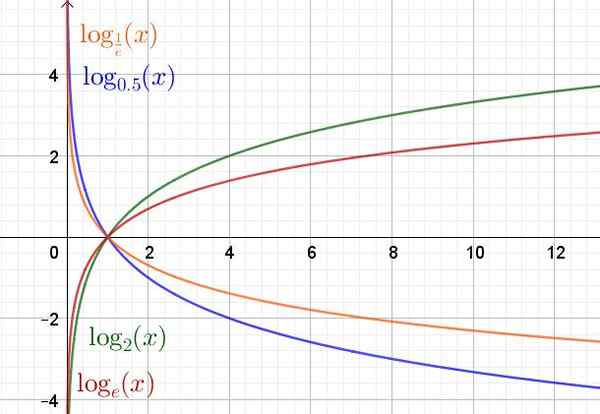Figura 2. Função exponencial para diferentes valores de base. (Elaboração própria)

Propriedades da função logaritmo

O domínio da função logaritmo e (x) = logpara(x)  Eles são os números reais positivos R+. O alcance ou rota são os números reais R.

Independentemente da base, a função logaritmo sempre passa pelo ponto (1.0) e o ponto (a, 1) pertence ao gráfico da referida função.

Pode servir a você: teoria da fila: história, modelo, para que serve e exemplos para

No caso de que a base a seja maior que a unidade (a> 1), a função logaritmo está aumentando. Mas sim (0 < a < 1) entonces es una función decreciente.

Seno, Coseno e funções tangentes

A função seno. Para obter o valor de sen (x) de um ângulo, o ângulo é representado no círculo unitário e a projeção do referido ângulo no eixo vertical é o peito correspondente a esse ângulo.

Abaixo está (na Figura 3) o círculo trigonométrico e a mama para vários valores angulares x1, x2, x3 e x4.

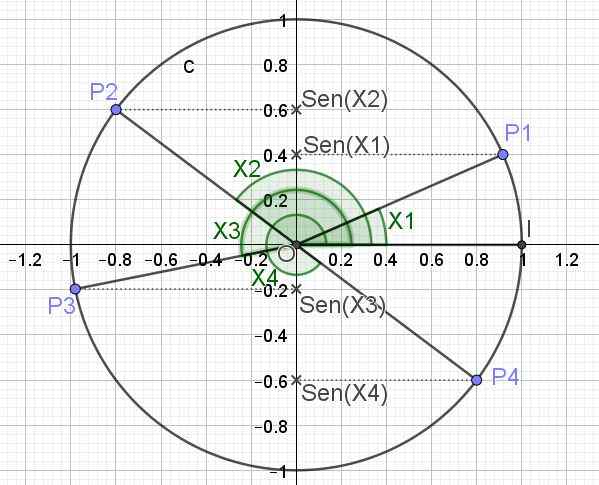Figura 3. Círculo trigonométrico e o seio de vários ângulos. (Elaboração própria)

Definido dessa maneira, o valor máximo que a função Sen (x) pode ter é 1, que ocorre quando x = π/2 + 2π n, sendo n um número inteiro (0, ± 1, ± 2). O valor mínimo que a função sen (x) pode levar quando x = 3π/2 + 2π n. 

A função Coseno y = cos (x) é definida de maneira semelhante, mas a projeção das posições angulares P1, P2, etc. é realizada no eixo horizontal do círculo trigonométrico.

Por outro lado, a função y = tan (x) é a razão entre a função seno.

Em seguida, é mostrado um gráfico das funções transcendentes sen (x), cos (x) e tan (x)

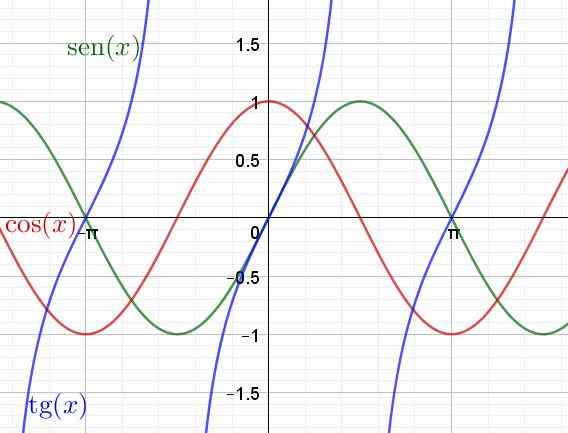Figura 4. Gráfico das funções transcendentes, mama, cosseno e tangente. (Elaboração própria)

Derivado e integral

Derivado da função exponencial

O derivado e' da função exponencial y = a^x É a função a^x multiplicado por ele Logaritmo neperiano da base a:

Pode servir a você: teoria do conjunto: características, elementos, exemplos, exercícios

e '= (a^x)' = a^x ln a

No caso particular da base e, A derivada da função exponencial é a própria função exponencial.

Integral da função exponencial

A integral indefinida de a^x É a função dividida entre o logaritmo neperiano da base. 

No caso particular da Base E, a integral da função exponencial é a própria função exponencial.

Tabela derivada e integral das funções transcendentes

Abaixo está uma tabela de resumo das principais funções transcendentes, seus derivados e indefinidos (antiderivativos):

Tabela derivada e integral indefinida para algumas funções transcendentes. (Elaboração própria)

Exemplos

Exemplo 1

Encontre a função resultante da composição da função f (x) = x^3 com a função g (x) = cos (x):

(f ou g) (x) = f (g (x)) = cos³(x)

Seu derivado e sua integral indefinida é:

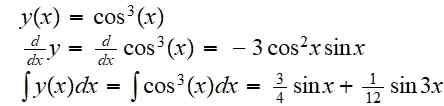
Exemplo 2

Encontre a composição da função G com a função f, sendo G e F as funções definidas no exemplo anterior:

(g ou f) (x) = g (f (x)) = cos (x³)

Deve -se notar que a composição das funções não é uma operação comutativa.

O derivado e o indefinido integral para esta função são respectivamente:

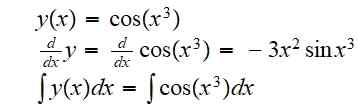
A integral foi deixada indicada porque não é possível escrever o resultado como uma combinação de funções elementares de uma maneira exata.

Referências

1. Cálculo de uma única variável. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 de novembro. 2008
2. O teorema da função implícita: história, teoria e aplicações. Steven G. Krantz, Harold R. Parques. Springer Science & Business Media, 9 de novembro. 2012
3. Análise multivariável. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 de dezembro. 2010
4. Dinâmica do sistema: modelagem, simulação e controle de sistemas mecatrônicos. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 de março. 2012
5. Cálculo: Matemática e Modelagem. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 de janeiro. 1999
6. Wikipedia. Função transcendente. Recuperado de: é.Wikipedia.com