Funções matemáticas

Uma função matemática é a relação entre duas magnitudes, quando a primeira depende do segundo. Shuttersock

O que são funções matemáticas?

As Funções matemáticas Eles são a expressão na linguagem matemática de uma relação entre duas variáveis, e o valor do primeiro das variáveis ​​depende do segundo. Normalmente, essas variáveis ​​são simbolizadas com as letras x e y.  A variável x é chamada de domínio ou variável independente; e para o y, codomínio ou variável dependente.

Vejamos um exemplo. Temos duas variáveis ​​ou magnitudes: dólar e centavos. Sabemos que 100 centavos são equivalentes a um dólar. Portanto, os centavos (x) é o domínio e o dólar (y) corresponde ao codomínio. Este relacionamento pode ser expresso com a seguinte função (f):

F (x) = y / 100

Se eu tiver 143 centavos no meu Piggy Bank e quero saber quantos dólares economizei, aplico apenas a função:

F (x) = 143 /100

Portanto, eu tenho $ 1,43.

Também podemos expressar o relacionamento inverso, ou seja, que um dólar é equivalente a 100 centavos. Consequentemente, as categorias das variáveis ​​são investidas: o dólar (x) se torna o domínio enquanto os centavos é o codomínio. Nós expressamos dessa maneira:

F (x) = x x 100

Se eu tenho US $ 1,43 no meu Piggy Bank, mas quero saber quantos centavos esse número é equivalente, é suficiente para aplicar esta segunda função.

F (x): 1,43 x 100

O resultado retorna aos meus 143 centavos originais.

As variáveis ​​das funções matemáticas

Uma variável é simplesmente um símbolo (x, y, z) que representa uma variedade de elementos.

No exemplo anterior, as variáveis ​​x e y simbolizavam o dólar e o centavo de dólar. Mas os mesmos símbolos (x e y) podem ser usados ​​para representar uma infinidade de elementos, como: idade de uma pessoa e seu peso; Número de voos para um determinado destino e um período de tempo (por semana, por mês, por ano), etc.

Pode atendê -lo: divisão sintética

As variáveis ​​podem ser classificadas em vários tipos, mas as mais relevantes para as funções matemáticas são as seguintes:

• Variável dependente: Aqueles cujo valor depende do valor atribuído a outras variáveis ​​dentro da função.
• Variável independente: Mudanças nesse tipo de variável influenciam os valores do restante das variáveis ​​da função.
• Variável quantitativa: É expresso por quantidades numéricas definidas. Eles podem ser números inteiros ou decimais.

Características das funções matemáticas

1- A relação entre as variáveis ​​é expressa em termos de equivalência.

2- Para cada valor de variável x existe a, e apenas um equivalente da variável e. E vice -versa: para um certo valor de y existe a, e apenas resultado da variável x.

3- Eles podem ser representados graficamente em um plano cartesiano, o que permite prever o comportamento de uma das variáveis ​​do outro.

4- A definição moderna de função matemática se deve ao matemático alemão Peter Dirichlet (1805-1859), que o publicou em 1837.

Tipos de funções matemáticas

As funções matemáticas podem ser classificadas de acordo com diferentes critérios, como o relacionamento estabelecido entre as variáveis ​​x e o comportamento matemático da função.

Entre os principais tipos estão os seguintes:

Funções algébricas

Eles são caracterizados por estabelecer uma relação entre componentes que são expressos por meio de um monomial ou polinomial. Esse relacionamento pode ser determinado através de operações matemáticas simples, como subtração, multiplicação, divisão, soma, potenciação ou transmissão.

Funções lineares

Quando representados em um avião cartesiano, eles aparecem com a forma de uma linha reta que corta o eixo de coordenadas em um determinado ponto. Daí o nome deles, embora eles também sejam conhecidos como funções de primeira grau.

Pode atendê -lo: fator comum: características, exemplos, exercícios

Funciona em pedaços

Neste tipo o valor do codomínio e altera o comportamento da função. Existem, portanto, dois intervalos com comportamento diferente em relação ao valor do domínio.

Funções transcendentes

São funções altamente complexas. Operações algébricas comuns não são suficientes (subtração, multiplicação, divisão, soma, potenciação ou radiação) para determinar a relação entre as variáveis, de modo que outras ferramentas matemáticas devem ser usadas, como derivados, integrais ou logaritmos.

Funções trigonométricas

Esse tipo de funções mostra a relação numérica que existe entre os vários elementos de um triângulo e outras figuras geométricas, especialmente entre seus ângulos. Fórmulas para a mama, cosseno, tangente, secante e harmonia são exemplos desse tipo de funções.

Funções injetivas

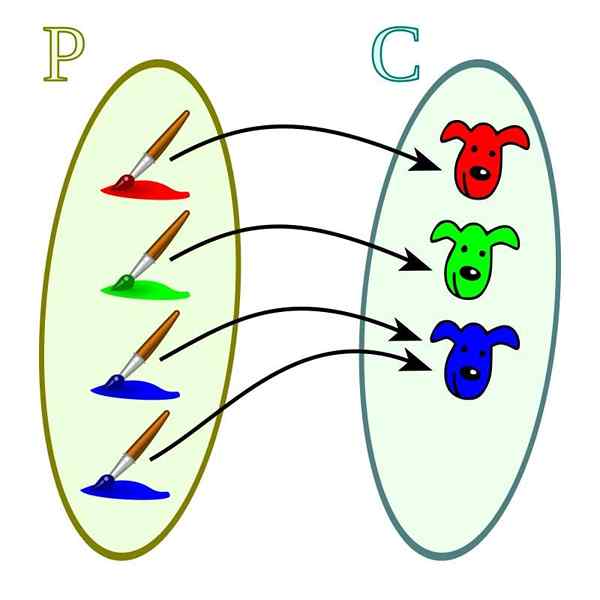
As funções desse tipo são caracterizadas pela particularidade da relação entre domínio e codomínio. Para cada um dos valores deste último, apenas um valor de domínio corresponde. Também pode acontecer que um valor de domínio não possua nenhum valor correspondente no codomínio.

Função injetiva. Fonte: Wikimedia Commons

Funções onjetivas

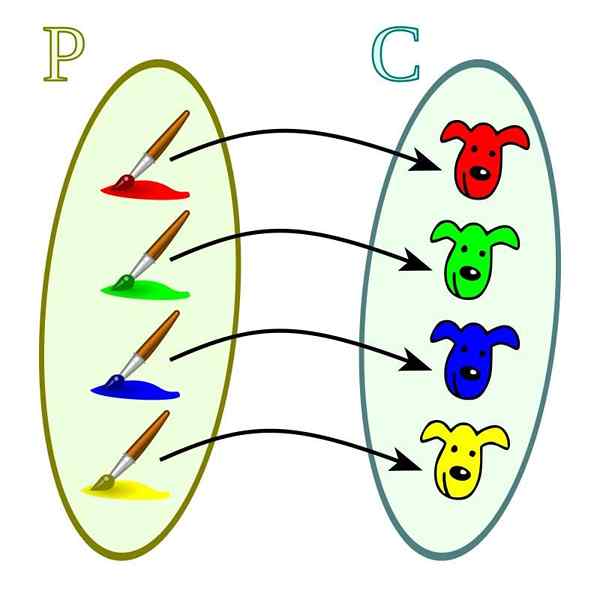
Nesse caso, cada uma das magnitudes do codomínio está relacionada a pelo menos um dos valores do domínio. Eles são distinguidos das funções injetivas nas quais os valores do codomínio podem estar relacionados a mais de um dos valores do domínio.

Função excessiva. Fonte: Wikimedia Commons

Funções bijectas

Este tipo de funções apresenta propriedades injetivas e superjetivas.

Quais são as funções matemáticas para?

As funções são amplamente utilizadas em todas as ciências que têm matemática como ciência auxiliar. Este é o caso de física, engenharia, medicina, finanças, estatísticas, entre muitos outros.

Pode servir a você: distribuição de frequência: como fazer uma tabela, exemplo, exercício

Na vida cotidiana

No entanto, também podemos ser úteis para resolver problemas mais simples do dia a dia.

Imagine que seu avô lhe deu 10 moedas, que você gastará em chocolate. No quiosque, você deu as 10 moedas ao dependente, dizendo para ele dar a você todos os chocolates que podem ser comprados com essa quantidade de moedas. Eles deram a você 5 chocolates. Qual é o preço de cada?

Propomos o problema: se 5 chocolates forem igual a 10 moedas, quantas moedas são equivalentes a um único chocolate?

Nossa variável independente (x) é a quantidade de chocolates (5), enquanto a variável dependente (y) corresponde ao número de moedas, ou seja, 10.

Nós expressamos a função da seguinte maneira:

F (x) = 2x/x

F (x) = 2 (5)/5

F (x) = 10/5

F (x) = 2

E já temos a resposta: cada chocolate custa 2 moedas.

Referências

1. (S/F). Funções elementares. O site de funções matemáticas. Retirado de unections.Volfrâmio.com.
2. (S/F). O que é uma função? Tirado de Mathsisfun.com.