Função homográfica como representar graficamente, exercícios resolvidos

O funçãoHomográfico ou racional Ón É um tipo de função matemática composta pela divisão de dois componentes polinomiais. Ele obedece à forma p (x)/q (x), onde q (x) não pode tomar a forma nula.

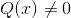
Por exemplo, a expressão (2x - 1)/(x + 3) corresponde a uma função homográfica com p (x) = 2x - 1 y q (x) = x + 3.

Fonte: Pixabay.com

As funções homográficas constituem uma seção de estudo das funções analíticas, sendo tratadas a partir da abordagem de gráfico e do domínio e estudo da faixa. Isso se deve às restrições e fundações que devem ser aplicadas para suas resoluções.

[TOC]

O que é uma função homográfica?

São expressões racionais de variável única, embora isso não signifique que não haja expressão semelhante para duas ou mais variáveis, onde já estaria na presença de corpos no espaço que obedecem aos mesmos padrões que a função homográfica no nível.

Eles têm raízes reais em alguns casos, mas a existência de assíntotas verticais e horizontais é sempre mantida, além de também o crescimento e diminuir os intervalos. Geralmente, apenas uma dessas tendências está presente, mas há expressões capazes de mostrar ambos em seu desenvolvimento.

Seu domínio é restrito pelas raízes do denominador, porque não há divisão entre zero de números reais.

Função homográfica mista

Eles são muito frequentes no cálculo, especialmente diferenciais e abrangentes, sendo necessários para derivar e anti -angel sob fórmulas específicas. Alguns dos mais comuns são classificados abaixo.

Nº par de função homográfica

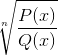
Exclui todos os elementos do domínio que tornam o argumento negativo. As raízes presentes em cada polinomial mostram valores zero quando avaliados.

Esses valores são aceitos pelo radical, embora a restrição fundamental da função homográfica deva ser considerada. Onde q (x) não pode receber valores nulos.

Pode atendê -lo: funções transcendentes: tipos, definição, propriedades, exemplos

As soluções de intervalos devem ser interceptadas:

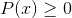
Para alcançar interseções, o método de sinal pode ser usado, entre outros.

Logaritmo de função homográfica

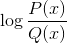
Exclui os valores de domínio que lançam intervalos negativos e zeros. Porque os zeros já estão excluídos do denominador, as soluções de: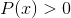

Também é comum encontrar ambas as expressões em uma, entre outras combinações possíveis.

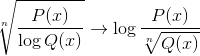
Como representar graficamente uma função homográfica?

Funções homográficas correspondem graficamente com hiperbolas no avião. Que são transportados horizontal e verticalmente de acordo com os valores que definem os polinômios.

Existem vários elementos que devemos definir para representar uma função racional ou homográfica.

Estado

O primeiro será as raízes ou zeros das funções p e q.

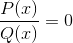
Os valores alcançados serão indicados no eixo x dos gráficos. Indicando as interseções do gráfico com o eixo.

Assíntota vertical

Corresponder às linhas verticais, que demarcaram o gráfico de acordo com as tendências que eles apresentam. Eles tocam o eixo x nos valores que fazem o denominador zero e nunca serão tocados pelo gráfico da função homográfica.

Assíntota horizontal

Representado por uma linha de ponto horizontal, demarcou um limite para o qual a função não será definida no ponto exato. As tendências serão observadas antes e depois desta linha.

Para calculá -lo, devemos recorrer a um método semelhante ao método L'Pomital, usado para resolver os limites de funções racionais que tendem ao infinito. Os coeficientes das mais altas poderes do numerador e o denominador da função devem ser tomadas.

Por exemplo, a seguinte expressão tem uma assíntota horizontal em y = 2/1 = 2.

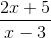
Intervalo de crescimento

Os valores do pedido terão tendências marcadas no gráfico devido às assíntotas. No caso de crescimento, a função aumentará dos valores à medida que os elementos do domínio da esquerda para a direita são avaliados.

Pode atendê -lo: 60 divisores

Intervalo decrescente

Os valores ordenados diminuirão à medida que os elementos do domínio da esquerda para a direita são avaliados.

Os saltos encontrados nos valores não serão levados em consideração à medida que aumenta ou diminui. Isso ocorre quando o gráfico está próximo de uma vertical ou Horizont.

Interseção com y

Fazendo zero o valor de x, é a interseção com o eixo das ordenadas. Este é um fato muito útil para obter o gráfico da função racional.

Exemplos

Defina o gráfico das seguintes expressões, encontre suas raízes, assíntotas verticais e horizontais, crescimento e diminuição de intervalos e interseção com o eixo do ordenado.

Exercício 1

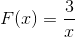
A expressão não tem raízes, porque tem um valor constante no numerador. A restrição a se aplicar será x diferente de zero. Com assíntota horizontal em y = 0 e assíntota vertical em x = 0. Não há pontos de interseção com o eixo e.

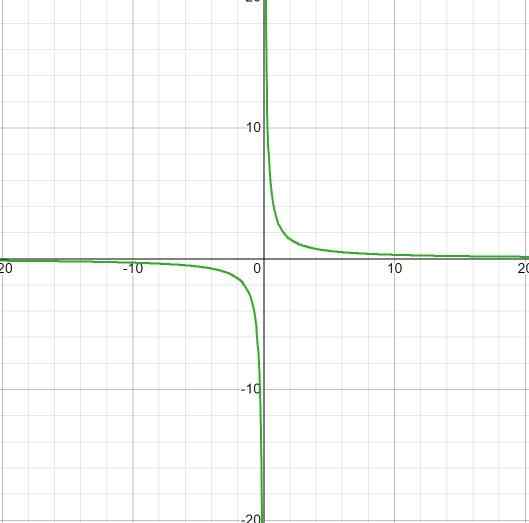
Observa -se que não há intervalos de crescimento, mesmo com o salto de menos para mais infinito em x = 0.

O intervalo de diminuição é

Id: (-∞; o) u (0, ∞)

Exercício 1.2

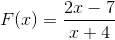
2 polinômios são observados como na definição inicial, por isso prosseguimos de acordo com as etapas estabelecidas.

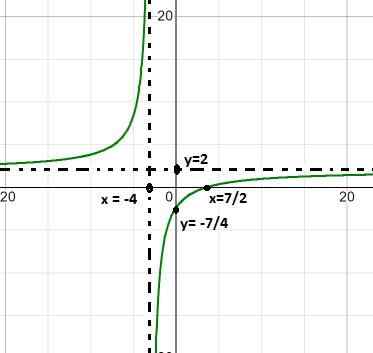
A raiz encontrada é x = 7/2 que resulta da equalização da função.

A assíntota vertical está em x = - 4, que é o valor excluído do domínio devido à condição de função racional.

A assíntota horizontal está em y = 2, depois de dividir 2/1, os coeficientes das variáveis ​​de grau 1.

Tem uma interseção com os ordenados em y = - 7/4. Valor encontrado após empatar o x a zero.

Pode servir a você: Fração equivalente a 3/5 (solução e explicação)

A função cresce constantemente, com um salto de mais para menos infinito ao redor da raiz x = -4.

Seu intervalo de crescimento é (-∞, - 4) u ( - 4, ∞).

Quando o valor de x é próximo a menos infinito, a função leva valores próximos a 2. O mesmo acontece quando o X se aproxima mais infinito.

A expressão se aproxima mais infinita quando avaliada em - 4 à esquerda e menos infinita quando avaliada em - 4 à direita.

Exercício 2

O gráfico da seguinte função homográfica é observada:

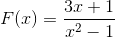
Descreva seu comportamento, raízes, assíntotas verticais e horizontais, intervalos de crescimento e diminuição e interseção com o eixo ordenado.

O denominador de expressão indica considerando a diferença de quadrados (x + 1) (x - 1) os valores das raízes. Dessa forma, ambas as assíntotas verticais podem ser definidas como:

x = -1 e x = 1

A assíntota horizontal corresponde ao eixo da abscissa porque o poder principal está no denominador.

Sua única raiz é definida por x = -1/3.

A expressão sempre diminui da esquerda para a direita. Ele se aproxima de zero quando tende ao infinito. Menos infinitamente ao se aproximar -1 à esquerda. Mais infinito ao se aproximar -1 à direita. Menos infinito ao se aproximar de 1 à esquerda e mais infinito ao se aproximar de 1 à direita.

Referências

1. Aproximação com funções racionais. Donald J. Novo homem. Soc matemático americano., 31 de dezembro. 1979
2. Funções de classificação ortogonais. Universidade de La Laguna Tenerife Adhemar Bulheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njstad. Cambridge University Press, 13 de fevereiro. 1999
3. Aproximação de classificação de funções reais. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 de março. 2011
4. Funções algébricas. Gilbert Ames Bliss. Couer Corporation, 1 de janeiro. 2004
5. Revista da Sociedade Matemática Espanhola, 5-6 Volumes. Sociedade Matemática Espanhola, Madri 1916