Propriedades da função exponencial, exemplos, exercícios

O função exponencial É uma função matemática de grande importância para os muitos aplicativos que tem. É definido da seguinte maneira:

f (x) = b^x, Com b> 0 e b ≠ 1

Onde B é uma constante real sempre positiva e diferente de 1, que é conhecida como base. Observe que a verdadeira variável x se encontra no expoente, Desta forma, f (x) é sempre um número real.

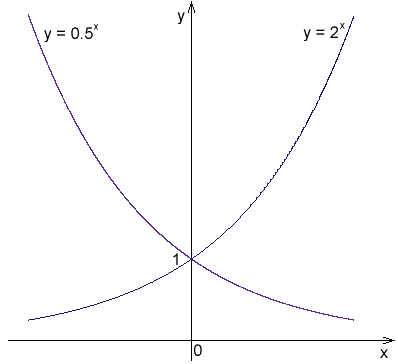figura 1. Funções exponenciais com as bases 2 e 1/2

Exemplos de funções exponenciais são os seguintes:

-f (x) = 2^x

-g (x) = 5⋅e^-3x

-H (x) = 4vid (10^2x)

Essas são funções que crescem - ou diminuem, de acordo com o sinal do expoente - muito rapidamente, então se fala do "crescimento exponencial" quando alguma magnitude aumenta muito rapidamente. É por isso que eles são apropriados para modelar o crescimento de seres vivos, como bactérias.

Outra aplicação muito interessante é a de interesse composto. Quanto mais dinheiro você tiver em uma conta, mais interesses e eles podem calcular todo o determinado intervalo de tempo, tão pequeno quanto você quiser.

Com a ajuda da função logarítmica, que é a função inversa do exponencial, pode ser conhecido após quanto tempo um determinado capital aumenta em um determinado valor.

[TOC]

Propriedades da função exponencial

Figura 2. Exemplos de funções exponenciais. Fonte: f. Zapata.

A seguir, são apresentadas as propriedades gerais de qualquer função exponencial:

-O gráfico de qualquer função exponencial sempre cruza o eixo vertical no ponto (0,1), como pode ser visto na Figura 2. Isso é porque B⁰ = 1 para qualquer valor B.

-A função exponencial não se cruza no eixo x, de fato, este eixo é uma assíntota horizontal para a função.

-Desde b¹ = b, ponto (1, b) sempre pertence aos gráficos da função.

Pode servir você: prisma hepagonal

-O domínio da função exponencial é o conjunto de números reais e f (x) = b^x É contínuo em todo o seu domínio.

-A gama de função exponencial é todos números reais maiores que 0, o que também é notado com os gráficos.

-A função exponencial é uma a uma, ou seja, cada valor x pertencente ao domínio da função, tem uma imagem única no conjunto de chegada.

-O inverso do exponencial é a função logarítmica.

Propriedades particulares da função exponencial

Como já dissemos antes, a função exponencial pode estar aumentando ou diminuindo.

Se o gráfico da Figura 2 for cuidadosamente estudado, notará que se b> 1, a função está crescendo, por exemplo y = 3^x, Mas no caso de y = (1/3)^x, com B < 1, la función decrece.

Temos dois tipos de funções exponenciais com as seguintes propriedades específicas:

Para b> 1

-A função está sempre crescendo.

-Quando o valor de B aumenta, a função cresce mais rápido, por exemplo y = 10^x cresce mais rápido que y = 2^x.

-Quando a variável é maior que 0, a função adquire valores maiores que 1, ou seja:

Para x> 0: y> 1

-E se x<0, entonces f(x) < 1.

Para b < 1

-A função está sempre diminuindo.

-Ao diminuir o valor de B, a função diminui mais rápido. Por exemplo y = (1/5)^x diminui mais rápido que y = (1/3)^x.

-Para valores de x menor que 0, a função leva valores maiores que 1, ou seja:

Para x 1

-Finalmente, quando x> 0, então e < 1.

Exemplos de funções exponenciais

A função exponencial é muito útil para modelar fenômenos em ciência e economia, como veremos abaixo:

Função exponencial natural

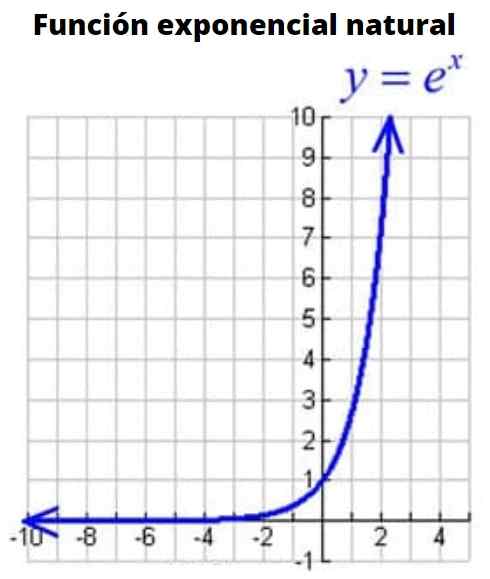Figura 3: Gráfico de função exponencial natural

É a função cuja base é o número E ou Euler, um número irracional cujo valor é:

Pode servir a você: ângulos suplementares: o que são, cálculo, exemplos, exercícios

E = 2.718181828…

Esta base, mesmo que não seja um número redondo, funciona muito bem para inúmeras aplicações. Portanto, é considerado a base mais importante de todas as funções exponenciais. A função exponencial natural é expressa de maneira matemática como:

f (x) = e^x

A função exponencial geralmente aparece em probabilidade e estatística, uma vez que várias distribuições de probabilidade, como distribuição normal, Poisson e outras, podem ser expressas através de funções exponenciais.

Interesse composto contínuo

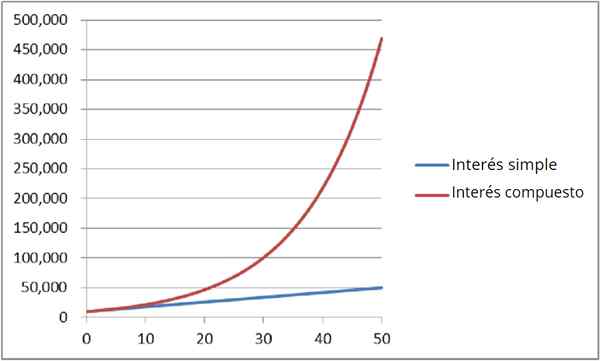Figura 4: Comparação de interesse simples e composto

Também é chamado Capitalização contínua. Para saber a quantidade de dinheiro PARA Você tem depois t anos, expressão exponencial é usada:

A (t) = p ⋅ e^Rt

Onde p é a quantidade de dinheiro originalmente depositada, r é a taxa de juros por ano e finalmente t é o número de anos.

Crescimento de bactérias

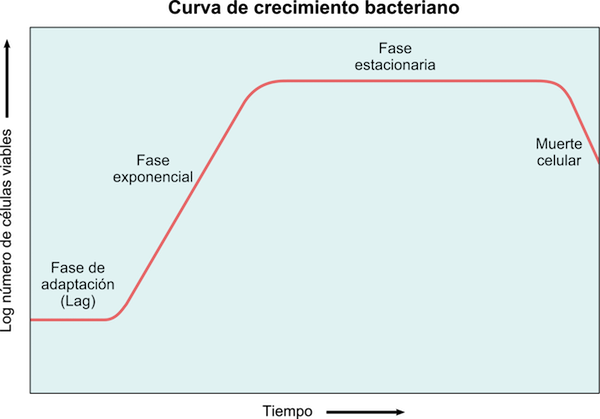Figura 5: Curva de crescimento bacteriano onde a latência, as fases exponenciais, estacionárias e de morte são observadas

As bactérias crescem exponencialmente, para que o crescimento possa ser modelado por:

N (t) = n_qualquer ⋅ e ^Kt

Onde n (t) é a população existente após o tempo t (quase sempre em horas), n_qualquer É a população inicial e k é uma constante que depende do tipo bacteriano e das condições sob as quais os nutrientes disponíveis.

Decaimento radioativo

Certos núcleos na natureza são instáveis, então eles se recusam a se transformar em mais estáveis, um processo que pode ser muito breve ou levar milhares de anos, dependendo do isótopo. Durante as partículas de decaimento radioativo, são emitidas e às vezes também fótons.

Alguns isótopos radioativos têm aplicações médicas, por exemplo, o iodo radioativo I-131, que os médicos usam no diagnóstico e tratamento de certas condições da tireóide.

O decaimento radioativo é modelado por uma função exponencial.

Pode atendê -lo: quantos décimos existem em uma unidade?

Exercícios resolvidos

As equações em que o desconhecido aparece como expoente são chamadas de equações exponenciais. Para limpar o valor do desconhecido, diferentes manipulações algébricas são usadas e o uso da função logaritmo, que é a função reversa do exponencial.

Vejamos alguns exercícios resolvidos que ilustram o ponto.

- Exercício 1

Resolva as seguintes equações exponenciais:

a 5^x = 625

b) 5^x = 2^X-1

Solução para

O número 625 é um múltiplo de 5, com efeito, ao decompuções, descobrimos que:

625 = 5⁴

Portanto, podemos escrever:

5^x = 5⁴

Como as bases são iguais à esquerda e à direita, podemos corresponder aos expoentes e obter:

x = 4

Solução b

Para este exercício, não podemos recorrer à técnica usada anteriormente, pois as bases não são as mesmas. Mas podemos aplicar logaritmo em ambos os lados da igualdade, dessa maneira:

5^x = 2^X-1

Log (5^x) = log (2^X-1)

Agora é aplicado a seguinte propriedade dos logaritmos:

Log mⁿ = n⋅Log m

E restos:

x⋅log 5 = (x-1) ⋅Log 2

x⋅ (log 5 - log 2) = -log 2

x = - log 2 ÷ (log 5 - log 2)

- Exercício 2

Indique a que função cada um dos gráficos mostrados abaixo corresponde:

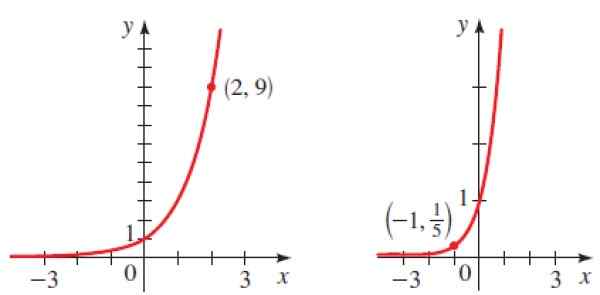Figura 6. Gráficos parest as funções exponenciais do exercício resolvido 2. Fonte: Stewart. J. Pré -cálculo.

Solução para

Como é um gráfico em crescimento, B é maior que 1 e sabemos que o ponto (2.9) pertence ao gráfico, portanto:

y = b^x → 9 = b²

Nós sabemos que 3² = 9, portanto b = 3 e a função é y = 3^x

Solução b

Novamente substituímos o ponto dado (-1, 1/5) em y = b^x para obter:

1/5 = b^-1 = 1/b

Então B = 5 e a função procurada é:

y = 5^x

Referências

1. Figuera, j. 2000. Matemática 1ª. Diversificado. Edições Co-Bo.
2. Gid Hoffmann, J. Seleção de questões de matemática para o 4º. Ano. Ed. Spphinx.
3. Jiménez, r. 2008. Álgebra. Prentice Hall.
4. Larson, r. 2010. Cálculo de uma variável. 9NA. Edição. McGraw Hill.
5. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.