Fórmulas de força centrífuga, quão calculadas, exemplos, exercícios

O força centrífuga tende a empurrar os corpos que viram uma curva. É considerado um força fictícia, Pseudofuerza qualquer força inercial, porque não é causado por interações entre objetos reais, mas é uma manifestação do inércia dos corpos. A inércia é a propriedade que faz os objetos que desejam manter o descanso ou o movimento uniforme retilíneo, se o tiver.

O termo "Força Centrífuga" foi cunhado pelo cientista Christian Huygens (1629-1695). Ele afirmou que o movimento curvilíneo dos planetas tenderia a afastá -los, a menos que o sol exercesse alguma força para retê -los e calcular que essa força era proporcional ao quadrado da velocidade e inversamente proporcional ao raio da circunferência descrita descrita.

figura 1. Ao dar uma curva, os passageiros experimentam uma força que tende a tirá -los dela. Fonte: Libreshot.

Para aqueles que viajam de carro, a força centrífuga não é fictícia. Os passageiros de um carro que se vira para a direita parecem levados para a esquerda e vice -versa, quando o carro se vira para a esquerda, as pessoas experimentam uma força à direita, que parece querer afastá -los do centro da curva.

A magnitude da força centrífuga F_g É calculado pela seguinte expressão:

 Onde:

-F_g É a magnitude da força centrífuga

-m É a massa do objeto

-v É velocidade

-R É o raio da trajetória curva.

Force é um vetor, portanto, a letra ousada é usada para distingui -la de sua magnitude, que é um escalar.

Você tem que sempre ter em mente que F_g aparece apenas quando o movimento é descrito usando um sistema de referência acelerado.

No exemplo descrito no início, o passeio que gira constitui uma referência acelerada, pois requer o aceleração centrípeta, para que eu possa virar.

[TOC]

Como a força centrífuga é calculada?

A escolha do sistema de referência é vital para a apreciação do movimento. Um sistema de referência acelerado também é conhecido como sistema não -inércia.

Nesse tipo de sistema, como um carro que gira, forças fictícias como a força centrífuga aparecem, cuja origem não é uma interação real entre objetos. Um passageiro não sabia dizer o que o empurra para fora da curva, ele só pode afirmar o que acontece assim.

Por outro lado, em um sistema de referência inercial, as interações são dadas entre objetos reais, como o corpo em movimento e a terra, o que resulta em peso, ou entre o corpo e a superfície na qual se move, que originam atrito e normal.

Um observador em pé na beira da estrada e que vê o carro para dar a curva, é um bom exemplo de sistema de referência inercial. Para este observador, o carro gira porque age uma força direcionada para o centro da curva, o que o força a não sair dela. É sobre o força centrípeta produzida por atrito entre pneus e pavimentos.

Em um sistema de referência inercial, a força centrífuga não aparece. Portanto, o primeiro passo para calculá -lo é escolher cuidadosamente o sistema de referência que será usado para descrever o movimento.

Pode servir a você: calor sensível: conceito, fórmulas e exercícios resolvidos

Finalmente, deve -se notar que os sistemas de referência inerciais não devem estar necessariamente em repouso, como o observador que olha para o veículo para dar a curva. Um sistema de referência inercial, conhecido como Estrutura de referência de laboratório, Também pode estar em movimento. Claro, com velocidade constante em relação a um inercial.

Diagrama do corpo livre em um sistema inercial e não-inequírio

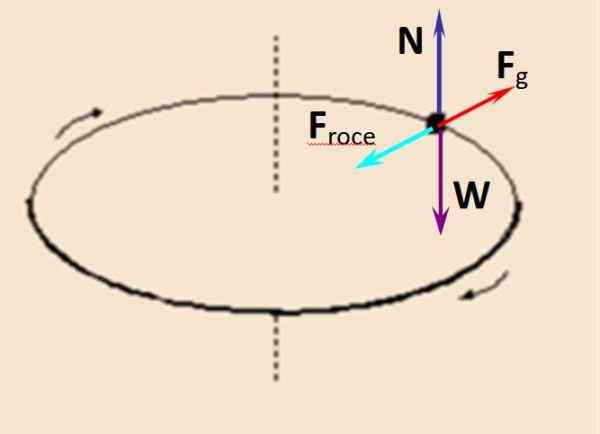
Na figura seguinte à esquerda, um observador ou está de pé e olha para O ', que está na plataforma que gira na direção indicada. Para O, que é um quadro inercial, certamente ou 'é mantido girando devido à força centrípeta F_c produzido pela parede da grade na parte de trás de O '.

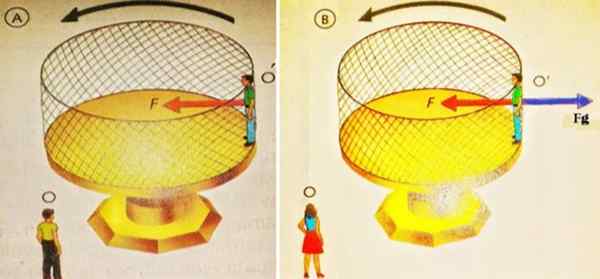Figura 2. Uma pessoa em pé em uma plataforma rotativa é vista de dois sistemas de referência diferentes: um fixo e um que acompanha a pessoa. Fonte: Santillana Physics.

Somente em sistemas de referência inercial, é válido aplicar a segunda lei de Newton, que afirma que a força líquida é igual ao produto da massa por aceleração. E, ao fazer isso, com o diagrama do corpo livre mostrado, é obtido:

F_c = ma_c

F_c= mv² / R

Da mesma forma, na figura certa, também há um diagrama de corpo livre que descreve o que o observador vê ou '. Do seu ponto de vista, ele está em repouso, portanto as forças sobre ele são equilibradas.

Essas forças são: normal F, que a parede exerce, em vermelho e direcionado para o centro e a força centrífuga F_g que o empurra para fora e que não se origina de nenhuma interação, é uma força não auditiva que aparece nos sistemas de referência em rotação.

A força centrífuga sendo fictícia, é equilibrada por uma força real, o contato ou a força normal que aponta para o centro. Portanto:

∑f_x = 0 → F_g - F = 0

F_g = F

Exemplos

Embora a força centrífuga seja considerada um pseudo -adiante, seus efeitos são bastante reais, como pode ser visto nos seguintes exemplos:

- Em qualquer jogo rotativo de um parque de diversões, a força centrífuga está presente. Ela tome cuidado para que "nós fugimos do centro" e oferece resistência constante se você tentar caminhar em direção ao centro de um carrossel em movimento. No pêndulo a seguir, você pode ver a força centrífuga:

Pode atendê -lo: Eugen Goldstein: Biografia, Contribuições e Descobertas

https: // giphy.com/gifs/jtu3pnmkqomqdujwmo

- O efeito coriolis surge da rotação terrestre, que faz com que a terra deixe de ser uma estrutura inercial. Então a força de Coriolis aparece, que uma pseudo-força que desvia lateralmente os objetos, como as pessoas que tentam andar em uma plataforma rotativa.

https: // giphy.com/gifs/the-x-files-sol-monte-funlgylkhobs

Exercícios

Exercício 1

Um carro que gira com aceleração PARA À direita, ele carrega um brinquedo de pelúcia pendurado no espelho retrovisor interno. Desenhe e compare os diagramas de corpos livres de brinquedos de:

a) o quadro de referência inercial de um observador em pé na estrada.

b) um passageiro viajando no carro.

Solução para

Um observador em pé na estrada alerta que o brinquedo se move rapidamente, com aceleração PARA para a direita.

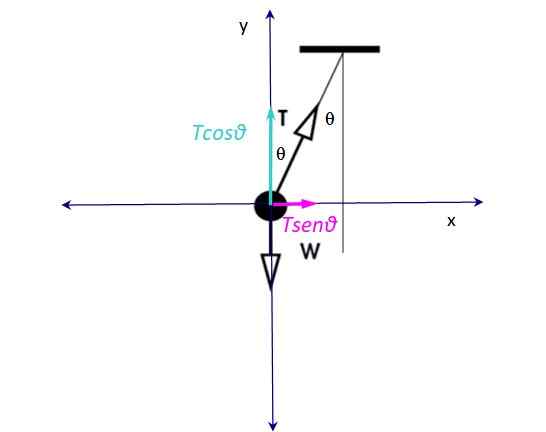Figura 3. Diagrama do corpo livre para o exercício 1A. Fonte: f. Zapata.

Existem duas forças agindo no brinquedo: por um lado, a tensão na corda T e o peso vertical abaixo C. O peso é equilibrado com o componente vertical da tensão Tcosθ, portanto:

W - tcosθ = 0

O componente horizontal da tensão: T. Senθ É a força desequilibrada responsável pela aceleração à direita; portanto, a força centrípeta é:

F_c= T.senθ = ma_c

Solução b

Para um passageiro no carro, o brinquedo fica em equilíbrio e o diagrama é o seguinte:

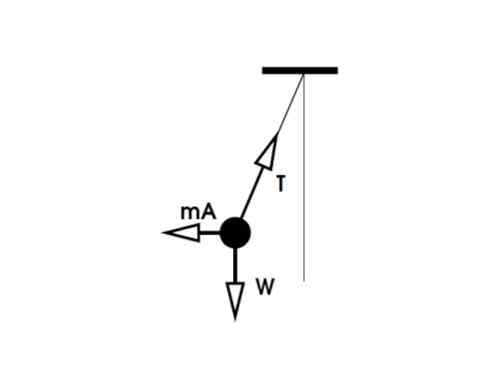Figura 4. Diagrama do corpo livre para o exercício 1b. Fonte: f. Zapata.

Como no caso anterior, o peso e o componente vertical da tensão são compensados. Mas o componente horizontal é equilibrado com força fictícia F_g = ma, de tal forma que:

-ma + tsenθ = 0

F_g = ma

Exercício 2

Uma moeda está à beira de uma antiga tarefas de vinil, cujo raio é de 15 cm e está girando a uma taxa de 33 revoluções / minuto. Encontre o coeficiente de atrito estático mínimo necessário para que a moeda seja mantida no local, usando a moeda da moeda.

Solução

Na figura está o diagrama do corpo livre para um observador que se move com a moeda. O normal N que o toadiscos exerce verticalmente para cima está se equilibrando com o peso C, Enquanto a força centrífuga F_g é compensado por esfregar estático F_tocar.

Figura 5. Diagrama do corpo livre para o exercício 2. Fonte: f. Zapata.

N - W = 0

F_tocar - F_g = 0

A magnitude da força centrífuga é MV²/R, Conforme declarado no começo, então:

F_tocar = F_g = mv²/R

Por outro lado, a força de atrito estático é dada por:

Pode atendê -lo: Volt ou Volt: conceito e fórmulas, equivalências, exemplos

F_{RECO =} μ_s.N

Onde μ_s É o coeficiente de fricção estática, uma quantidade desencadeada cujo valor depende de como as superfícies estão em contato. Substituir esta equação permanece:

μ_s.N = mv²/R → μ_s = mv²/R.N

Seria necessário determinar a magnitude do normal, que está relacionada ao peso de acordo com n = mg. Substituindo novamente:

μ_s = mv²/R.mg → μ_s = v²/Rg

De volta à declaração, isso relata que a moeda gira a uma taxa de 33 revoluções /minuto, que é velocidade angular ou frequência angular Ω, relacionado à velocidade linear v:

v = ω.R = 33 rev/min . 2π RADIANES/REV . 15 cm . (1 min/60 s) = 51. 8 cm/s

μ_s = v²/Rg = (51.8 cm/s)²/ (15cm x 981 cm/ s²) = 0.18

Os resultados deste exercício teriam sido os mesmos de ter selecionado um sistema de referência inercial. Nesse caso, a única força capaz de originar a aceleração em relação ao centro é o toque estático.

Formulários

Como temos dito, a força centrífuga é uma força fictícia, que não aparece nas estruturas inerciais, que são as únicas em que as leis de Newton são válidas. Neles, a força centrípeta é responsável por fornecer ao corpo a aceleração necessária em relação ao centro.

A força centrípeta não é uma força diferente para o já conhecido. Pelo contrário, é precisamente esses que fazem o papel das forças centrípetas quando apropriado. Por exemplo, a gravidade que faz da lua órbita.

No entanto, à medida que os sistemas de referência acelerados abundam, as forças fictícias têm efeitos muito reais. Para a amostra, aqui estão três aplicações importantes nas quais eles têm efeitos tangíveis:

Centrífugadores

Os centrífugadores são instrumentos amplamente utilizados no laboratório. A idéia é fazer uma mistura de substâncias girar em alta velocidade e essas substâncias com maior massa, experimentar maior força centrífuga, de acordo com a equação descrita no começo.

Então as partículas mais massivas tendem a se afastar do eixo de rotação, sendo assim separado do mais leve, que permanecerá mais próximo do centro.

Máquinas de lavar roupas

Máquinas de lavagem automáticas têm vários ciclos de aperto. Neles as roupas são centrifugadas para eliminar a água restante. Mais revoluções do ciclo, menos molhado serão as roupas no final da lavagem.

Curva peralte

Os carros levam melhor as curvas nas estradas, graças à estrada inclinada um pouco para o centro da curva, o que é conhecido como Peralte. Dessa maneira, o carro não depende exclusivamente do atrito estático entre os pneus e a estrada para completar a curva sem deixar a curva.

Referências

1. Acosta, Victor. Construção de um guia didático sobre força centrífuga para os alunos do Cycle v Grade 10.Recuperado de: bdigital.um i.Edu.co.
2. Toppr. Leis do movimento: circular de movimento. Recuperado de: TOPPR.com.
3. Resnick, r. (1999). Físico. Vol. 1. 3ª ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V.
4. Universidade Autônoma do Estado de Hidalgo. Força centrífuga. Recuperado de: Emirados Árabes Unidos.Edu.mx
5. Wikipedia. Centrífugadores. Recuperado de: é.Wikipedia.org.