Coeficiente de atrito viscoso (força) e exemplos

O atrito viscoso Surge quando um objeto sólido se move no meio de um gás fluido -un ou um líquido-. Pode ser modelado como uma força proporcional ao negativo da velocidade do objeto ou quadrado.

O uso de um ou outro modelo depende de certas condições, como o tipo de fluido em que o objeto é movido e se é muito rápido. O primeiro modelo é conhecido como Resistência linear, e nele a magnitude do atrito viscoso f_tocar É dado por:

F_tocar = ΓV

figura 1. Os paraqueidistas experimentam força viscosa durante sua descida, já que o ar oferece resistência. Fonte: Pixabay.

Aqui γ é a constante de proporcionalidade ou coeficiente de atrito viscoso e v é a rapidez do objeto. É aplicável a corpos que se movem em baixas velocidades de fluido com regime laminar.

No segundo modelo, conhecido como Resistência quadrática Ó Lei de Rayleight, a magnitude da força de atrito é calculada de acordo com:

F_tocar = ½ ρ.PARA.C_d.v²

Onde ρ é a densidade do fluido, a é a área transversal -seccional do objeto e C_d É o coeficiente de resistência aerodinâmica.

O produto ½ ρ.PARA.C_d  É uma aerodinâmica constante chamada D, cujas unidades são kg/m, portanto:

F_tocar = Dv²

Este modelo é mais apropriado quando a velocidade dos objetos é médio ou alta, pois o movimento produz turbulência ou redemoinhos em seu caminho no fluido.

Uma bola de tênis em movimento e os carros na rodovia são exemplos de objetos em que esse modelo funciona muito bem.

A força de viscose surge porque o sólido deve levar as camadas de fluido para poder se mover através dela. A existência de vários modelos é porque essa força depende de vários fatores, como a viscosidade do fluido, a velocidade e a forma do objeto.

Pode atendê -lo: o que é relativa permeabilidade?

Existem mais objetos aerodinâmicos do que outros e muitos são projetados com precisão para que a resistência do meio reduz sua velocidade ao mínimo.

[TOC]

Exemplos de atrito de viscose

Qualquer pessoa ou objeto que se mova em um fluido necessariamente sofra resistência ao meio ambiente, mas muitas vezes esses efeitos são desprezados por aplicações simples, como queda livre.

Nas declarações de quase todos os problemas de outono livre, note -se que os efeitos da resistência do ar se desprezam. Isso ocorre porque o ar é um fluido "fino" e é por isso que esperamos que o atrito ofereça não significativo.

Mas há outros movimentos em que o atrito viscoso tem uma influência mais decisiva, vamos ver alguns exemplos:

Pedras que caem em grãos de água e pólen

-Uma pedra que cai na vertical em um tubo cheio de petróleo experimenta uma força que se opõe à sua descida, graças à resistência a fluidos.

-Os grãos de pólen são muito pequenos; portanto, para eles a resistência do ar não é insignificante, porque graças a essa força que eles conseguem ficar à tona por um longo tempo, causando alergias sazonais.

Figura 2. Os grãos de pólen são pequenos o suficiente para que a resistência do ar tenha um efeito significativo. Fonte: Pikrepo.

Nadadores e ciclistas

-No caso dos nadadores, eles usam um chapéu e se barbeam completamente para que a resistência da água não subtraia a velocidade.

-Como os nadadores, os ciclistas em contra -relato experimentam resistência ao ar, consequentemente os capacetes têm projetos aerodinâmicos para melhorar a eficiência.

Além disso, a posição do ciclista dentro de um grupo em competição é relevante. Aquele que dirige a marcha evidentemente recebe a maior resistência do ar, enquanto para aqueles que fecham a marcha, isso é quase nulo.

Pode servir a você: Segundo Equilíbrio Condição: Explicação, Exemplos, Exercícios

Paracharidistas

-Uma vez que um paraquedista abre o pára -quedas, é exposto ao atrito viscoso do ar, sendo o modelo mais apropriado que tem o quadrado da velocidade. Dessa maneira, reduz sua velocidade e, à medida que o esfregamento se opõe à queda, atinge um valor limite constante.

Carros

-Para carros, o coeficiente de resistência aerodinâmica, uma constante que é determinada experimentalmente e a superfície que apresenta contra o vento, são os fatores determinantes para reduzir a resistência ao ar e reduzir o consumo. É por isso que eles são projetados com pára -brisas inclinados.

Experiência de queda de petróleo de Millikan

-No experimento com queda de óleo Millikan, o físico Robert Millikan estudou o movimento de gotas de óleo no meio de um campo elétrico uniforme, concluindo que qualquer carga elétrica é múltipla da carga de elétrons.

Para isso, era necessário saber o raio das gotas, que não podia ser determinado por medida direta, dado seu tamanho pequeno. Mas, neste caso. Esse fato permitiu determinar o raio das gotas e depois sua carga elétrica.

Exercícios

- Exercício 1

Na equação para força de atrito viscosa em baixa velocidade:

F_tocar = ΓV

a) Que dimensões devem o coeficiente de atrito viscoso tive γ?

b) Quais são as unidades γ no sistema internacional de unidades?

Solução para

Ao contrário dos coeficientes de atrito estáticos ou cinéticos, o coeficiente de atrito viscoso tem dimensões, que devem ser:

Pode servir a você: adesão física: o que é e exemplos

Força / velocidade

A força tem dimensões de massa x comprimento /tempo², enquanto as velocidades são de comprimento/tempo. Denotando -os da seguinte forma:

-Missa: m

-Comprimento: l

-Tempo: t

As dimensões do coeficiente de atrito viscoso γ são:

[M.L /t²] / [L / t] = [M.eu.T / l.T²] = M/t

Solução b

No SI, as unidades γ são kg/s

- Exercício 2

Levando em consideração a resistência que a água se opõe, encontrando uma expressão para a velocidade terminal de uma esferita de metal que cai na vertical em um tubo cheio de óleo, nos casos:

a) baixa velocidade

b) alta velocidade

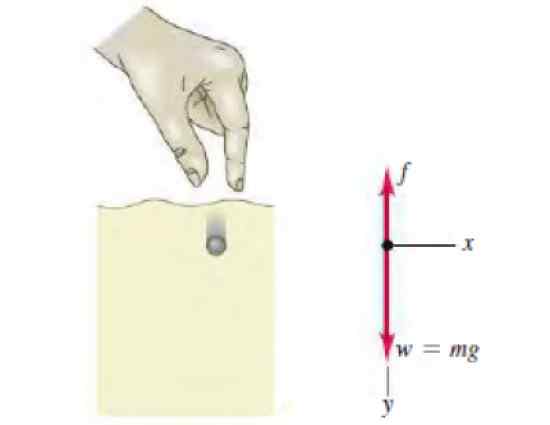Figura 3. Diagrama do corpo livre de um esferito que desce dentro de um fluido. Fonte: Sears, Z. Física da Universidade com Física Moderna.

Solução para

Na figura, o diagrama do corpo livre aparece, mostrando as duas forças que agem na esferita: o peso abaixo e a resistência do fluido, proporcional à velocidade, para cima para cima. A segunda lei de Newton para este movimento estabelece o seguinte:

γV_t - mg = 0

Onde V_t É a velocidade do terminal, dada por:

v_t = mg / γ

Solução b

Se supormos média em alta velocidade, o modelo apropriado é aquele com velocidade quadrada:

F_tocar = ½ ρ.PARA.C_d.v²

Então:

½ ρ.PARA.C_d.v² - mg = 0

D.v² - mg = 0

v = √ [mg / d]

Em ambas as situações, quanto maior a massa do objeto, maior a velocidade terminal.

Referências

1. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.
2. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1.
3. Tipler, p. (2006) Física para ciência e tecnologia. 5ª ed. Volume 1. Editorial revertido.
4. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. McGraw Hill
5. Universidade Sevilla. Forças de atrito. Recuperado de: Laplace.nós.é.