Tipos de atrito, coeficiente, cálculo, exercícios

O atrito É a resistência ao deslocamento de uma superfície enquanto em contato com outra. É um fenômeno superficial que ocorre entre materiais sólidos, líquidos e gasosos. A força de resistência tangencial a duas superfícies em contato, o que se opõe à direção do deslocamento relativo entre essas superfícies, também é chamado de força de atrito ou força de atrito F_r.

Para deslocar um corpo sólido em uma superfície, uma força externa deve ser aplicada que possa superar o atrito. Quando o corpo se move, a força de atrito age no corpo diminuindo sua velocidade e pode até impedi -lo.

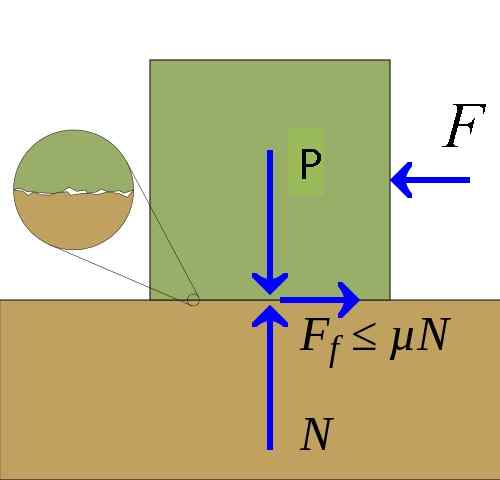
Fricção [de Keta, Pietter Kuiper (https: // Commons.Wikimedia.org/wiki/arquivo: atrito.Svg)]]

A força de atrito pode ser representada graficamente por meio do diagrama das forças de um corpo em contato com uma superfície. Neste diagrama a força de atrito F_r É desenhado pelo componente da força aplicada ao corpo tangencial à superfície.

A superfície de contato exerce uma força de reação no corpo chamado força normal N. Em alguns casos, a força normal é apenas devido ao peso P do corpo que repousa na superfície e, em outros casos, é devido a forças aplicadas além da força da gravidade.

O atrito se origina porque existem rugos microscópicos entre as superfícies em contato. Quando você tenta mover uma superfície na outra. Por sua vez, as perdas de energia são produzidas na forma de calor que não é usada para mover o corpo.

[TOC]

Tipos de atrito

Existem dois tipos principais de atrito: o atrito de Coulomb o atrito seco e atrito fluido.

-Coulomb atrito

O atrito de Coulomb Sempre se opõe ao movimento dos corpos e é subdividido em dois tipos de atrito: atrito estático e atrito cinético (ou dinâmico).

No atrito estático, não há movimento corporal na superfície. A força aplicada é muito baixa e não é suficiente para superar a força de atrito. O atrito tem um valor máximo proporcional à força normal e é chamada de força de atrito estático F_ré.

A força de atrito estático é definida como a força máxima que resiste no início do movimento do corpo. Quando a força aplicada excede a força de atrito estático, ela permanece no seu valor máximo.

O atrito cinético age quando o corpo está em movimento. A força necessária para manter o corpo com atrito é chamado de força de atrito cinético F_Rc.

A força de atrito cinético é menor ou igual à força de atrito estático, porque uma vez que o corpo começa a se mover, é mais fácil continuar movendo -o do que tentar fazê -lo enquanto está em repouso.

Leis de atrito de Coulomb

1. A força de atrito é diretamente proporcional à força normal para a superfície de contato. A constante de proporcionalidade é o coeficiente de atrito μ que existe entre as superfícies em contato.
2. A força de atrito é independente do tamanho da aparente área de contato entre as superfícies.
3. A força de atrito cinético é independente da velocidade de deslizamento do corpo.

-Fricção fluida

O atrito também ocorre quando os corpos se movem em contato com materiais líquidos ou gasosos. Esse tipo de atrito é chamado de atrito de fluido e é definido como a resistência ao movimento de corpos em contato com um fluido.

Pode atendê-lo: Experiências de física fácil (Universidade Primária)

O atrito do fluido também se refere à resistência de um fluido para fluir em contato com camadas de fluido do mesmo material ou diferente, e depende da velocidade e da viscosidade do fluido. A viscosidade é a medida de resistência ao movimento de um fluido.

-Stokes atrito

O atrito de Stokes é um tipo de atrito de fluido, no qual partículas esféricas imersas em um fluido viscoso, no fluxo laminar, experimentam uma força de atrito que diminui seu movimento devido às flutuações das moléculas de fluido.

Stokes Friction [por Kraaiennest (https: // Commons.Wikimedia.org/wiki/arquivo: Stokes_sphere.Svg)]]

O fluxo é laminar quando as forças viscosas, que se opõem ao movimento do fluido, são maiores que as forças inerciais e o fluido se move com velocidade suficientemente pequena e em trajetória retilínea.

Coeficientes de atrito

De acordo com a primeira lei de atrito de Coulomb O coeficiente de atrito μ É obtido da relação entre força de atrito e força normal à superfície de contato.

μ = f_r/N

O coeficiente μ É uma quantidade adimensional, porque é uma relação entre duas forças, o que depende da natureza e do tratamento de materiais em contato. Geralmente o valor do coeficiente de atrito está entre 0 e 1.

Coeficiente de atrito estático

O coeficiente de atrito estático é a constante de proporcionalidade que existe entre a força que impede o movimento de um corpo em um estado de contato em uma superfície de contato e a força normal para a superfície.

μ_e= F_ré/N

Coeficiente de atrito cinético

O coeficiente de atrito cinético é a constante de proporcionalidade que existe entre a força que restringe o movimento de um corpo que se move em uma superfície e a força normal para a superfície.

μ_c= F_Rc/N

O coeficiente de atrito estático é maior que o coeficiente de atrito cinético.

μ_S> μ_c

Coeficiente de atrito elástico

O coeficiente de atrito elástico deriva do atrito entre as superfícies de contato de materiais elásticos, macios ou ásperos que são deformados pelas forças aplicadas. O atrito se opõe ao movimento relativo entre duas superfícies elásticas e o deslocamento é acompanhado por uma deformação elástica das camadas superficiais do material.

O coeficiente de atrito obtido nessas condições depende do grau de rugosidade da superfície, nas propriedades físicas dos materiais de contato e na magnitude do componente tangencial da força de ouvir na interface material.

Coeficiente de atrito molecular

O coeficiente de atrito molecular é obtido da força que restringe o movimento de uma partícula que desliza em uma superfície macia ou através de um fluido.

Como o atrito é calculado?

A força de atrito em interfaces sólidas é calculada usando a equação F_r = μn

N É a força normal e μ É o coeficiente de atrito.

Em alguns casos, a força normal é igual ao peso do corpo P. O peso é obtido multiplicando a massa m do corpo devido à aceleração da gravidade g.

P= mg

Ao substituir a equação de peso na equação da força de atrito, é obtido:

Pode atendê -lo: aceleração média: como é calculado e resolvido

F_r = μmg

Características normais

Quando um objeto está em repouso em uma superfície plana, a força normal é a que exerce a superfície no corpo e se opõe à força devido à gravidade, de acordo com a Lei de Ação e Ação de Newton.

A força normal sempre age perpendicular à superfície. Em uma superfície inclinada, o normal diminui à medida que o ângulo de inclinação aumenta e aponta na direção perpendicular para longe da superfície, enquanto o peso aponta verticalmente para baixo. A equação de força normal em uma superfície inclinada é:

N = mgcosθ

θ = ângulo de inclinação da superfície de contato.

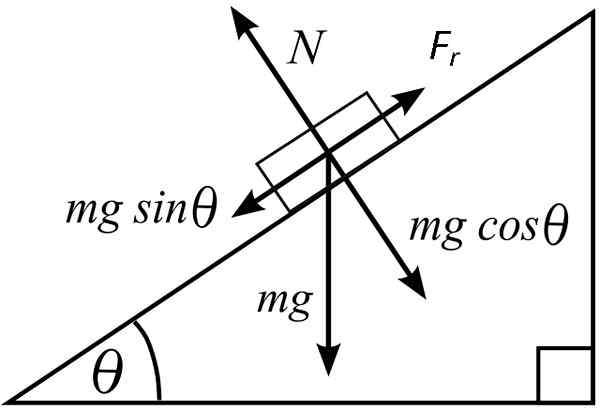Fricção no plano inclinado [pelo Mets501 (https: // commons.Wikimedia.org/wiki/arquivo: free_body.Svg)]]

O componente da força que atua no corpo para deslizar é:

F = mgsenθ

À medida que a força aplicada aumenta para o valor máximo da força de atrito, esse valor corresponde à força de atrito estático. Quando  F = f_ré, A força de atrito estático é:

F_ré= mgsenθ

E o coeficiente de atrito estático é obtido por tangente do ângulo de inclinação θ.

μ_e = tanθ

Exercícios resolvidos

-Força de atrito de um objeto que repousa em uma superfície horizontal

Uma caixa de 15 kg colocada em uma superfície horizontal é empurrada por uma pessoa que aplica uma força de 50 Newton ao longo de uma superfície para se mover e depois aplicar uma força 25 N para manter a caixa em movimento a uma velocidade constante. Determinar coeficientes de atrito estáticos e cinéticos.

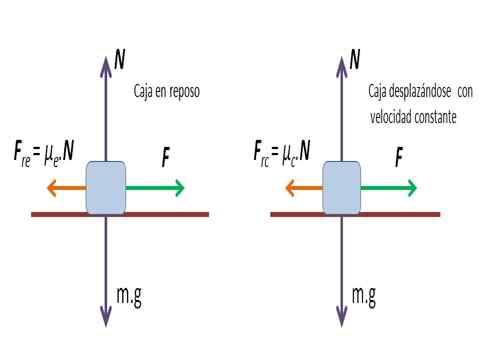Caixa movendo -se na superfície horizontal

Solução: Com o valor da força aplicada para mover a caixa, o coeficiente de atrito estático é obtido μ_e.

μ_e= F_ré/N

A força normal N para a superfície é igual ao peso da caixa, então N = m.g

N = 15kgx9,8m/s²

N = 147New

Neste caso, μ_e= 50New/147New

μ_e= 0,34

A força aplicada para manter a velocidade da caixa constante é a força de atrito cinético que é igual a 25New.

O coeficiente de atrito cinético é obtido com a equação μ_c= F_Rc /N

μ_c= 25New/147New

μ_c= 0,17

-Força de atrito de um objeto sob a ação de uma força com um ângulo de inclinação

Um homem aplica uma força a uma caixa de 20 kg, com um ângulo de aplicação de 30 ° em relação à superfície onde ele descansa. Qual é a magnitude da força aplicada para mover a caixa se o coeficiente de atrito entre a caixa e a superfície for 0,5?

Solução: a força aplicada e seus componentes verticais e horizontais são representados no diagrama do corpo livre.

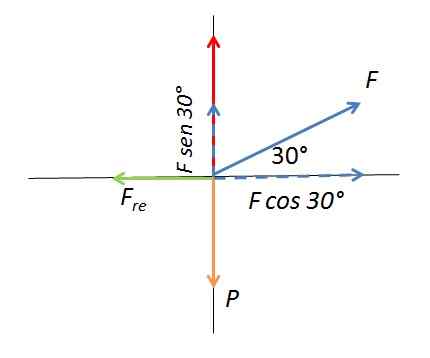Diagrama de corpo livre

A força aplicada forma um ângulo de 30 ° com a superfície horizontal. O componente vertical da força aumenta a força normal que afeta a força de atrito estático. A caixa se move quando o componente horizontal da força aplicada excede o valor máximo da força de atrito F_ré. Ao combinar o componente horizontal da força com o de atrito estático, é obtido:

F_ré = Fcosθ                       [1]

F_ré= μ_e.N                          [2]

Pode atendê -lo: Rutherford Atomic Model: History, Experimentos, Postula

μ_e.N = fCOSθ                      [3]

força normal

A força normal não é mais o peso do corpo devido ao componente vertical da força.

De acordo com a segunda lei de Newton, a soma das forças que atuam na caixa no eixo vertical é nulo, portanto o componente vertical da aceleração é para_e= 0. A força normal é obtida da soma

F sen30 ° + n - p = 0                      [4]

P = m.g                                        [5]

F SNN 30 ° + N - M.G = 0                [6]

N = m.G - f sen 30 °                      [7]

Ao substituir a equação [7] na equação [3], é obtido o seguinte:

μ_e. (m.G - f sin 30 °) = fCOS30 °     [8]

Isso limpa F Da equação [8] e obtido:

F = μ_e . m.G /(cos 30 ° + μ_e sin 30 °) = 0,5 x 20kg x 9,8m/s² / (0,87+ (0,5 x 0,5)) =

F = 87.5New

-Fricção em um veículo em movimento

Um veículo de 1,5 toneladas se move em uma estrada retilínea e horizontal a uma velocidade de 70 km/h. O motorista visualiza, a uma certa distância, obstáculos na estrada que o forçam a parar bruscamente. Depois de parar o veículo de skate por um breve período de tempo até parar. Se o coeficiente de atrito entre os pneus e a estrada for de 0,7; Determine o seguinte:

1. Qual é o valor do atrito enquanto o veículo da pátina?
2. Desaceleração do veículo
3. A distância percorrida pelo veículo para para parar.

Solução:

Seção a

O diagrama do corpo livre mostra as forças que atuam no veículo ao patinar.

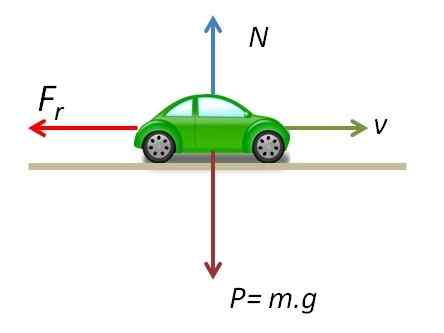Forças agindo em um veículo em movimento

Como a soma das forças que atuam no eixo vertical é zero, a força normal é igual ao peso do veículo.

N = m.g

M = 1,5 ton = 1500kg

N = 1500kgx9,8m/s²= 14700New

A força de atrito do veículo quando o patinação é:

F_r = μn = 0,7x14700New

= 10290 NOVO

Seção b

A força de atrito influencia a diminuição da velocidade do veículo ao patinar.

Ao aplicar a segunda lei de Newton, o valor da desaceleração é obtido limpando a equação F = m.para

A = f/m

a = (-10290 novo)/ 1500kg

= -6,86m/s²

Seção c

A velocidade inicial do veículo é v₀ = 70 km/h = 19,44m/s

Quando o veículo parar sua velocidade final, é v_F = 0 E a desaceleração é a = -6,86m/s²

A distância percorrida pelo veículo, pois ele para até que ele pare, é obtido pela limpeza d da seguinte equação:

v_F² = v₀²+2ad

D = (V_F² - v₀²)/2a

= ((0)²-(19,44m/s)²)/(2x (-6,86m/s²)

D = 27,54m

O veículo viaja 27,54m distância antes de parar.

 Referências

1. Cálculos do coeficiente de atrito sob condições de contato elásticas. Mikhin, n m. 2, 1968, Soviet Materials Science, vol. 4, p. 149-152.
2. Blau, p j. Ciência e tecnologia de atrito. Florida, EUA: CRC Press, 2009.
3. Relação entre adesão e forças de atrito. Isralachvili, J n, Chen, você-pulmão e Yoshizawa, H. 11, 1994, Journal of Adhesion Science and Technology, vol. 8, p. 1231-1249.
4. Zimba, J. Força e movimento. Baltimore, Maryland: The Johns Hopkins University Press, 2009.
5. Bhushan, b. Princípios e aplicações de tribologia. Nova York: John Wiley e Sons, 1999.
6. Sharma, C S e Purohit, K. Teoria dos mecanismos e máquinas. Nova Délhi: Prentice Hall of India, 2006.