Fluxo volumétrico

Explicamos o que é o fluxo volumétrico, como calculá -lo e os fatores que o afetam

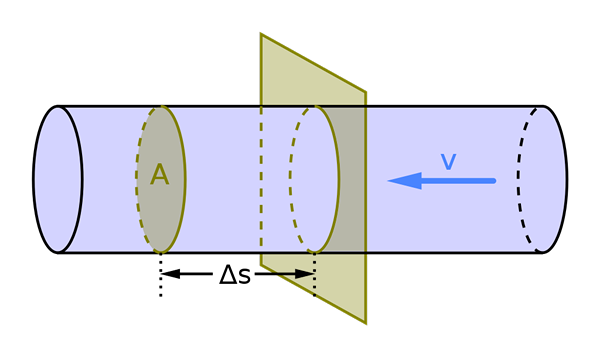
O fluxo volumétrico depende da área da seção transversal e da velocidade do fluido V. Fonte: Mikerun, CC BY-SA 4.0, via Wikimedia Commons

O que é fluxo volumétrico?

Ele fluxo volumétrico Ele permite determinar o volume de fluido que atravessa uma seção do duto e oferece uma medida de velocidade com que o fluido se move pelo mesmo. Portanto, sua medida é especialmente interessante em áreas tão diversas quanto a indústria, medicina, construção e pesquisa, entre outros.

No entanto, medir a velocidade de um fluido (um líquido, um gás ou uma mistura de ambos) não é tão simples quanto a velocidade de deslocamento de um corpo sólido pode ser medir. Portanto, acontece que saber a velocidade de um fluido, é necessário conhecer seu fluxo.

A partir disso e de muitas outras questões relacionadas a fluidos, o ramo da física conhecida como oferta de mecânica de fluidos. O fluxo é definido como o fluido de uma seção de um duto, já é um oleoduto, um oleoduto, um rio, um canal, uma corrente sanguínea, etc., Levando em consideração uma unidade temporária.

Geralmente é calculado o volume em que uma certa área em uma unidade de tempo é calculada, também chamada de fluxo volumétrico. O fluxo de massa ou massa que atravessa uma área determinada em um horário específico também é definido, embora seja usado com menos frequência do que o fluxo volumétrico.

Como é calculado o fluxo volumétrico?

O fluxo volumétrico é representado pela letra q. Para os casos em que o fluxo se move perpendicularmente para a seção do motorista, ele é determinado com a seguinte fórmula:

Q = a = v / t

Nesta fórmula A é a seção do motorista (é a velocidade média que o fluido tem), v é o volume e o tempo t. Como no sistema internacional a área ou seção do motorista é medida em m² E a velocidade em m/s, o fluxo é medido m³/s.

Pode atendê -lo: 21 eventos importantes da física

Para os casos em que a velocidade do deslocamento do fluido cria um ângulo θ com a direção perpendicular à seção da superfície A, a expressão para determinar o fluxo é a seguinte:

Q = A cos θ

Isso é consistente com a equação anterior, pois quando o fluxo é perpendicular à área A, θ = 0 e, portanto, cos θ = 1.

As equações acima são verdadeiras se a velocidade do fluido for uniforme e se a seção da seção for plana. Caso contrário, o fluxo volumétrico é calculado através da seguinte integral:

Q = ∫∫_s v d s

Neste DS integral, é o vetor de superfície, determinado pela seguinte expressão:

Ds = n ds

Lá, n é o vetor de unidade normal para a superfície do duto e DS um elemento de superfície diferencial.

Equação de continuidade

Uma característica dos fluidos incompressíveis é que a massa do fluido é preservada por meio de duas seções. É por isso que a equação de continuidade é cumprida, que estabelece o seguinte relacionamento:

ρ₁ PARA₁ V₁ = ρ₂ PARA₂ V₂

Nesta equação ρ é a densidade do fluido.

Para casos de regimes em fluxo permanente, no qual a densidade é constante e, portanto, é cumprida que ρ₁ = ρ₂, É reduzido à seguinte expressão:

PARA₁ V₁ = A₂ V₂

Isso é equivalente a afirmar que o fluxo é preservado e, portanto,:

Q₁ = Q₂.

A partir da observação do exposto, segue -se que os fluidos aceleram quando atingem uma seção mais estreita de um duto, enquanto reduzem sua velocidade quando atingem uma seção mais ampla de um duto. Esse fato tem aplicações práticas interessantes, pois permite brincar com a velocidade de deslocamento de um fluido.

Pode atendê -lo: partículas subatômicas

Princípio de Bernoulli

O princípio de Bernoulli determina que, para um fluido ideal (ou seja, um fluido que não tem viscosidade ou atrito) que se move em um regime de circulação através de um duto fechado é cumprido que sua energia permanece constante em todo o seu deslocamento.

Por fim, o princípio de Bernoulli não é nada além da formulação da lei de conservação de energia para o fluxo de um fluido. Assim, a equação de Bernoulli pode ser formulada da seguinte maneira:

H +v² / 2g+p/ ρg = constante

Nesta equação h é a altura e g é a aceleração da gravidade.

Na equação de Bernoulli, a energia de um fluido é levada em consideração a qualquer momento, energia que consiste em três componentes.

• Um componente cinético que inclui energia, devido à velocidade com que o fluido se move.
• Um componente gerado pelo potencial gravitacional, como conseqüência da altura em que o fluido está localizado.
• Um componente da energia de fluxo, que é a energia que um fluido tem devido à pressão.

Nesse caso, a equação de Bernoulli é expressa da seguinte maneira:

H ρ g +(v² ρ)/2 + p = constante

Logicamente, no caso de um fluido real, a expressão da equação de Bernoulli não é cumprida, pois no deslocamento do fluido há perdas de atrito e é necessário recorrer a uma equação mais complexa.

O que afeta o fluxo volumétrico?

O fluxo volumétrico será afetado se houver uma obstrução no duto.

Pode servir a você: refração leve: elementos, leis e experimentos

Além disso, o fluxo volumétrico também pode mudar pelo efeito da temperatura da temperatura e da variação da pressão e pela pressão para a qual é.

Método simples de medir o fluxo volumétrico

Um método realmente simples para medir o fluxo volumétrico é deixar um fluido fluir dentro de um tanque de medição por um certo período de tempo.

Esse método geralmente não é muito prático, mas a verdade é que é extremamente simples e muito ilustrativo entender o significado e a importância de conhecer o fluxo de um fluido.

Dessa maneira, o fluido pode fluir para um tanque de medição por um período de tempo, o volume acumulado é medido e o resultado obtido entre o tempo decorrido é dividido.

Referências

1. Fluxo (fluido) (n.d.).  Na Wikipedia. Recuperado de es.Wikipedia.org.
2. Taxa de fluxo volumétrica (n.d.).  Na Wikipedia. Recuperado de.Wikipedia.org.
3. Engenheiros Edge, LLC. "Equação de vazão volumétrica de fluido". Engenheiros de borda
4. Mott, Robert (1996). "1". Mecânica de fluido aplicado (4ª edição). México: Pearson Education.
5. Batchelor, g.K. (1967). Uma introdução à dinâmica fluida. Cambridge University Press.
6. Landau, l.D.; Lifshitz, e.M. (1987). Mecânica de fluidos. Curso da física teórica (2ª ed.). Pergamon Press.