Esforço normal do que consiste, como é calculado, exemplos

Ele esforço normal Aplicado a um determinado material, também chamado de esforço uniaxial, é a relação entre a força aplicada perpendicularmente a uma certa superfície e a área transversal -seccional na qual atua, ou a carga por unidade de área. Matematicamente, se p é a magnitude da força e a é a área onde é aplicada, o esforço σ é o quociente: σ = p/a.

As unidades de esforço normal no sistema internacional são Newton /Metro², conhecido como Pascal e PA abreviado. Estas são as mesmas unidades de pressão. Outras unidades que aparecem na literatura são frequentemente libras / polegadas² qualquer psi.

figura 1. As rochas são constantemente submetidas a esforços devido à atividade tectônica, causando deformações na crosta terrestre. Fonte: Pixabay.

Na Figura 2, duas forças de igual magnitude são aplicadas perpendicularmente à área transversal -seccional, fazendo uma tração na barra de luz que tende a estendê -la.

Essas forças produzem um esforço normal que também é chamado Carga axial centrado, porque sua linha de ação coincide com o eixo axial, no qual o centróide está localizado.

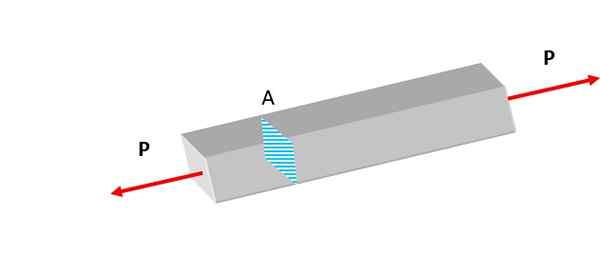Figura 2. A barra mostrada está sujeita a forças de tração. Fonte: Self feito.

Esforços, normais ou outros tipos, aparecem continuamente na natureza. Na litosfera, as rochas estão sujeitas a gravidade e atividade tectônica, experimentando deformações.

Dessa maneira, estruturas como dobras e falhas se originam, cujo estudo é importante no uso de minerais e engenharia civil, para a construção de edifícios e estradas, para citar alguns exemplos.

[TOC]

Como é calculado?

A equação dada no início σ = p/a permite calcular o esforço médio normal na área em questão. O valor de P é a magnitude da força resultante sobre a área aplicada ao centróide e é suficiente para muitas situações simples.

Nesse caso, a distribuição de forças é uniforme, especialmente em pontos de distância de onde você tem o bar sujeito a tração ou compressão. Mas se o esforço for necessário para calcular em um ponto específico ou as forças não forem distribuídas uniformemente, é necessário usar a seguinte definição:

Pode atendê -lo: circuito elétrico fechado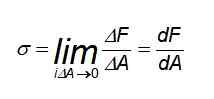

Então, em geral, o valor do esforço em um determinado ponto pode ser diferente do valor médio. De fato, o esforço pode variar de acordo com a seção a considerar.

Isso é ilustrado na figura a seguir, na qual as forças de tração f tentam separar a barra em equilíbrio nas seções milímetros e nn.

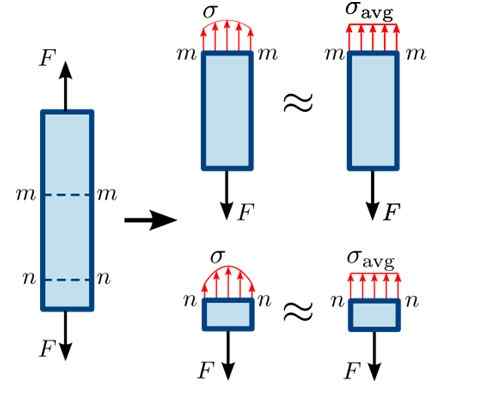Figura 3. Distribuição de esforços normais em diferentes seções de um bar. Fonte: https: // Commons.Wikimedia.org/wiki/arquivo: Normal_stress.Svg#/mídia/arquivo: normal_stress.Svg

Como a seção nn É muito próximo de onde a força F down, a distribuição de forças na superfície não é totalmente homogênea, sendo esses menores que são mais distantes daquele ponto. A distribuição é um pouco mais homogênea na seção milímetros.

De qualquer forma, o esforço normal sempre tende a esticar ou comprimir as duas partes do corpo que são encontradas em ambos. Por outro lado, outros esforços diferentes, como cisalhamento, tendem a se mover e separar essas partes.

Lei de Hooke e esforço normal

A lei de Hooke afirma que, dentro dos limites elásticos, o esforço normal é diretamente proporcional à deformação experimentada pela barra ou objeto. Em tal caso:

Esforço normal ∝ Deformação unitária

A constante de proporcionalidade é o módulo jovem (y):

Esforço normal (σ) = módulo jovem (y) x deformação unitária (ε)

σ = y. ε

Com ε = ΔL/L, onde ΔL é a diferença entre o comprimento final e o inicial, que é l.

O módulo jovem ou módulo de elasticidade é uma característica do material, cujas dimensões são as mesmas que as do esforço, uma vez que a deformação da unidade é adimensional.

Pode servir a você: 13 exemplos da segunda lei de Newton na vida cotidiana

Importância do esforço na resistência de materiais e geologia

Determinar quão resistentes são os materiais para os esforços é muito importante. Para as estruturas usadas na construção de edifícios, bem como no design de peças para diferentes dispositivos, é necessário garantir que os materiais escolhidos cumpram adequadamente sua função.

Portanto, os materiais são analisados ​​exaustivamente em laboratórios por meio de ensaios destinados a saber quanta força eles podem resistir antes de deformar e quebrar, perdendo assim suas funções. Com base nisso, é tomada a decisão de fabricar ou não uma determinada peça ou fazer parte de um dispositivo.

Acredita -se que o primeiro cientista a estudar sistematicamente a resistência dos materiais foi Leonardo da Vinci. Ele deixou evidências de ensaios em que determinou a resistência de fios pendurados em pedras de diferentes pesos.

Nos esforços, a magnitude da força e também as dimensões da estrutura e como ela é aplicada é importante, a fim de estabelecer os limites dentro dos quais o material tem um comportamento elástico; isto é, ele retorna à sua forma original quando o esforço cessa.

Com os resultados desses testes, as curvas de deformação do esforço são realizadas para diferentes tipos de materiais, como aço, concreto, alumínio e muito mais.

Exemplos

Nos exemplos a seguir, supõe -se que as forças sejam distribuídas uniformemente e que o material é homogêneo e isotrópico. Isso significa que suas propriedades são as mesmas em qualquer direção. Portanto, é válido aplicar a equação σ = p/a para encontrar esforços.

-Exercício 1

Na Figura 3, sabe -se que o esforço normal médio que atua na seção AB tem magnitude 48 kPa. Encontre: a) A magnitude da força f que age em CB, b) o esforço na seção BC.

Pode atendê -lo: tiro horizontal: características, fórmulas e equações, exercícios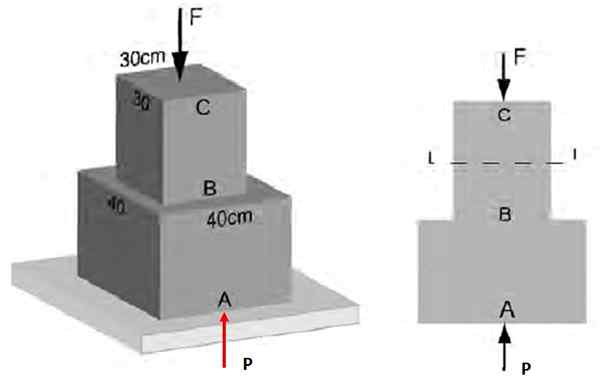Figura 4. Esforços normais na estrutura do Exemplo 1 ..

Solução

Como a estrutura está em equilíbrio estático, de acordo com a segunda lei de Newton:

P-f = 0

O esforço normal na seção AB tem magnitude:

σ_Ab = P/A_Ab

Onde p = σ_Ab . PARA_Ab = 48000 PA. (40 x 10 ^-2 m)² = 7680 n

Portanto f = 7680 n

O esforço normal na seção BC é a razão entre a magnitude de F e a área da seção transversal desse lado:

σ_Bc = F/a_Bc = 7680 n / (30 x 10 ^-2 m)² = 85.3 KPa.

-Exercício 2

Um fio de 150 m de comprimento e 2.5 mm de diâmetro é esticado por uma força de 500 N. Encontrar:

a) esforço longitudinal σ.

b) Deformação unitária, sabendo que o comprimento final é 150.125 m.

c) o módulo de elasticidade E deste fio.

Solução

a) σ = f / a = f / π.r²

O raio do fio é metade do diâmetro:

R = 1.25 mm = 1.25 x 10^-3 m.

A área de seção cruzada é π.r², Então o esforço é:

σ = f / π.r² = 500 / (π.(1.25 x 10^-3)² PA = 101859.2 Pa

b) ε = ΔL / l = (comprimento final - comprimento inicial) / comprimento inicial

Portanto:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) O módulo do jovem do fio é limpo ao conhecer os valores de ε e σ calculados anteriormente:

Y = σ / ε = 101859.2 pa / 0.000833 = 1.22 x 10⁸ PA = 122 MPA.

Referências

1. Cerveja, f. 2010. Mecânica de Materiais. 5 ª. Edição. McGraw Hill. 7 - 9.
2. Giancoli, d.  2006. Física: Princípios com aplicações. 6^tº  Ed. Prentice Hall. 238-242.
3. Hibbeler, R.C. 2006. Mecânica de Materiais. 6º. Edição. Pearson Education. 22 -25
4. Valera Negrete, J. 2005. Notas de física geral. Unam. 87-98.
5. Wikipedia. Estresse (mecânica). Recuperado de: Wikipedia.org.