Em que situações são funções lineares e quadráticas?

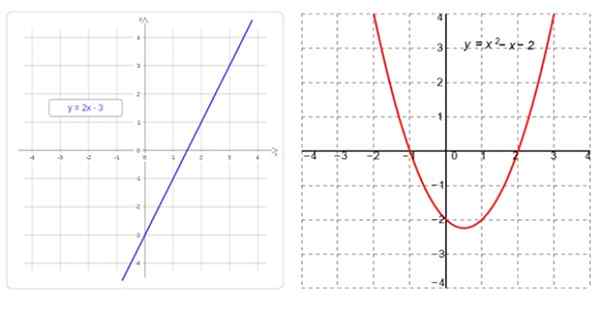
À esquerda, uma função linear, cujo gráfico é uma linha reta e, à direita, uma função quadrática, cujo gráfico é uma parábola. Fonte: f. Zapata

O que são funções lineares e quadráticas?

Funções lineares e funções quadráticas são funções que pertencem ao grupo de funções polinômicas. Eles são usados ​​para modelar várias situações, como a dependência entre o volume e o peso de um corpo, a quantidade e o custo de um produto, a posição versus o tempo e mais.

Em geral, uma função é um relacionamento que vincula duas variáveis ​​e pode ser usado para modelar o mundo real. As funções polinômicas, como o nome indica, são expressas através de um polinômio, cuja forma geral é:

f (x) = a_nxⁿ + para _N-1x ^N-1 + para_X-2x^N-2 +… para_qualquer

Onde n é um número natural, os números para₀, para₁, para₂,… para_n Eles são reais, para₀ É o termo independente e para_n, É o coeficiente que acompanha a maior potência. O valor de n indica o tipo de função, para n = 1 a função é linear, enquanto para n = 2 a função é quadrática.

No primeiro desses casos, a expressão geral é reduzida a:

f (x) = a₁x + a_qualquer

E no segundo caso, permanece assim:

f (x) = a₂x² + para₁x + a_qualquer ;   (para₂≠ 0)

Os gráficos das funções polinomiais são contínuos, ou seja, eles não experimentam saltos ou rupturas abruptas, com comportamento suave, sem irregularidades. Portanto, eles são observados na modelagem de muitas situações de ciência, economia e outras áreas do conhecimento humano.

Em seguida, aplicações interessantes uma da outra são descritas em mais detalhes.

Situações em que as funções lineares aparecem

A função linear é representada algebraicamente por:

f (x) = a₁x + a_qualquer

Ou equivalente:

f (x) = mx + b

Sua característica distinta é que seu gráfico é uma linha reta. O valor m, qual é o coeficiente do x, representa o brinco desta linha e dá uma medida de quão inclinado é.

Pode atendê -lo: programação não linear: métodos e exercícios

A inclinação pode ser positiva, negativa ou zero, mas é sempre constante, ou seja, sua taxa de câmbio permanece inalterada.

Uma linha de inclinação 0 é totalmente horizontal, a de inclinação positiva indica elevação ou aumento (se uma das variáveis ​​aumentar, a outra também, sempre na mesma taxa) e, finalmente, a inclinação negativa indica diminuição (como a das variáveis aumenta, o outro diminui).

O valor de b, Por sua parte, representa o corte ou interseção da linha com o eixo vertical. Sim B = 0, A linha passa pela origem do sistema de coordenadas.

Exemplos de modelagem com funções lineares

1. O movimento retilíneo uniforme

A equação que vincula a posição x e o tempo t de um celular, no movimento uniforme retilíneo, é linear:

x (t) = vinal + x_qualquer

Onde V, a inclinação da linha, é a velocidade do celular, que permanece constante em todo o movimento, e x_qualquer é a posição inicial.

2. Densidade

Densidade de um objeto ou substância, que estabelece a relação entre massa e volume. Chamando ρ para a densidade (ela diz "Rho"), M à massa e V para o volume, você tem:

Limpando a massa, em termos de volume, é obtido:

M = ρv

Ao representar graficamente a massa, dependendo do volume, é obtida uma linha reta cuja inclinação é a densidade do objeto ou substância.

3. Comprimento de uma circunferência

O contorno de um círculo, ou seu comprimento, é proporcional ao seu raio. Isso significa que quanto maior o raio, maior o contorno da circunferência, de acordo com a equação:

Pode servir a você: coeficiente de correlação: fórmulas, cálculo, interpretação, exemplo

C = 2πr

Onde C é o contorno ou comprimento, r é o rádio e π (lê “pi”) é uma constante cujo valor aproximado é πamp3.14 ..

4. Custo de enviar um pacote

Como é fácil de deduzir, mais pesado ou volumoso é um pacote mais caro é transportá -lo. Empresas dedicadas ao transporte de carga modelam seus preços seguindo certas regras, por exemplo:

C (x) = 2.75x

Nesta equação, C (x) é o custo do dólar para enviar um pacote cujo peso é x libras. O valor constante 2.75 possui unidades de dólar/libra (custo unitário).

Situações em que as funções quadráticas aparecem

Algebricamente, uma função quadrática é representada por:

f (x) = a₂ x² + para₁ x + a_qualquer

Com a condição de que o coeficiente de₂ Ser diferente de 0. É caracterizado por seu gráfico em forma de parábola, cujo eixo axial ou eixo de simetria é vertical (paralelo ao eixo y)).

A interseção entre o parábola e o referido eixo é um ponto chamado vértice. Se a parábola se abrir (um₂ > 0), o vértice é o seu ponto mínimo e se abrir₂ < 0), es el máximo.

No eixo da simetria está o foco, um ponto especial que determina a curvatura da parábola. Se a luz solar for influenciada em um espelho parabólico, os raios serão refletidos na superfície, coincidindo no foco, que é aquecido imediatamente.

Exemplos de modelagem com funções quadráticas

1. A altura de um projétil foi lançado verticalmente

Um projétil é qualquer objeto ao qual uma velocidade inicial é fornecida e depois liberada, sob a ação da gravidade. Se a velocidade inicial for vertical, magnitude v₀ e direcionado, o objeto subirá para uma altura máxima e depois descerá.

Pode atendê -lo: homotecia

A equação da altura h em função do tempo t é:

H (t) = −4.9 t²+v₀ t

Onde o sentido vertical é considerado positivo e o vertical negativo.

2. A trajetória de um projétil horizontal ou oblíqua

Se uma velocidade inicial horizontal ou oblíqua for fornecida a um projétil, ele descreverá uma trajetória parabólica, que pode ser representada através de uma função quadrática como descrito anteriormente.

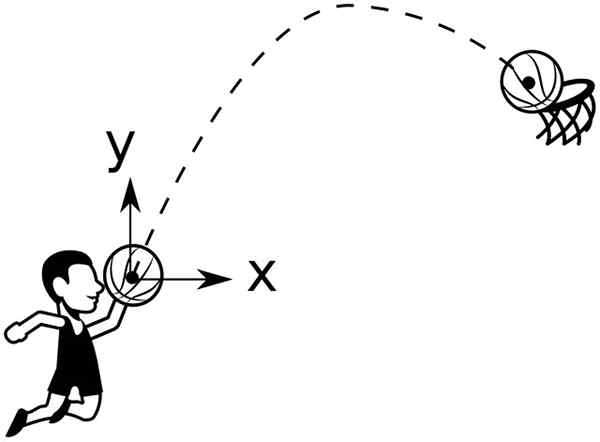A bola da cesta descreve uma trajetória parabólica a ser jogada na cesta. Fonte: Wikimedia Commons

Por exemplo, uma bola jogada de uma altura e₀, formando ângulo θ₀ Em relação ao horizontal, ele tem uma trajetória dada por:

Com g como a aceleração da gravidade, que pode aproximar 10 m/s². Por exemplo, uma bola de futebol chute do chão (e₀ = 0), com velocidade inicial de 6 m/se ângulo de 45º em relação à horizontal, terá uma trajetória dada pela seguinte parábola:

3. A área de um círculo

Quanto maior o raio do círculo, maior será sua área. De fato, a área do círculo é proporcional ao quadrado do raio r, sendo a constante da proporcionalidade o número π:

A = πr²

4. Eficácia de um anúncio

Quanto mais eles vêem, mais eficaz um anúncio comercial. Eficácia e, em uma escala de 0 a 10, a partir de um aviso pode ser modelado de acordo com a seguinte função quadrática:

Referências 

1. Funções polinômicas. Recuperado de recursos.Educação.é.
2. Larson, r. (2012). Pré -cálculo. 8º. edição. Cengage Learning.
3. Miller, c. (2013). Matemática: Raciocínio e Aplicações. 12º. edição. Pearson Education.
4. Stewart, J. (2012). Pré -cálculo. Matemática para cálculo. 6º. edição. Cengage Learning.
5. Zill, d. (2008). Preccultment com avanços de cálculo. 4º. edição. McGraw Hill.