Equações fracionárias
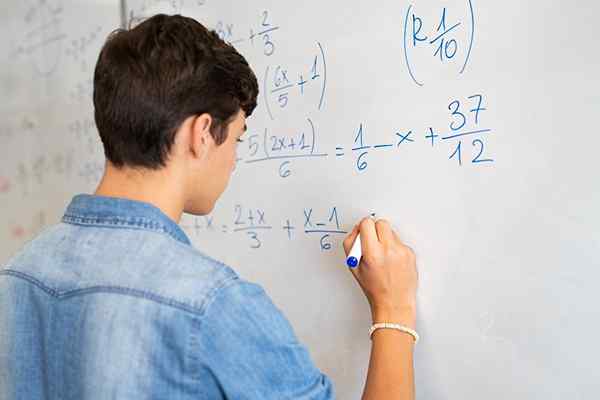
- 3931
- 276
- Gilbert Franecki
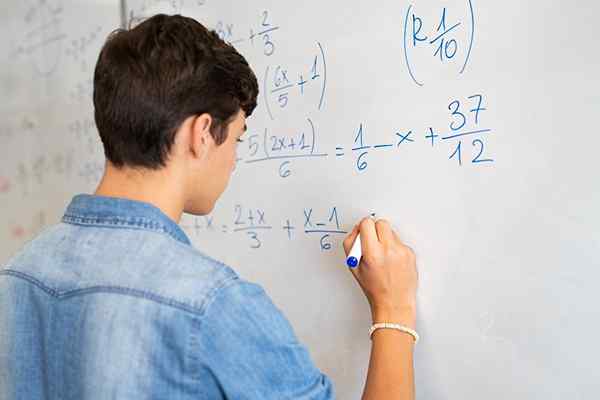 As equações fracionárias incluem frações numéricas e/ou algébricas, e o desconhecido pode estar no numerador e no denominador, ou ambos
As equações fracionárias incluem frações numéricas e/ou algébricas, e o desconhecido pode estar no numerador e no denominador, ou ambos O que são equações fracionárias?
As equações fracionárias são aqueles que contêm frações em um ou mais de seus termos. Tais frações podem ser numéricas ou algébricas, onde o desconhecido pode ser encontrado no numerador e/ou no denominador de qualquer termo.
Então, alguns exemplos de equações fracionárias com um único desconhecido:
O primeiro exemplo é uma equação linear com coeficientes fracionários; No segundo exemplo, o desconhecido está no denominador de cada um dos termos e, no último, o desconhecido é o numerador e no denominador.
Para resolvê -los, é necessário realizar algumas transformações algébricas e, assim, obter uma equação equivalente, na qual o desconhecido não aparece no denominador. Depois que este procedimento é realizado, a solução é encontrada usando as técnicas apropriadas.
A solução consiste no conjunto de valores "x" que atendem à igualdade. Pode ser um valor único, ou vários, mas, em qualquer caso, é muito importante ter em mente que nem todas as soluções na equação equivalente são aceitáveis para a equação original.
De fato, se é uma equação cujo desconhecido está no denominador, os valores "x" que anulam deve ser evitado, mesmo que pertencem ao conjunto de soluções equivalentes equivalentes. Isso ocorre porque a divisão entre 0 não está definida.
Se a equação equivalente tiver uma solução única, e acontece que o denominador de qualquer um dos termos da equação original é cancelado, então ela não tem solução.
Como resolver uma equação fracionária
As operações que são realizadas para resolver equações não confrativas são válidas, desde que a igualdade seja mantida. Dessa maneira, em uma equação fracionária, você pode adicionar ou subtrair a mesma quantidade a ambos os lados da igualdade, multiplicar todos os termos pela mesma quantidade ou dividir cada termo pela mesma quantidade (diferente de 0).
Pode servir você: Teorema de BolzanoMas como a equação fracionária é necessária para se transformar em outro equivalente sem denominadores, as seguintes indicações gerais também são seguidas:
- Encontre o múltiplo comum mínimo de denominadores (M.c.m).
- Multiplique cada termo pelo M.c.m., Para eliminar os denominadores.
- Resolva a equação equivalente obtida.
- Verifique se as soluções encontradas satisfazem a igualdade original.
Tipos de equações equivalentes
As equações equivalentes obtidas após o procedimento indicado podem ser:
- Linear ou em primeiro grau
- Quadrático
- De ordem superior
Exemplos resolvidos
Exemplo 1
Resolva a seguinte equação:
Note -se que a equação é em primeiro grau em "X", pois "x" é alto em 1. Os coeficientes da equação são frações e uma maneira de eliminá -los, para trabalhar com números inteiros, multiplicando todos os termos pelo múltiplo mínimo de denominadores (M.c.m.).
m.c.m. (2,3,6) = 6
Então:
3x - 2x = 1
x = 1
O leitor pode verificar a validade desta solução, substituindo x = 1 na equação original e verificando que uma igualdade é obtida.
Exemplo 2
Determine os valores "x" que satisfazem:
Ao contrário do exemplo anterior, neste caso o desconhecido é encontrado no denominador. Observe que os denominadores são anulados para os valores x = 2 e x = −1, um detalhe que é conveniente para levar em consideração, pois, se a equação equivalente admite essas soluções, devemos descartá -los, pois eles não são admissíveis Na equação original.
Agora devemos transformar a equação em outra sem denominadores, o primeiro passo é fazer com que a soma dos termos à esquerda da igualdade:
Como os denominadores são iguais, de modo que a igualdade é cumprida, é necessário que os numeradores também sejam:
Pode atendê -lo: proporcionalidade constante: o que é, cálculo, exercícios4 (x+1) - 3 (x -2) = 8
Basta resolver esta equação, que acaba sendo a primeira série:
4x + 4 - 3x + 6 = 8
x = 8 - 6 - 4 = - 2
x = - 2
Como esse valor é diferente dos valores proibidos, é admitido como uma solução da equação original.
Exemplo 3
Encontre a solução de:
Nesta equação, o valor x = 4 cancela os denominadores, portanto, é excluído do conjunto de soluções da equação transformada, se aparecer.
A equação transformada é fácil de encontrar, basta multiplicar todos os termos pelo fator (X-4):
Ficando:
2x - 4 = 4
2x = 8
x = 4
Exemplo 4
Resolva a equação:
Nesse caso, os denominadores têm termos quadráticos, por isso é conveniente fatorá -los primeiro:
- x2 + 8x + 7 = (x + 7) (x + 1)
- x2 - 49 = (x + 7) (x - 7)
- x2 - 6x - 7 = (x - 7) (x + 1)
A equação é assim:
Os valores de x que cancelam qualquer um dos denominadores são: x = −7, x = 7, x = −1. Portanto, mesmo que esses valores façam parte do conjunto de soluções da equação modificada, eles não podem ser uma solução da equação original.
Agora vem o processo de transformar a equação. O primeiro passo é encontrar o múltiplo comum mínimo dos denominadores:
m.c.m. = (x + 7) (x - 7) (x + 1)
Multiplicando em ambos os lados da igualdade por M.c.m. é sobrou:
Resultante:
(x --7) (x− 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)
Através da propriedade distributiva, os produtos são desenvolvidos:
x2 - 9x +14 = 2x2 - 3x - 5 - (x2 + 5x - 14)
Reduzindo termos semelhantes no lado direito:
x2 - 9x + 14 = x2 - 8x + 9
Os termos quadráticos são cancelados, encontrando o mesmo sinal em diferentes lados da igualdade:
Pode servir a você: diferença de cubos: fórmulas, equações, exemplos, exercícios- 9x + 14 = - 8x + 9
-x = -5 ⇒ x = 5
Este resultado é admitido como uma solução, pois não é nenhum dos valores proibidos.
Exercício de aplicação de equações fracionárias
O denominador de uma fração excede quatro unidades ao numerador. Se o numerador for subtraído do numerador e o denominador também, a fração resultante é 3/5. Determine a fração original.
Solução
Seja x o valor do numerador.
Como o denominador da fração excede quatro unidades ao numerador, a fração original é:
Agora você precisa subtrair 5 unidades, tanto para o numerador quanto o denominador:
Como a fração resultante da realização do procedimento anterior é igual a 3/5, eles são equalizados:
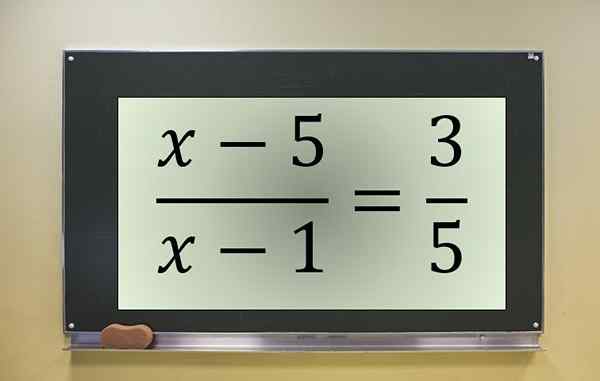 Exemplo de equação fracionária. Fonte: f. Zapata.
Exemplo de equação fracionária. Fonte: f. Zapata. Esta é uma equação fracionária com o desconhecido em numerador e denominador, que é cancelado em x = 1. Portanto, esse valor deve ser excluído, se estivesse entre as soluções da equação transformada.
Em seguida, ele multiplica os dois lados pelo múltiplo comum mínimo, que é 5 (x - 1):
Resultando na seguinte equação equivalente:
5 (x - 5) = 3 (x - 1)
Aplicando propriedade distributiva:
5x -25 = 3x - 3 ⇒ 2x = 22
x = 11
A fração original está substituindo x = 11 na expressão:
Resultando em fração 11/15. Esta é a resposta para o problema levantado.
Referências
- Equações fracionárias. Recuperado de: Mathepower.com
- Portal de Matemática. Equações fracionárias. Resolução de problemas. Recuperado de: Silvioduarte.com.
- Stewart, J. (2007). Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
- Sullivan, m. (1997). Pré -cálculo. 4º. Edição. Pearson Education.
- Zill, d. (2008). Preccultment com avanços de cálculo. 4º. Edição. McGraw Hill.



(x+1))

=6\left%20(%20\frac16%20\right%20))
-3(x-2)(x-2)(x+1)=\frac8(x-2)(x+1))
\left%20(%20\fracxx-4%20\right%20)+(x-4)=(x-4)\left%20(%20\frac4x-4%20\right%20))

(x+1)=\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1))
(x-7)(x+1)\left%20[%20\fracx-2(x+7)(x+1)%20\right%20]=(x+7)(x-7)(x+1)\left%20[%20\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1)%20\right%20])



\left%20(%20\fracx-5x-1%20\right%20)=5(x-1)\frac35)